安徽省淮南市八公山区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-14 类型：期末考试

进入出卷网下载

一、单选题

1. 已知点P（x+3，x﹣4）在x轴上，则x的值为（）

A、3 B、4 C、﹣3 D、﹣4

查看试题解析
2. 点A₁（5， –7）关于x轴对称的点A₂的坐标为（）

A、（–5, –7） B、（–7 ，–5） C、（5，7） D、（7， –5）

查看试题解析
3. 下列各数中最小的数是 $($ $)$

A、 $- π$ B、 $- 3$ C、 $- \sqrt{5}$ D、0

查看试题解析
4. 已知a＞b，则下列不等式一定成立的是（）

A、a＋4＜b＋4 B、2a＜2b C、－2a＜－2b D、a－b＜0

查看试题解析
5. 已知不等式组 ${\begin{matrix} x > 3 \\ x > m \end{matrix}$ 的解集为x＞3，则m的取值范围是（）

A、m＝3 B、m＞3 C、m≥3 D、m≤3

查看试题解析
6. 二元一次方程x+y=5的正整数解有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是方程组 ${\begin{cases} a x + b y = 5 \\ b x + a y = 1 \end{cases}$ 的解，则a﹣b的值是（）

A、 $- 1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
8. 今年我市有近4万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计解析，以下说法正确的是（）

A、这1000名考生是总体的一个样本 B、近4万名考生是总体 C、每位考生的数学成绩是个体 D、1000名学生是样本容量

查看试题解析
9. 不等式ax＋b＞0（a＜0）的解集是（）

A、x＞- $\frac{b}{a}$ B、x＜- $\frac{b}{a}$ C、x＞ $\frac{b}{a}$ D、x＜ $\frac{b}{a}$

查看试题解析
10. 已知点P（x，y），且 $| x - 2 | + | y + 4 | = 0$ ，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

二、填空题

11. 如果a＜b，那么﹣3a﹣3b（用“＞”或“＜”填空）．

查看试题解析
12. 甲乙两队进行篮球对抗赛，比赛规则规定每队胜一场得3分，平一场得1分，负一场得0分，两队一共比赛了10场，甲队保持不败，得分不低于24分，甲队至少胜了场.

查看试题解析
13. 已知点A（0，1），B（0 ，2），点C在x轴的正半轴上，且 $S_{Δ A B C} = 2$ ，则点C的坐标．

查看试题解析
14. 已知方程组 ${\begin{array}{l} 2 x + y = 3 \\ x - y = 6 \end{array}$ 的解满足方程x＋2y＝k，则k的值是.

查看试题解析
15. 如图，有一条平直的等宽纸带按图折叠时，则图中∠α=

查看试题解析
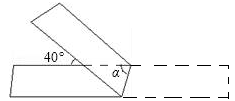16. 两个角的两边分别平行，一个角是50°，那么另一个角是.

查看试题解析

三、解答题

17. 解方程组 ${\begin{cases} 2 x + y = 4 ① \\ x + 2 y = 5 ② \end{cases}$

查看试题解析
18. 解不等式组： ${\begin{matrix} 2 (x - 1) \leq 3 x + 1 \\ \frac{x}{3} < \frac{x + 1}{4} \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
19.
如图，将△ABC向右平移5个单位长度，再向下平移2个单位长度，得到△A′B′C′.

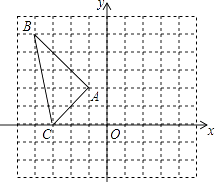(1)、请画出平移后的图形△A′B′C′；

(2)、并写出△A′B′C′各顶点的坐标；

(3)、求出△A′B′C′的面积．

查看试题解析
20. 观察下列两个等式： $2 - \frac{1}{3} = 2 \times \frac{1}{3} + 1$ ， $5 - \frac{2}{3} = 5 \times \frac{2}{3} + 1$ ，给出定义如下：我们称使等式 $a - b = a b + 1$ 成立的一对有理数 $a$ ， $b$ 为“共生有理数对”，记为（ $a$ ， $b$ ），如：数对（ $2$ ， $\frac{1}{3}$ ），（ $5$ ， $\frac{2}{3}$ ），都是“共生有理数对”．

(1)、判断数对（ $- 2$ ，1），（ $3$ ， $\frac{1}{2}$ ）是不是“共生有理数对”，写出过程；

(2)、若（ $a$ ， $3$ ）是“共生有理数对”，求 $a$ 的值；

查看试题解析
21. 大东方商场销售A、B两种品牌的钢琴，这两种钢琴的进价和售价如下表所示：

A

B

进价（万元/套）

1.5

1.2

售价（万元/套）

1.65

1.4

该商场计划购进两种钢琴若干套，共需66万元，全部销售后可获毛利润9万元．（毛利润＝（售价－进价）×销售量）求该商场计划购进A、B两种品牌的钢琴各多少套？

查看试题解析
22. 某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查（问卷调查表如右图所示），并将调查结果绘制成图 1 和图 2 所示的统计图（均不完整）．请根据统计图中提供的信息，解答下列问题：

(1)、本次接受调查的总人数是人．

(2)、请将条形统计图补充完整．

(3)、在扇形统计图中，观点E的百分比是，表示观点B的扇形的圆心角度为度．

查看试题解析

	A	B
进价（万元/套）	1.5	1.2
售价（万元/套）	1.65	1.4