陕西省商洛市2020-2021学年高二下学期理数期末考试试卷
试卷更新日期:2021-07-14 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 设集合 , ,则图中阴影部分表示的集合为( )
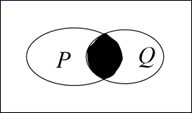 A、 B、 C、 D、3. 若函数 , ,则( )A、 为奇函数, 为偶函数 B、 与 均为偶函数 C、 为偶函数, 为奇函数 D、 与 均为奇函数4. 设平面 与平面 的交线为 ,则“ 内存在直线 ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 曲线 在点 处切线的斜率为( )A、 B、 C、 D、6. 展开式中的第5项为常数项,则正整数n的值为( )A、2 B、3 C、4 D、57. 不等式组 ,表示的平面区域的面积为( )A、2 B、3 C、4 D、58. 设四面体 的每个顶点都在球 的球面上, 平面 , ,且 , ,则球 的表面积为( )A、 B、 C、 D、9. 设某车间的A类零件的质量m(单位: )服从正态分布 ,且 .若从A类零件中随机选取100个,则零件质量在 的个数大约为( )A、40 B、30 C、60 D、2410. 已知 为曲线 上一点, , ,则 的最小值为( )A、6 B、 C、5 D、11. 已知函数 在 上恰有6个零点,则 的取值范围是( )A、 B、 C、 D、12. 若 , , ,则( )A、 B、 C、 D、
A、 B、 C、 D、3. 若函数 , ,则( )A、 为奇函数, 为偶函数 B、 与 均为偶函数 C、 为偶函数, 为奇函数 D、 与 均为奇函数4. 设平面 与平面 的交线为 ,则“ 内存在直线 ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 曲线 在点 处切线的斜率为( )A、 B、 C、 D、6. 展开式中的第5项为常数项,则正整数n的值为( )A、2 B、3 C、4 D、57. 不等式组 ,表示的平面区域的面积为( )A、2 B、3 C、4 D、58. 设四面体 的每个顶点都在球 的球面上, 平面 , ,且 , ,则球 的表面积为( )A、 B、 C、 D、9. 设某车间的A类零件的质量m(单位: )服从正态分布 ,且 .若从A类零件中随机选取100个,则零件质量在 的个数大约为( )A、40 B、30 C、60 D、2410. 已知 为曲线 上一点, , ,则 的最小值为( )A、6 B、 C、5 D、11. 已知函数 在 上恰有6个零点,则 的取值范围是( )A、 B、 C、 D、12. 若 , , ,则( )A、 B、 C、 D、二、填空题
-
13. 圆 的圆心到直线 的距离为.14. 已知向量 与 垂直,则 .15. 已知 的内角A , B , C的对边分别为a , b , c , 且 ,现有下列四个结论:① ;②当 , 时, ;③当 时, 外接圆的面积为 ;④当 时, 面积的最大值为 .其中所有正确结论的编号是.16. 中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器.如图,某沙漏由上、下两个圆锥容器组成,圆锥底面圆的直径和高均为4cm,当细沙全部在上部时,其高度为圆锥高度的 (细管长度忽略不计).若细沙的流速为每分钟1cm3 , 则上部细沙全部流完的时间约为分钟(结果精确到整数部分);若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则该沙堆的高为cm.

三、解答题
-
17. 如图,在空间直角坐标系 中,A , D , B分别在x , y , z轴的正半轴上,C在平面BOD内.
 (1)、若 ,证明: .(2)、已知 , ,C的坐标为 ,求BC与平面ACD所成角的正弦值.18. 2020年某地苹果出现滞销现象,为了帮助当地果农度过销售难关,当地政府与全国一些企业采用团购的方式带动销售链,使得积压了许多苹果的当地果农有了销路.为了解果农们苹果的销售量情况,当地农业局随机对100名果农的苹果销售量进行统计,将数据分成 , , , 4组,得到如图所示的频率分布直方图.(同一组中的每个数据可用该组区间的中点值代替)
(1)、若 ,证明: .(2)、已知 , ,C的坐标为 ,求BC与平面ACD所成角的正弦值.18. 2020年某地苹果出现滞销现象,为了帮助当地果农度过销售难关,当地政府与全国一些企业采用团购的方式带动销售链,使得积压了许多苹果的当地果农有了销路.为了解果农们苹果的销售量情况,当地农业局随机对100名果农的苹果销售量进行统计,将数据分成 , , , 4组,得到如图所示的频率分布直方图.(同一组中的每个数据可用该组区间的中点值代替) (1)、试估计这100名果农苹果销售量的平均数;(2)、假设这100名果农在未打开销路之前都积压了2万千克的苹果,通过团购的方式果农每千克苹果的纯利润为1.3元,而积压仍未售出的苹果每千克将损失2元的成本费,试估计这100名果农积压的苹果通过此次团购活动获得的总利润.19. 在各项均为正整数的等差数列 中, ,且 为小于10的质数.(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .20. 已知椭圆 的焦点与双曲线 的焦点相同,且D的离心率为 .(1)、求C与D的方程;(2)、若 ,直线 与C交于A , B两点,且直线PA , PB的斜率都存在.
(1)、试估计这100名果农苹果销售量的平均数;(2)、假设这100名果农在未打开销路之前都积压了2万千克的苹果,通过团购的方式果农每千克苹果的纯利润为1.3元,而积压仍未售出的苹果每千克将损失2元的成本费,试估计这100名果农积压的苹果通过此次团购活动获得的总利润.19. 在各项均为正整数的等差数列 中, ,且 为小于10的质数.(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .20. 已知椭圆 的焦点与双曲线 的焦点相同,且D的离心率为 .(1)、求C与D的方程;(2)、若 ,直线 与C交于A , B两点,且直线PA , PB的斜率都存在.①求m的取值范围.
②试问这直线PA , PB的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.