安徽省阜阳市颍州区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-07-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，是有理数的为（　　）

A、 $\sqrt{2}$ B、 $\sqrt[3]{4}$ C、π D、0

查看试题解析
2. 若 $a > b$ ，则下列各式中一定成立的是（）

A、 $a - 2 < b - 2$ B、 $a c^{2} > b c^{2}$ C、 $- 2 a > - 2 b$ D、 $a + 2 > b + 2$

查看试题解析
3. 下列调查中，适宜采用普查方式的是（）

A、调查乘坐飞机的旅客是否携带了违禁物品 B、调查某品牌圆珠笔芯的使用寿命 C、调查冷饮市场上冰淇淋的质量情况 D、调查全国中学生心理健康现状

查看试题解析
4. 已知点P（1﹣2a，a+3）在第二象限，则a的取值范围是（）

A、a＜﹣3 B、a＞ $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ ＜a＜3 D、﹣3＜a＜ $\frac{1}{2}$

查看试题解析
5. 将直尺和直角三角板按如图方式摆放（∠ACB为直角），已知∠1=30°，则∠2的大小是（）

A、30° B、45° C、60° D、65°

查看试题解析
6. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠D＝∠DCE D、∠D＋∠ACD＝180°

查看试题解析
7. 甲、乙两地相距360千米，一轮船往返于甲、乙两地之间，顺水行船用18小时，逆水行船用24小时，若设船在静水中的速度为x千米/时，水流速度为y千米/时，则下列方程组中正确的是(　　)

A、 ${\begin{array}{l} 18 (x + y) = 360 \\ 24 (x - y) = 360 \end{array}$ B、 ${\begin{array}{l} 18 (x + y) = 360 \\ 24 (x + y) = 360 \end{array}$ C、 ${\begin{array}{l} 18 (x - y) = 360 \\ 24 (x - y) = 360 \end{array}$ D、 ${\begin{array}{l} 18 (x - y) = 360 \\ 24 (x + y) = 360 \end{array}$

查看试题解析
8. 关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 2 y = a, \\ 2 x + y = 2 a - 6 \end{array}$ 的解满足 $x + y = 0$ ，则 $a$ 的值为（）

A、8 B、6 C、4 D、2

查看试题解析
9. 为了了解某校七年级学生的体能情况，随机调查了其中100名学生，测试学生在1分钟内跳绳的次数，并绘制成如图所示的频数分布直方图，请根据图形计算，跳绳次数（ $x$ ）在 $120 < x < 200$ 范围内人数占抽查学生总人数的百分比为（）

A、43% B、50% C、57% D、73%

查看试题解析
10. 在平面直角坐标系xOy中，对于点P（x，y），我们把点 $P^{'} (- y + 1 ， x + 1)$ 叫做点P的伴随点．已知点 $A_{1}$ 的伴随点为 $A_{2}$ ，点 $A_{2}$ 的伴随点为 $A_{3}$ ，点 $A_{3}$ 的伴随点为 $A_{4}$ ，…，这样依次得到点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ，…， $A_{n}$ ．若点 $A_{1}$ 的坐标为（3，1），则点 $A_{2021}$ 的坐标为（）

A、（0，－2） B、（0，4） C、（3，1） D、（－3，1）

查看试题解析

二、填空题

11. $\sqrt{16}$ 的平方根是．

查看试题解析
12. 在平面直角坐标系中，点A（－2，5），AB $//$ x轴，AB＝3，则点B的坐标是．

查看试题解析
13. 若 $\sqrt{x + 2 y - 6} + {(2 x + y + 3)}^{2} = 0$ ，则 $x + y$ 的值为．

查看试题解析
14. 如图，把直角梯形ABCD沿AD方向平移到梯形EFGH的位置，HG＝24cm，MG＝6cm，MC＝4cm，则阴影部分的面积是cm² ．

查看试题解析

三、解答题

15. 计算： $- 1^{2} + | \sqrt{3} - 2 | - \sqrt[3]{- 27} \times (- \sqrt{\frac{1}{9}})$

查看试题解析
16. 解方程组．

(1)、 ${\begin{array}{l} x = y + 1 \\ 3 x - 2 y = 2 \end{array}$

(2)、 ${\begin{array}{l} 4 x - 2 y = 2 \\ 3 x + 2 y = 5 \end{array}$

查看试题解析
17. 解不等式组 ${\begin{array}{l} x + 1 ⩽ 3 \\ x - 1 < 4 (x + 2) \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
18. 如图，直线 $a / / b$ ，射线 $D F$ 与直线a相交于点C，过点D作 $D E ⊥ b$ 于点E，已知 $∠ 1 = 25 °$ ，求 $∠ 2$ 的度数.

查看试题解析
19. 如图所示，三角形ABC（记作△ABC）在方格中，方格纸中的每个小方格都是边长为1个单位的正方形，三个顶点的坐标分别是A（－2，1），B（－3，－2），C（1，－2），先将△ABC向上平移3个单位长度，再向右平移2个单位长度，得到A₁B₁C₁.

(1)、在图中画出△A₁B₁C₁；

(2)、点A₁ ， B₁ ， C₁的坐标分别为、、；

(3)、若y轴有一点P，使△PBC与△ABC面积相等，求出P点的坐标.

查看试题解析
20. 甲、乙两人共同解方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x + b y = - 2 ② \end{array}$ ，解题时由于甲看错了方程①中的a，得到方组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ；乙看错了方程②中的b，得到方程组的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，试计算 $a^{2020} + {(- \frac{1}{10} b)}^{2021}$ 的值．

查看试题解析
21.
某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．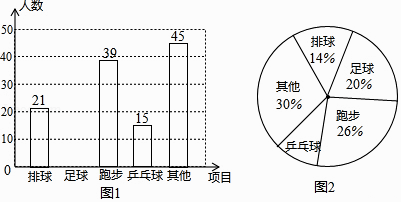
请结合以上信息解答下列问题：

(1)、m=；

(2)、请补全上面的条形统计图；

(3)、在图2中，“乒乓球”所对应扇形的圆心角的度数为；

(4)、已知该校共有1200名学生，请你估计该校约有名学生最喜爱足球活动．

查看试题解析
22. 如图，点D、F在线段AB上，点E、G分别在线段BC和AC上，CD $//$ EF，∠1＝∠2．

(1)、判断DG与BC的位置关系，并说明理由；

(2)、若DG是∠ADC的平分线，∠3＝85°，且∠DCE∶∠DCG＝9∶10，试说明AB与CD有怎样的位置关系？

查看试题解析
23. “一方有难，八方支援”，某公司准备向灾区捐赠一批帐篷和食品包共360个，其中帐篷比食品包多120个．

(1)、求帐篷和食品包各有多少个？

(2)、该公司准备一次性将这批帐篷和食品包运往灾区，现计划租用甲、乙两种型号的货车共8辆，已知每辆甲种型号的货车最多可装45个帐篷和10个食品包，每辆乙种型号的货车最多可装25个帐篷和20个食品包，运输部门安排甲、乙两种型号的货车时，有几种方案？请你帮助设计出来．

(3)、在（2）的条件下，如果甲种型号的货车每辆需付运费1000元，乙种型号的货车每辆需付运费900元．假设你是决策者，应选择哪种方案可使运费最少？最少运费是多少元？

查看试题解析