湖北省新高考联考协作体2020-2021学年高二下学期数学期末考试试卷

试卷更新日期：2021-07-14 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\frac{1 + a i}{2 - i}$ 为实数，其中i为虚数单位，则实数a的值为（）

A、2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、-2

查看试题解析
2. 已知函数 $y = \lg (- x^{2} - x + 2)$ 的定义域为集合M，函数 $y = \sin x$ 的值域为N，则 $M \cap N =$ （）

A、 $\emptyset$ B、 $(- 2, 1]$ C、 $[- 1, 1)$ D、 $[- 1, 1]$

查看试题解析
3. 函数 $f (x) = \frac{2 x^{\frac{5}{3}}}{\ln | x |}$ 在其定义域上的图象大致为（）

A、 B、 C、 D、

查看试题解析
4. 一次竞赛考试，老师让学生甲､乙､丙､丁预测他们的名次.学生甲说：丁第一；学生乙说：我不是第一；学生丙说：甲第一；学生丁说：甲第二.若有且仅有一名学生预测错误，则该学生是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

5. 某词汇研究机构为对某城市人们使用流行语的情况进行调查，随机抽取了200人进行调查统计得下方的

2 \times 2

列联表.则根据列联表可知（）

	年轻人	非年轻人	总计
经常用流行语	125	25	150
不常用流行用语	35	15	50
总计	160	40	200

参考公式：独立性检验统计量 $X^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .

下面的临界值表供参考：

P（x²≥x₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
x₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

A、有95%的把握认为“经常用流行用语”与“年轻人”有关系 B、没有95%的把握认为“经常用流行用语”与“年轻人”有关系 C、有97.5%的把握认为“经常用流行用语”与“年轻人”有关系 D、有97.5%的把握认为“经常用流行用语”与“年轻人”没有关系

查看试题解析

6. 某班将5名同学分配到甲、乙、丙三个社区参加劳动锻炼，每个社区至少分配一名同学，则甲社区恰好分配2名同学共有（）种不同的方法．

A、30 B、48 C、120 D、60

查看试题解析
7. 已知函数 $f (x) = {\begin{array}{l} 2 + 3 \ln x ， x \geq 1 \\ x + 1 ， x < 1 \end{array}$ ，若 $m \neq n$ ，且 $f (m) + f (n) = 4$ ，则 $m + n$ 的最小值是（）

A、2 B、 $e - 1$ C、 $4 - 3 \ln 3$ D、 $3 - 3 \ln 2$

查看试题解析
8. 设 $F_{1} ， F_{2}$ 分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点，圆 $F_{1}$ 与双曲线的渐近线相切，过 $F_{2}$ 与圆 $F_{1}$ 相切的直线与双曲线的一条渐近线垂直，则双曲线的两条渐近线所成的锐角 $α$ 的正切值为（）

A、 $\frac{8}{15}$ B、 $\sqrt{3}$ C、 $\frac{4}{3}$ D、1

查看试题解析

二、多选题

9. 下列命题正确的有（）

A、若随机变量 $X$ 服从正态分布 $N (1 ， δ^{2})$ ， $P (X \leq 4) = 0.79$ ，则 $P (X \leq - 2) = 0.21$ ． B、若随机变量 $X$ 服从二项分布： $X ~ B (4 ， \frac{1}{4})$ ，则 $D (2 X + 3) = 3$ ． C、若相关指数 $R^{2}$ 的值越趋近于0，表示回归模型的拟合效果越好 D、若相关系数 $r$ 的绝对值越接近于1，表示相关性越强．

查看试题解析
10. 下列选项中，关于x的不等式 $a x^{2} + (a - 1) x - 2 > 0$ 有实数解的充分不必要条件的有（）

A、 $a = 0$ B、 $a \geq - 3 + 2 \sqrt{2}$ C、 $a > 0$ D、 $a \leq - 3 - 2 \sqrt{2}$

查看试题解析
11. 已知函数 $f (x) = \log_{2} (1 + 4^{x}) - x$ ，则下列说法正确的是（）

A、函数 $f (x)$ 是偶函数 B、函数 $f (x)$ 是奇函数 C、函数 $f (x)$ 在 $(- \infty ， 0]$ 上为增函数 D、函数 $f (x)$ 的值域为 $[1 ， + \infty)$

查看试题解析
12. 已知球 $O$ 是正三棱锥(底面为正三角形，点在底面的射影为底面中心) $A - B C D$ 的外接球， $B C = 3$ ， $A B = 2 \sqrt{3}$ ，点 $E$ 在线段 $B D$ 上，且 $B D = 6 B E$ ，过点 $E$ 作球 $O$ 的截面，则所得截面圆的面积可能是（）

A、π B、2π C、3π D、4π

查看试题解析

三、填空题

13. ${(x - \frac{2}{\sqrt{x}})}^{6}$ 展开式中常数项为.

查看试题解析
14. 已知点 $P$ 在抛物线 $x^{2} = 4 y$ 上运动， $F$ 为抛物线的焦点，点 $A$ 的坐标为 $(2 ， 3)$ ，则 $P A + P F$ 的最小值为．

查看试题解析
15. 已知 $x$ ， $y$ ， $z$ 是正数，且 $11 x = 13 y = 15 z$ ，则 $11^{x}$ ， $13^{y}$ ， $15^{z}$ 的大小关系为（用“>”联结）．

查看试题解析
16. 罗默､伯努利家族､莱布尼兹等大数学家都先后研究过星形线 $C : x^{\frac{2}{3}} + y^{\frac{2}{3}} = 1$ 的性质，其形美观，常用于超轻材料的设计.曲线C围成的图形的面积S2（选填“>”､“<”或“=”），曲线C上的动点到原点的距离的取值范围是.

查看试题解析

四、解答题

17. 求函数 $f (x) = \frac{1}{3} x^{3} + \frac{1}{2} x^{2} - 2 x + \frac{8}{3}$ 在区间 $x \in [- 3 ， 3]$ 上的最大值和最小值．

查看试题解析
18. 为了树立和践行绿水青山就是金山银山的理念，加强环境的治理和生态的修复，某市在其辖区内某一个县的27个行政村中各随机选择农田土壤样本一份，对样本中的铅、锦、铭等重金属的含量进行了检测，并按照国家土壤重金属污染评价级标准（清洁、尚清洁、轻度污染、中度污染、重度污染）进行分级，绘制了如图所示的条形图

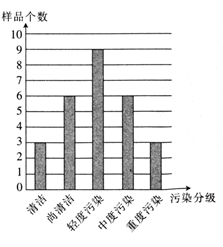(1)、从轻度污染以上（包括轻度污染）的行政村中按分层抽样的方法抽取6个，求在轻度、中度、重度污染的行政村中分别抽取的个数；

(2)、规定：轻度污染记污染度为1，中度污染记污染度为2，重度污染记污染度为3．从（1）中抽取的6个行政村中任选3个，污染度的得分之和记为X ，求X的数学期望．

查看试题解析
19. 如图，在五面体 $A B C D E F$ 中，四边形 $A B E F$ 为正方形，平面 $A B E F ⊥$ 平面 $C D F E$ ， $C D / / E F$ ， $D F ⊥ E F$ ， $E F = 2 C D = 2$ .

(1)、若 $D F = 2$ ，求二面角 $A - C E - F$ 的正弦值；

(2)、若平面 $A C F ⊥$ 平面 $B C E$ ，求 $D F$ 的长.

查看试题解析

20. 某新建工厂落成后，开工后的前5个月的利润情况如下表所示：

	第1个月	第2个月	第3个月	第4个月	第5个月
利润（单位：万元）	1	11	27	51	80

设第 $t$ 个月的利润为 $y$ 万元．

(1)、根据表中数据，求

y

关于

t

的回归方程

\hat{y} = \hat{b} {(t - 1)}^{2} + \hat{a}

：（注：

\hat{a}

，

\hat{b}

的值要求保留小数点后两位有效数字）

(2)、根据已知数据求得回归方程后，为验证该方程的可靠性，可用一个新数据加以验证，方法如下：先计算新数据

(x_{0} ， y_{0})

对应的残差

ξ_{0} (ξ_{0} = y_{0} - \hat{y})

，再计算

| \frac{ξ_{0}}{y_{0}} |

，若

| \frac{ξ_{0}}{y_{0}} | < 0.05

，则说明该方程是可靠的，否则说明不可靠．现已知该厂第6个月的利润为120万元，试判断（1）中求得的回归方程是否可靠，说明你的理由．

参考数据： $1^{4} + 2^{4} + 3^{4} + 4^{4} = 354$ ，取 $\frac{419}{87} = 4.82$ ．

回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘法估计公式分别为： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

查看试题解析

21. 已知点 $F (1 ， 0)$ ，直线 $l$ ： $x = 2$ ，动点 $P$ 满足到点 $F$ 的距离与到直线 $1$ 的距离之比为 $\frac{\sqrt{2}}{2}$ ．

(1)、求动点 $P$ 的轨迹 $E$ 的方程．

(2)、经过点 $(2 ， 0)$ 的直线与曲线 $E$ 交于 $A$ ， $B$ 两点，直线 $A F$ 、 $B F$ 的斜率分别为 $k_{1}$ ， $k_{2} (k_{2} \neq 0)$ ，求证： $\frac{k_{1}}{k_{2}}$ 为定值．

查看试题解析
22. 已知函数 $f (x) = (x + m) e^{x}$

(1)、若 $f (x)$ 在 $(- \infty ， 1]$ 上是减函数，求实数m的取值范围；

(2)、当 $m = 0$ 时，若对任意的 $x \in (0 ， + \infty)$ ， $n x \ln (n x) \leq f (2 x)$ 恒成立，求实数n的取值范围．

查看试题解析