湖北省2020-2021学年高二下学期数学7月期末考试试卷
试卷更新日期:2021-07-14 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、2 D、82. 命题“ , ”的否定为( )A、 , B、 , C、 , D、 ,3. 曲线 在点 处的切线方程是( )A、 B、 C、 D、4. 若点 在圆 的外部,则实数 的取值范围是( )A、 B、 C、 D、5. 我国古代数学名著《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.在如图所示的“堑堵”中, ,则二面角 的正切值为( )
 A、1 B、2 C、 D、6. 已知随机变量 ,正数 , 满足 ,则 的最小值为( )A、2 B、 C、4 D、97. 某校为了了解学生性别与对篮球运动的态度(喜欢或不喜欢),随机抽取部分同学进行了一次调查,其中被调查的男生和女生人数相同,得到如图所示的等高条形统计图,若有超过99%的把握认为性别与对篮球运动的态度有关,则被调查的总人数可能为( )
A、1 B、2 C、 D、6. 已知随机变量 ,正数 , 满足 ,则 的最小值为( )A、2 B、 C、4 D、97. 某校为了了解学生性别与对篮球运动的态度(喜欢或不喜欢),随机抽取部分同学进行了一次调查,其中被调查的男生和女生人数相同,得到如图所示的等高条形统计图,若有超过99%的把握认为性别与对篮球运动的态度有关,则被调查的总人数可能为( )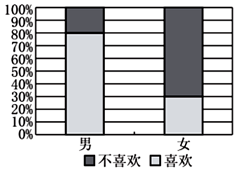
附: ,其中 .
P(K2≥k)
0.010
0.001
k
6.635
10.828
A、100 B、120 C、145 D、1608. 已知 , 为正数, ,则下列不等式一定成立的是( )A、 B、 C、 D、二、多选题
-
9. 下列函数是奇函数的是( )A、 B、 C、 D、10. 关于二项式 的展开式,下列结论正确的是( )A、各项二项式系数之和为 B、各项系数之和为1 C、只有第5项的二项式系数最大 D、常数项为67211. 已知函数 满足:① 的图象关于点 对称;② 的图象关于直线 对称;③方程 在 上至多有2个实数根,则 的值可以是( )A、2 B、8 C、10 D、1812. 已知双曲线 的离心率为2,点 , 是 上关于原点对称的两点,点 是 的右支上位于第一象限的动点(不与点 、 重合),记直线 , 的斜率分别为 , ,则下列结论正确的是( )A、以线段 为直径的圆与 可能有两条公切线 B、 C、存在点 ,使得 D、当 时,点 到 的两条渐近线的距离之积为3
三、填空题
-
13. 在平行六面体 中, 是线段 的中点,若 ,则 .14. 已知抛物线 的焦点为 ,过点 的直线 与 交于 , 两点,若 为坐标原点, 的重心为点 ,则 .15. 为了缓解早高峰期的交通压力,社区安排5名志愿者到3个路口协助交警维持交通秩序,每人只到1个路口,每个路口至少安排1人,则不同的安排方法总数是 . (用数字作答)16. 在 中,内角 , , 所对的边分别为 , , ,已知 , ,且 ,则 的面积 ;若 ,则 的值为 .
四、解答题
-
17. 已知数列 的前 项和 ,且满足: , .(1)、求数列 的通项公式;(2)、若 ,求数列 的前 项和 .18. 已知函数 ,其中 .(1)、当 时,求 的极值;(2)、当 时,求 的零点个数.19. 最近,新冠疫苗接种迎来高峰,市民在当地医院即可免费接种,根据国家卫生健康委员会的数据,我国总接种量排名世界第一,有望早日建立起全民免疫屏障.某医院抽取部分已接种疫苗的市民进行统计调查,将年龄按 , , , 分组,得到如图所示的频率分布直方图.
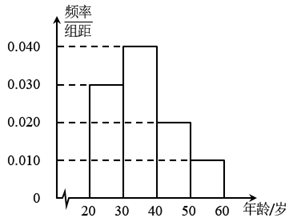 (1)、求图中市民年龄的平均数(同一组中的数据用该组区间的中点值作代表);(2)、以频率估计概率,若从当地所有的已接种市民中随机抽取3人进行电话回访,记其中年龄在 的人数为 ,求 的分布列和数学期望.
(1)、求图中市民年龄的平均数(同一组中的数据用该组区间的中点值作代表);(2)、以频率估计概率,若从当地所有的已接种市民中随机抽取3人进行电话回访,记其中年龄在 的人数为 ,求 的分布列和数学期望.

