河北省邢台市信都区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-13 类型:期末考试
一、选择题
-
1. 在函数 中, 的值为( )A、-5 B、2 C、5 D、-22. 在平面直角坐标系中,下面的点在第二象限的是( )A、 B、 C、 D、3. 某市为了解870万市民的出行情况,科学规划轨道交通,500名志愿者走入1万户家庭,发放并收回了4万份问卷,进行调查登记.该调查中的样本容量是( )A、870万 B、500 C、1万 D、4万4. 如图,在 中, 、 分别是 、 边上的中点,若 ,则 等于( )
 A、2 B、4 C、8 D、105. 如图的四个选项中,函数 的图象大致是( )A、
A、2 B、4 C、8 D、105. 如图的四个选项中,函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 6. 某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )A、在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测 B、随意调查10名老年人是否参与了新冠病毒核酸和抗体检测 C、在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测 D、利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测7. 已知直线 与 相交于点 ,则关于 , 的二元一次方程组 的解为( )A、 B、 C、 D、8. 在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( )A、(3,8) B、(1,8) C、(1,4) D、(3,4)9. 下列不能表示 是 的函数的是( )A、
6. 某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )A、在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测 B、随意调查10名老年人是否参与了新冠病毒核酸和抗体检测 C、在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测 D、利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测7. 已知直线 与 相交于点 ,则关于 , 的二元一次方程组 的解为( )A、 B、 C、 D、8. 在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( )A、(3,8) B、(1,8) C、(1,4) D、(3,4)9. 下列不能表示 是 的函数的是( )A、
B、0
5
10
15
3
3.5
4
4.5
 C、
C、 D、
D、1
3
5
7
2
-1
4
0.2
10. 如图,若棋子“炮”的坐标为 ,棋子“马”的坐标为 ,则棋子“车”的坐标为( ) A、 B、 C、 D、11. 如图,矩形 中,对角线 , 相交于点 ,若 ,则 ( )
A、 B、 C、 D、11. 如图,矩形 中,对角线 , 相交于点 ,若 ,则 ( ) A、20° B、40° C、80° D、100°12. 如图,表示的是某中学九(3)班学生外出方式(乘车、步行、骑车)的条形统计图(部分)和扇形分布图,那么下列说法正确的是( )
A、20° B、40° C、80° D、100°12. 如图,表示的是某中学九(3)班学生外出方式(乘车、步行、骑车)的条形统计图(部分)和扇形分布图,那么下列说法正确的是( )
 A、九(3)班外出的学生共有42人 B、九(3)班外出步行的学生有8人 C、在扇形图中,步行的学生人数所占的圆心角为82° D、如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人13. 已知 , , , ,若 ,且 ,则 的值可能是( )A、3 B、6 C、9 D、1214. 将图1中两个三角形按图2所示的方式摆放,其中四边形 为矩形,分别连接 、 .甲、乙两人有如下结论:
A、九(3)班外出的学生共有42人 B、九(3)班外出步行的学生有8人 C、在扇形图中,步行的学生人数所占的圆心角为82° D、如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人13. 已知 , , , ,若 ,且 ,则 的值可能是( )A、3 B、6 C、9 D、1214. 将图1中两个三角形按图2所示的方式摆放,其中四边形 为矩形,分别连接 、 .甲、乙两人有如下结论:甲:若四边形 为正方形,则四边形 必是正方形;
乙:若四边形 为正方形,则四边形 必是正方形.
下列判断正确的是( )
 A、甲正确,乙不正确 B、甲不正确,乙正确 C、甲、乙都不正确 D、甲、乙都正确
A、甲正确,乙不正确 B、甲不正确,乙正确 C、甲、乙都不正确 D、甲、乙都正确二、填空题
-
15. 在函数 中,自变量 的取值范围是 .16. 如图,则 的度数为 .
 17. 如图1,在 中, .动点 从 的顶点 出发,以 的速度沿 匀速运动回到点 .图2是点 运动过程中,线段 的长度 随时间 变化的图象.其中点 为曲线部分的最低点.
17. 如图1,在 中, .动点 从 的顶点 出发,以 的速度沿 匀速运动回到点 .图2是点 运动过程中,线段 的长度 随时间 变化的图象.其中点 为曲线部分的最低点.
 (1)、AB=;(2)、图2中,m= .
(1)、AB=;(2)、图2中,m= .三、解答题
-
18. 有一个容积为 的水池,现用10台抽水机从蓄满水的池中同时抽水,已知每台抽水机每小时可抽水 .(1)、抽水1小时后,池中还有水 ;(2)、在这一变化过程中哪些是变量,哪些是常量?19. 如图,点 表示学校的位置,点 表示游泳馆的位置,且点 在点 的正北方向距 点 处(每个单位表示 ).请你利用直角三角板(或量角器)以及所学知识解答下列问题:
 (1)、已知汽车站 在学校的北偏东30°方向距学校 处,请标出汽车站 的位置;(2)、若公园 与汽车站 关于直线 对称,请在图中标出公园的位置 ,并说明,对学校 而言,公园在它的什么位置.20. 将某雷达测速区监测到的一组汽车的时速数据整理,绘制成如下统计表和频数分布直方图.
(1)、已知汽车站 在学校的北偏东30°方向距学校 处,请标出汽车站 的位置;(2)、若公园 与汽车站 关于直线 对称,请在图中标出公园的位置 ,并说明,对学校 而言,公园在它的什么位置.20. 将某雷达测速区监测到的一组汽车的时速数据整理,绘制成如下统计表和频数分布直方图.统计表
时速
频数
频率
30
0.30
50
0.15
5
0.05
频数分布直方图

(注: 为时速大于或等于40千米而小于50千米,其他类同.)
(1)、请你把表中的数据填写完整;(2)、补全频数分布直方图;(3)、如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?21. 如图,已知四边形 为平行四边形, 、 分别平分 和 ,交 于点 、 ,连接 、 . (1)、若 ,求 的度数;(2)、求证:四边形 是平行四边形.22. 如图,已知直线 ,经过点 、点 ,交 轴于点 ,点 是 轴上一个动点,过点 、 作直线 .
(1)、若 ,求 的度数;(2)、求证:四边形 是平行四边形.22. 如图,已知直线 ,经过点 、点 ,交 轴于点 ,点 是 轴上一个动点,过点 、 作直线 .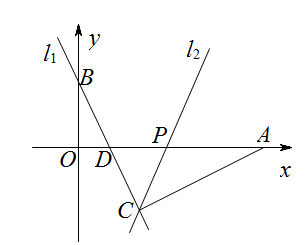 (1)、求直线 的表达式;(2)、已知点 ,当 时,求点 的坐标;(3)、设点 的横坐标为 ,点 , 是直线 上任意两个点,若 时,有 ,请直接写出 的取值范围.23. 已知,四边形 是菱形,延长 到 点,使 ,连接 、 相交于 点,连接 .
(1)、求直线 的表达式;(2)、已知点 ,当 时,求点 的坐标;(3)、设点 的横坐标为 ,点 , 是直线 上任意两个点,若 时,有 ,请直接写出 的取值范围.23. 已知,四边形 是菱形,延长 到 点,使 ,连接 、 相交于 点,连接 . (1)、求证: ;(2)、过 作 于 点.
(1)、求证: ;(2)、过 作 于 点.①已知 , ,求 的长;
②点 是对角线 上一点, ,若 是锐角三角形,求 的取值范围.
24. 某服装厂推出一款新式服装,出厂价定为200元/件,并为销售商提供了以下 、 两种优惠方案:方案 :一次性订购数量不低于40件的,每件按出厂价的 结算;
方案 :一次性订购金额超过5000元以上的部分,按出厂价的 结算;
甲销售商一次性订购了65件服装,按方案 结算;乙销售商按照方案 先后两次订购服装,第一次订购了30件,第二次订购了35件,两次共花了12700元.
设按照方案 、方案 订购 ( 为正整数)件服装的金额分别为 (元)、 (元)
(1)、求 与 的函数关系式;(2)、求 与 的函数关系式,并写出 的取值范围;(3)、服装厂根据销售情况,计划对方案 进行调整,结算百分比提高 个百分点( , 为整数),即将“ ”改为 ,使得一次性订购超过50件的,按照方案 更合算,请求出 的最小值.