安徽省马鞍山市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分）

1. 下列二次根式与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{18}$ C、 $\sqrt{12}$ D、 $\sqrt{9}$

查看试题解析
2. 下列几组数中，能作为直角三角形三边长度的是（）

A、6，9，10 B、5，12，17 C、4，5，6 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
3. 下列各式中，运算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、3 $\sqrt{2}$ - $\sqrt{2}$ =3 C、 $5 \times \sqrt{\frac{1}{5}} = 1$ D、 $\sqrt{12} \div \sqrt{3} = 2$

查看试题解析
4. 下列一元二次方程中，没有实数根的是（）

A、x²=2x B、2x²+3=0 C、x²+4x-1=0 D、x²-8x+16=0

查看试题解析
5. 已知一个菱形的边长是5cm，两条对角线长的比是4：3，则这个菱形的面积是（）

A、12cm² B、24cm² C、48cm² D、96cm²

查看试题解析
6. 一组数据3、4、x、1、4、3有唯一的众数3，则这组数据的方差是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如果一个多边形的内角和是外角和的3倍，那么这个多边形是

A、四边形 B、六边形 C、八边形 D、十边形

查看试题解析
8. 某单位为响应国家“厉行节约，反对浪费”的号召，减少了对办公经费的投入，在两个月内将开支从每月2500元降到1600元，若平均每月降低开支的百分率为x，则下列方程中正确的是（）

A、2500（1-x）²=1600 B、1600（1+x）²=2500 C、2500（1+x）²=1600 D、1600（1-x）²=2500

查看试题解析
9. 如图，在菱形ABCD中，∠B=45°，BC=2 $\sqrt{3}$ ，E、F分别是边CD、BC上的动点，连接AE和EF，G、H分别为AE、EF的中点，连接GH，则GH的最小值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{\sqrt{6}}{3}$ D、1

查看试题解析
10. 如图所示，E、F分别是正方形ABCD的边CD和AD上的点且CE=DF，AE、BF相交于点O，下列结论：①AE=BF；②AE⊥BF；③AO=OE；S_ΔAOB=S_{四边形DEOF}；⑤∠BAE=∠AFB，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（本大题共8小题，每小题3分，满分224分）

11. 若 $\sqrt{4 x + 1}$ 有意义，则x能取得的最小整数是_。

查看试题解析
12. 已知平行四边形ABCD的对角线AC、BD相交于点O，AC=24cm，BD=38cm，AD=14cm，则△OBC的周长为cm。

查看试题解析
13. 若数据2、3、5、3、8的众数是a，中位数是b，则a-b等于。

查看试题解析
14. 若m是方程x²+3x-2=0的一个根则3m²+9m+2021的值是。

查看试题解析
15. 如图，直线1上方有三个正方形a、b、c，若a、c的面积分别为1和9，则b的面积为；

查看试题解析
16. 如图，ΔABC的面积是16，点D、E、F、G分别是BC、AD、BE、CE的中点，则ΔAFG的面积是。

查看试题解析
17. 如图，将矩形ABCD沿对角线AC折叠，得到如图所示的图形，点B的对应点是B'，B'C与AD交于点E，若AB=2，BC=4，则AE的长是_。

查看试题解析
18. 如图，已知四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第2个正方形ACEF，再以第2个正方形的对角线AE为边作第3个正方形AEGH，如此下去，则第n个正方形的面积S_n= ．

查看试题解析

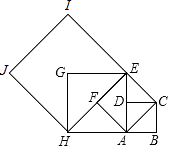
三、（本大题共6小题，满分46分）

19. 计算： ${(2 - \sqrt{3})}^{0} - \sqrt[3]{64} - {(\frac{1}{4})}^{- 1} + | \sqrt{3} - 2 |$

查看试题解析
20. 已知：关于x的方程x²+4x+2m=0有实根

(1)、求m的取值范围；

(2)、若m为正整数，且该方程的根都是整数，求m的值.

查看试题解析
21. 如图，在四边形ABCD中，AB//DC，AB=AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE。

(1)、求证：四边形ABCD是菱形；

(2)、若AB= $\sqrt{5}$ ，BD=2，求OE的长.

查看试题解析
22. 某校为加强学生的安全意识，每周通过安全教育平台向家长和学生推送安全教育宣传内容，并组织了一期防溺水安全知识竞赛，从参加竞赛的学生中抽取了部分学生成绩进行统计，绘制了图中两幅不完整的统计图。请回答如下问题：

(1)、m= ， α=；

(2)、补全频数直方图；

(3)、该校共有1600名学生，若认定成绩在60分及以下（含60分）的学生安全意识不强，有待进一步加强安全教育，请估计该校安全意识不强的学生约有多少人？

查看试题解析
23. 在丝绸博览会期间，某公司展销如图所示的长方形工艺晶，该工艺品长60cm ，宽40cm，中间镶有宽度相同的三条丝绸条带。

(1)、若丝绸条带的面积为650cm² ，求丝绸条带的宽度；

(2)、已知该工艺品的成本是40元/件，如果以单价为100元/件销售，那么每天可售出200件，另外每天除工艺品的成本外所需支付的各种费用是2000元，根据销售经验，如果将销售单价每降低1元，每天可多售出20件，请问该公司每天把销售单价定为多少元时，当日所获利润为22500元.

查看试题解析
24. 如图，矩形ABCD中，AD=2AB，E是AD边上一点，DE= $\frac{1}{n}$ AD（n为大于2的整数），连接BE，BE的垂直平分线分别交AD，BC于点F，G，FG与BE的交点为O，连接BF和EG。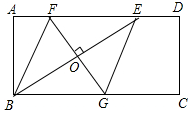

(1)、试判断四边形BFEG的形状，并说明理由；

(2)、当AB=4，n=3时，求FG的长；

(3)、记四边形BFEG的面积为S₁ ，矩形ABCD的面积为S₂ ，当 $\frac{S_{1}}{S_{2}} = \frac{17}{30}$ 时，求n的值（直接写出结果，不必写出解答过程）。

查看试题解析