山东省济南市历下区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-07-13 类型:期末考试
一、选择题(本大题共12个小题,每小题4分,共48分.)
-
1. 实数 , ,0,-2中,无理数是( )A、 B、 C、0 D、-22. 下面是华西、齐鲁、湘雅、协和四家医院的标志图案,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
3. 下列计算正确的是( )A、 B、 C、 D、4. 某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:支撑物的高度
10
20
30
40
50
60
70
80
小车下滑的时间
4.23
3.00
2.45
2.13
1.89
1.71
1.59
1.50
下列说法错误的是( )
A、当h=60cm时,t=1.71s B、随着h逐渐升高,t逐渐变小 C、h每增加10cm,t减小1.23s D、随着h逐渐升高,小车下滑的平均速度逐渐加快5. 如图,直角三角板 的直角顶点 在直线 上,若 , ,则 ( ) A、30° B、40° C、50° D、60°6. 下列说法正确的是( )A、“短跑运动员1秒跑完100米”是随机事件 B、“将油滴入水中,油会浮在水面”是不可能事件 C、“随意翻到一本书的某页,页码是奇数”是必然事件 D、“画一个三角形,其内角和一定等于180°”是必然事件7. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A、30° B、40° C、50° D、60°6. 下列说法正确的是( )A、“短跑运动员1秒跑完100米”是随机事件 B、“将油滴入水中,油会浮在水面”是不可能事件 C、“随意翻到一本书的某页,页码是奇数”是必然事件 D、“画一个三角形,其内角和一定等于180°”是必然事件7. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( ) A、① B、② C、③ D、④8. 以下列各组数为边长,不能构成直角三角形的是( )A、 , , B、1,1, C、6,8,10 D、 , ,9. 一个袋中装有红、黑、黄三种颜色小球共15个,这些球除颜色外均相同,其中红色球有5个,若从袋中任意取出一个球,取到黄色球的概率为 ,则黑色球个数为( )A、5 B、6 C、7 D、810. 若 在 的北偏西30°方向,那么 在 的( )方向.A、北偏西60° B、南偏东60° C、北偏西30° D、南偏东30°11. 如图所示,在 中, , , ,在 边上取一点 ,以 为折痕,使 的一部分与 重合, 与 延长线上的点 重合,则 的长为( )
A、① B、② C、③ D、④8. 以下列各组数为边长,不能构成直角三角形的是( )A、 , , B、1,1, C、6,8,10 D、 , ,9. 一个袋中装有红、黑、黄三种颜色小球共15个,这些球除颜色外均相同,其中红色球有5个,若从袋中任意取出一个球,取到黄色球的概率为 ,则黑色球个数为( )A、5 B、6 C、7 D、810. 若 在 的北偏西30°方向,那么 在 的( )方向.A、北偏西60° B、南偏东60° C、北偏西30° D、南偏东30°11. 如图所示,在 中, , , ,在 边上取一点 ,以 为折痕,使 的一部分与 重合, 与 延长线上的点 重合,则 的长为( ) A、7.5 B、8 C、8.5 D、912. 已知 表示取三个数中最小的那个数,例如:当 , .当 时,则 的值为( )A、 B、 C、 D、
A、7.5 B、8 C、8.5 D、912. 已知 表示取三个数中最小的那个数,例如:当 , .当 时,则 的值为( )A、 B、 C、 D、二、填空题(本大题共6个小题,每小题4分,共24分.)
-
13. 通过估算,比较大小:14. 计算: .15. 植树节过后,历下区园林绿化管理局为了考察树苗的成活率,于是进行了现场统计,表中记录了树苗的成活情况,则由此估计这种树苗成活的概率约为(结果精确到0.1)
植树总数
400
1500
3500
7000
9000
14000
成活数
369
1335
3203
6335
8073
12628
成活的频率
0.923
0.890
0.915
0.905
0.897
0.902
16. 如图, 是 的角平分线,点 是 上一点, 于点 ,点 是射线 上的一个动点,若 ,则 的最小值为. 17. 如图, , , .则正方形 的面积为.
17. 如图, , , .则正方形 的面积为.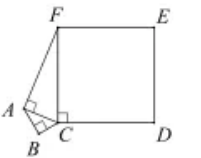 18. 如图,在 中, ,点 为线段 上一动点(不与点 , 重合),连接 ,作 , 交线段 于点 .下列结论:① ;② ;③当 为 中点时, ;④当 为等腰三角形时, .其中正确的是(填序号).
18. 如图,在 中, ,点 为线段 上一动点(不与点 , 重合),连接 ,作 , 交线段 于点 .下列结论:① ;② ;③当 为 中点时, ;④当 为等腰三角形时, .其中正确的是(填序号).
三、解答題(本大题共9个小题,共78分.)
-
19. 计算:(1)、 ;(2)、 .20. 在如图所示的正方形网格中,每个小正方形的边长为1,已知格点三角形 (顶点是网格线的交点的三角形).请用无刻度直尺按要求画图,保留作图痕迹.
 (1)、画出 关于直线 对称的 ;(2)、求 的面积;(3)、在直线 上找一点 ,使得 的值最小,最小值为.21. 已知某正数的两个平方根分别是 和 , 的立方根是2,求 的值.22. 如图,已知 , , .求证: 且 .
(1)、画出 关于直线 对称的 ;(2)、求 的面积;(3)、在直线 上找一点 ,使得 的值最小,最小值为.21. 已知某正数的两个平方根分别是 和 , 的立方根是2,求 的值.22. 如图,已知 , , .求证: 且 . 23. 如图1和图2均是一个均匀的可以自由转动的转盘,图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转);图2被涂上红色与绿色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色(当指针恰好指在分界线上时重转).小明转动图1的转盘,小亮转动图2的转盘.
23. 如图1和图2均是一个均匀的可以自由转动的转盘,图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转);图2被涂上红色与绿色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色(当指针恰好指在分界线上时重转).小明转动图1的转盘,小亮转动图2的转盘.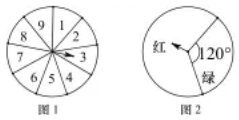 (1)、求小明转出的数字小于7的概率.(2)、小穎认为,小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同,她的看法对吗?为什么?24. 济南的泉城广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所.历下区某校七年级(1)班的小明和小亮同学学习了“勾股定理”之后,为了测得图中风筝的高度 ,他们进行了如下操作:
(1)、求小明转出的数字小于7的概率.(2)、小穎认为,小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同,她的看法对吗?为什么?24. 济南的泉城广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所.历下区某校七年级(1)班的小明和小亮同学学习了“勾股定理”之后,为了测得图中风筝的高度 ,他们进行了如下操作:
①测得 的长为15米(注: );
②根据手中剩余线的长度计算出风筝线 的长为25米;
③牵线放风筝的小明身高1.7米.
(1)、求风筝的高度 .(2)、过点 作 ,垂足为 ,求 的长度,25. 在 中, , 的垂直平分线交 于点 ,交 于点 , 的垂直平分线交 于点 ,交 于点 . (1)、如图1,若 , ,求 的度数;(2)、如图2,若 ,求证: ;(3)、当 是等腰三角形时,请直接写出所有可能的 与 的数量关系.26. 在防疫期间,某口罩生产厂为提高生产效益引进了新的设备,其中甲表示新设备的产量 (万个)与生产时间 (天)的关系,乙表示旧设备的产量 (万个)与生产时间 (天)的关系:
(1)、如图1,若 , ,求 的度数;(2)、如图2,若 ,求证: ;(3)、当 是等腰三角形时,请直接写出所有可能的 与 的数量关系.26. 在防疫期间,某口罩生产厂为提高生产效益引进了新的设备,其中甲表示新设备的产量 (万个)与生产时间 (天)的关系,乙表示旧设备的产量 (万个)与生产时间 (天)的关系: (1)、由图象可知,新设备因工人操作不当停止生产了天;在生产的第7天时,新设备比旧设备多生产万个口罩;(2)、请你求出新、旧设备每天分别生产多少万个口罩?(3)、在生产过程中,当 为何值时,新旧设备所生产的口罩数量相同,27. 本学期,我们学习了三角形相关知识,而四边形的学习,我们一般通过辅助线把四边形转化为三角形,通过三角形的基本性质和全等来解决一些问题.
(1)、由图象可知,新设备因工人操作不当停止生产了天;在生产的第7天时,新设备比旧设备多生产万个口罩;(2)、请你求出新、旧设备每天分别生产多少万个口罩?(3)、在生产过程中,当 为何值时,新旧设备所生产的口罩数量相同,27. 本学期,我们学习了三角形相关知识,而四边形的学习,我们一般通过辅助线把四边形转化为三角形,通过三角形的基本性质和全等来解决一些问题. (1)、如图1,在四边形 中, , ,连接 .
(1)、如图1,在四边形 中, , ,连接 .①小明发现,此时 平分 .他通过观察、实验,提出以下想法:延长 到点 ,使得 ,连接 ,证明 ,从而利用全等和等腰三角形的性质可以证明 平分 .请你参考小明的想法,写出完整的证明过程.
②如图2,当 时,请你判断线段 , , 之间的数量关系,并证明.
(2)、如图3,等腰 、等腰 的顶点分别为 、 ,点 在线段 上,且 ,请你判断 与 的数量关系,并证明.四、附加题(本大题共3个题,满分共20分,得分单独评价.)
-
28. 如图, , , ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,设运动时间为 ,则当 与 全等时,点 的运动速度为( )
 A、 B、 C、 D、29. 先阅读下面的解题过程,然后再解答:
A、 B、 C、 D、29. 先阅读下面的解题过程,然后再解答:形如 的化简,只要我们找到两个数 , ,使 , ,即 , ,则有: .
(1)、根据上述方法化简:① ;
② .
(2)、已知 ,则 .30. 定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”.例如:等腰直角三角形就是“半角三角形”.在钝角三角形 中, , , ,过点 的直线 交 边于点 .点 在直线 上,且 . (1)、如图1,若 , ,点 在 延长线上,图中是否存在“半角三角形”( 除外),若存在,请写出图中的“半角三角形",并证明;若不存在,请说明理由;(2)、如图2,若 ,保持 的度数与(1)中的结论相同,请直接写出 , , 满足的数量关系.
(1)、如图1,若 , ,点 在 延长线上,图中是否存在“半角三角形”( 除外),若存在,请写出图中的“半角三角形",并证明;若不存在,请说明理由;(2)、如图2,若 ,保持 的度数与(1)中的结论相同,请直接写出 , , 满足的数量关系.