云南省腾冲市2021年中考数学模拟试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、填空题
-
1. 计算:-3+2= .2. 分解因式: =.3. 若 , ,则 .4. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .5. 小明同学10个周的综合素质评价成绩如下:
成绩(分)
94
95
97
98
100
周数(个)
1
2
2
3
2
这10个周的综合素质评价成绩的中位数和众数分别是 .
6. 如图,在矩形 中, , ,点 在边 上,且 .连接 ,将 沿 折叠,若点 的对应点 落在矩形 的边上,则 的值为 .
二、单选题
-
7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,四边形 内接于⊙O,若 ,则 的度数为( )
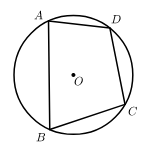 A、18 B、72 C、100 D、1089. 全国脱贫攻坚总结表彰大会于2021年2月25日上午在北京人民大会堂隆重举行.中共中央总书记、国家主席、中央军委主席习近平强调,经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽,12.8万个贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹!这是中国人民的伟大光荣,是中国共产党的伟大光荣,是中华民族的伟大光荣.数据9899万用科学记数法表示为( )A、 B、 C、 D、10. 如图,若 , ,若 ,则 的度数为( )
A、18 B、72 C、100 D、1089. 全国脱贫攻坚总结表彰大会于2021年2月25日上午在北京人民大会堂隆重举行.中共中央总书记、国家主席、中央军委主席习近平强调,经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽,12.8万个贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹!这是中国人民的伟大光荣,是中国共产党的伟大光荣,是中华民族的伟大光荣.数据9899万用科学记数法表示为( )A、 B、 C、 D、10. 如图,若 , ,若 ,则 的度数为( )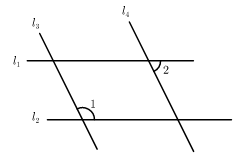 A、 B、 C、 D、11. 如图,点 , , 在正方形网格的格点上,则 等于( )
A、 B、 C、 D、11. 如图,点 , , 在正方形网格的格点上,则 等于( ) A、 B、 C、 D、12. 函数 的自变量 的取值范围是( )A、 B、 C、 D、 取任意实数13. 如图是一个几何体的三视图,则这个几何体的侧面积是( )
A、 B、 C、 D、12. 函数 的自变量 的取值范围是( )A、 B、 C、 D、 取任意实数13. 如图是一个几何体的三视图,则这个几何体的侧面积是( ) A、 B、 C、 D、14. 已知二次函数 的图象经过 与 两点,关于 的方程 有两个根,其中一个根是5.则关于 的方程 有两个整数根,这两个整数根是( )A、-2或4 B、-2或0 C、0或4 D、-2或5
A、 B、 C、 D、14. 已知二次函数 的图象经过 与 两点,关于 的方程 有两个根,其中一个根是5.则关于 的方程 有两个整数根,这两个整数根是( )A、-2或4 B、-2或0 C、0或4 D、-2或5三、解答题
-
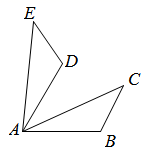
15. 解不等式组: .16. 如图, , , .求证: .
 17. 先化简,再求值: ,其中 是9的算术平方根.18. 如图,在菱形 中,对角线 , 交于点 ,过点 , ,分别作 , ,垂足分别为 , .
17. 先化简,再求值: ,其中 是9的算术平方根.18. 如图,在菱形 中,对角线 , 交于点 ,过点 , ,分别作 , ,垂足分别为 , . (1)、求证:四边形 是矩形.(2)、若 ,S菱形ABCD ,求 的长.19. 为了了解某校九年级全体女生800米跑步的成绩,随机抽取了部分女生进行测试,并将测试成绩分为 , , , 四个等级,绘制如下不完整的统计图表,如图表所示,根据图表信息解答下列问题:
(1)、求证:四边形 是矩形.(2)、若 ,S菱形ABCD ,求 的长.19. 为了了解某校九年级全体女生800米跑步的成绩,随机抽取了部分女生进行测试,并将测试成绩分为 , , , 四个等级,绘制如下不完整的统计图表,如图表所示,根据图表信息解答下列问题:成绩等级频数分布表
成绩等级
频数
24
14
2
合计
 (1)、 , , 扇形图中B的圆心角的度数为度;(2)、甲、乙、丙、丁是A等级中的四名学生,学校决定从这四名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽取乙、丙两名学生的概率.20. 如图,在 中, , ,点 在边 上, 经过点 和点 且与边 相交于点 .
(1)、 , , 扇形图中B的圆心角的度数为度;(2)、甲、乙、丙、丁是A等级中的四名学生,学校决定从这四名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽取乙、丙两名学生的概率.20. 如图,在 中, , ,点 在边 上, 经过点 和点 且与边 相交于点 .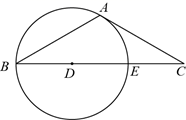 (1)、判断 与⊙D的位置关系,并说明理由;(2)、若 ,求⊙D的半径.21. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)、判断 与⊙D的位置关系,并说明理由;(2)、若 ,求⊙D的半径.21. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是1. (1)、求反比例函数的表达式.(2)、将一次函数 的图象向下平移4个单位长度,求平移后的图象与反比例函数 图象的交点坐标.22. 公司小李驾驶一辆小车到 市出差,将车停在了 市一个停车场里,该停车场收费标准如下表:
(1)、求反比例函数的表达式.(2)、将一次函数 的图象向下平移4个单位长度,求平移后的图象与反比例函数 图象的交点坐标.22. 公司小李驾驶一辆小车到 市出差,将车停在了 市一个停车场里,该停车场收费标准如下表:时段
收费标准
备注
白天停车
07时—22时(小车)
停车3小时以内(含3小时)5元/辆·次,超过3小时,每小时加收3元.
持续几天停车,仅前3小时收费5元;超过3小时,不足1小时的按1小时计算收费.
07时—22时(大车)
停车3小时以内(含3小时)10元/辆·次,超过3小时,每小时加收5元.
夜间停车
22时—07时(小车)
无论停车时间长短10元/辆·次
22时—07时(大车)
无论停车时间长短20元/辆·次
(1)、设小李白天停车时长为 小时,应交停车总费用为 元,请写出 与 的函数表达式;(2)、如果小李是4月23日上午10:05 时驾车进入停车(开始计时收费),至次日中午12:30时驾驶车辆驶出停车场(收费计时结束),小李应交停车费多少元?23. 如图,抛物线 经过点 和点 ,与 交于点 ,顶点为 ,连接 、 , 与抛物线的对称轴 交于点 .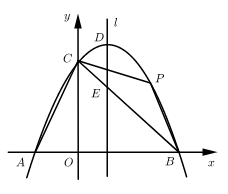 (1)、求该抛物线的函数表达式;(2)、点 是第一象限抛物线上的动点,连接 , ,当四边形 面积取最大值时,求点 的坐标;(3)、点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以 , , 为顶点的三角形与 相似?若存在,求点 的坐标;若不存在,请说明理由.
(1)、求该抛物线的函数表达式;(2)、点 是第一象限抛物线上的动点,连接 , ,当四边形 面积取最大值时,求点 的坐标;(3)、点 是对称轴 右侧抛物线上的动点,在射线 上是否存在点 ,使得以 , , 为顶点的三角形与 相似?若存在,求点 的坐标;若不存在,请说明理由.