辽宁省营口市2021年中考数学二模试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、单选题
-
1. 在下列各数中,比 大的数是( )A、 B、 C、0 D、2. 如图所示的几何体的从左面看到的图形为( )
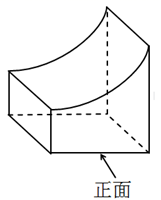 A、
A、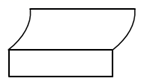 B、
B、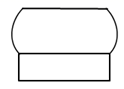 C、
C、 D、
D、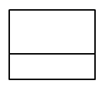 3. 下列运算正确的是( )A、 B、 C、 D、4. 2021年5月11日,第七次全国人口普查数据公布,我国总人口达到14.1亿人,的占全球总人口的18%,仍然是世界上第一人口大国,其中14.1亿用科学记数法表示为( )A、 B、 C、 D、5. 一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):
3. 下列运算正确的是( )A、 B、 C、 D、4. 2021年5月11日,第七次全国人口普查数据公布,我国总人口达到14.1亿人,的占全球总人口的18%,仍然是世界上第一人口大国,其中14.1亿用科学记数法表示为( )A、 B、 C、 D、5. 一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
则被遮盖的两个数据依次是( )
A、 B、 C、 D、6. 如图,点A在反比例函数y= (x<0)的图象上,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交x轴于点B,当AC=1时,△ABC的周长为( ) A、1 B、 C、 +1 D、 +27.
A、1 B、 C、 +1 D、 +27.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
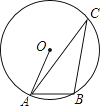 A、55° B、60° C、65° D、70°8. 如图, 在平面直角坐标系中, 的顶点 与原点重合,点 在 轴的正半轴上, 按以下步骤作图:①以点 为圆心,适当长度为半径作 弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧, 两弧在 内交于点 ;③作射线 ,交边 于点 .若 , ,则点 的坐标为( )
A、55° B、60° C、65° D、70°8. 如图, 在平面直角坐标系中, 的顶点 与原点重合,点 在 轴的正半轴上, 按以下步骤作图:①以点 为圆心,适当长度为半径作 弧,分别交边 , 于点 , ;②分别以点 , 为圆心,大于 的长为半径作弧, 两弧在 内交于点 ;③作射线 ,交边 于点 .若 , ,则点 的坐标为( ) A、 B、 C、 D、9. 如图,已知点 、 分别在 的边 、 上, ,点 在 延长线上, ,则下列结论错误的是( )
A、 B、 C、 D、9. 如图,已知点 、 分别在 的边 、 上, ,点 在 延长线上, ,则下列结论错误的是( ) A、 B、 C、 D、10. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( )
A、 B、 C、 D、10. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( ) A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题
-
11. 函数 中,自变量 的取值范围是 .12. 把 分解因式的结果是.13. 游客到某景区旅游,经过景区检票口时,共有3个检票通道A、B、C,游客可随机选择其中一个通过,两名游客经过次检票口时,则他们选择不同通道通过的概率是 .14. 如图, 中 , ,将 绕点A按顺时针方向旋转 得到 ,连接 ,则 的长为 .
 15. 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作 .过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
15. 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作 .过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 . 16. 如图,已知 是 轴上的点,且 ,分别过点 作 轴的垂线交一次函数 的图象于点 ,连接 依次产生交点 ,则 的横坐标是 .
16. 如图,已知 是 轴上的点,且 ,分别过点 作 轴的垂线交一次函数 的图象于点 ,连接 依次产生交点 ,则 的横坐标是 .
三、解答题
-
17. 先化简,再求值: ,然后从 的范围内选取一个合适的整数作为 的值代入求值.18. 为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有3个不同的操作实验题目,物理题目用序号①、②、③、④表示,化学题目用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.(1)、小李同学抽到物理实验题目①这是一个事件(填“必然”、“不可能”或“随机”).(2)、小张同学对物理的①、②和化学的a、c号实验准备得较好,请用画树形图(或列表)的方法,求他同时抽到两科都准备得较好的实验题目的概率.19. 了解学生每天的睡眠情况,某初中学校从全校800名学生中随机抽取了40名学生,调查了他们平均每天的睡眠时间(单位,h)9,8,10.5,7,9,8,10,8,9,9.5,7.5,9,8.5,7.5,9.5,8,9,7,9.5,9,7,9,9,7.5,8.5,9,8,7.5,9.5,9.5,8.5,9,8,9.5,8,9,9,10,8.5,10.5;在对这些数据整理后,绘制了如图的统计图表:
睡眠时间分组统计表
组别
睡眠时间分组
人数(频数)
1
2
11
3
4
4

请根据以上信息,解答下列问题:
(1)、 , , , ;(2)、抽取的这40名学生平均每天睡眼时间的中位数落在组(填组别),在扇形统计图中第4组所在扇形的圆心角是度;(3)、如果按照学校要求,学生平均每天的睡眠时间应不少于 .请估计该校学生中睡眠时间符合要求的人数.20. 某书店在图书批发中心选购 两种科普书, 种科普书每本进价比 种科普书每本进价多 元.若用 元购进 种科普书的数量是用 元购进 种科普书数量的 倍.(1)、求 两种科普书每本进价各是多少元;(2)、该书店计划 种科普书每本售价为 元, 种科普书每本售价为 元,购进 种科普书的数量比购进 种科普书的数量的 还少 本,若 两种科普书全部售出,使总获利超过 元,则至少购进 种科普书多少本?21. 如图,要测量一垂直于水平面的建筑物AB的高度,小明从建筑物底端B出发,沿水平方向向右走30米到达点C,又经过一段坡角为30°,长为20米的斜坡CD,然后再沿水平方向向右走了50米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,求建筑物AB的高度.(结果保留根号,参考数据:sin24°≈ ,cos24°≈ ,tan24°= ) 22. 如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E.
22. 如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E. (1)、判断DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为5, ,求CE的长.23. 某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD所示(不包括端点A).
(1)、判断DE与⊙O的位置关系,并说明理由;(2)、若⊙O的半径为5, ,求CE的长.23. 某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD所示(不包括端点A).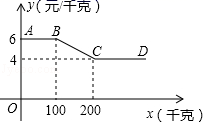 (1)、当100<x<200时,直接写y与x之间的函数关系式: .(2)、蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?(3)、在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?24. 如图, 中, ,过点A作射线 ,点D是线段 上一动点(不与点 重合),连接 ,过点D作 ,交射线 于点E.
(1)、当100<x<200时,直接写y与x之间的函数关系式: .(2)、蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?(3)、在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?24. 如图, 中, ,过点A作射线 ,点D是线段 上一动点(不与点 重合),连接 ,过点D作 ,交射线 于点E. (1)、如图①,当 时,猜想线段 与线段 的数量关系,并说明理由;(2)、如图②,当 时,猜想线段 与线段 的数量关系,并说明理由;(3)、当 时,直接写出线段 与线段 的数量关系(用含 的式子表示)25. 如图,在平面直角坐标系中,二次函数 ( )的图象经过点 和点 ,与 轴交于点 ,连接 , ,现有两动点 , 分别从 , 两点同时出发,点 以每秒4个单位的速度沿 向终点 移动,点 以每秒1个单位的速度沿 向点 移动点 停止运动时,点 也同时停止运动,线段 , 相交于点 ,过点 作 ,交 于点 ,射线 交 轴于点 ,设动点 、 移动的时间为 (单位:秒).
(1)、如图①,当 时,猜想线段 与线段 的数量关系,并说明理由;(2)、如图②,当 时,猜想线段 与线段 的数量关系,并说明理由;(3)、当 时,直接写出线段 与线段 的数量关系(用含 的式子表示)25. 如图,在平面直角坐标系中,二次函数 ( )的图象经过点 和点 ,与 轴交于点 ,连接 , ,现有两动点 , 分别从 , 两点同时出发,点 以每秒4个单位的速度沿 向终点 移动,点 以每秒1个单位的速度沿 向点 移动点 停止运动时,点 也同时停止运动,线段 , 相交于点 ,过点 作 ,交 于点 ,射线 交 轴于点 ,设动点 、 移动的时间为 (单位:秒). (1)、求经过 , , 三点的二次函数解析式;(2)、点 、点 在运动过程中, 的面积是否总为定值?若是,求出此定值;若不是,请说明理由.(3)、当 为何值时, 为等腰三角形?请写出解答过程.
(1)、求经过 , , 三点的二次函数解析式;(2)、点 、点 在运动过程中, 的面积是否总为定值?若是,求出此定值;若不是,请说明理由.(3)、当 为何值时, 为等腰三角形?请写出解答过程.