江西省九江市2021年中考数学二模试卷

试卷更新日期：2021-07-13 类型：中考模拟

进入出卷网下载

一、单选题

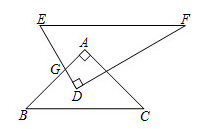
1. 已知某新型感冒病毒的直径约为0.000000823米，将0.000000823用科学记数法表示为（）

A、8.23×10^﹣⁶ B、8.23×10^﹣⁷ C、8.23×10⁶ D、8.23×10⁷

查看试题解析
2. -2021的绝对值等于（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
3. 下列等式成立的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(- x^{3})}^{2} = x^{6}$ C、 $(- a^{3}) \cdot a^{3} = a^{6}$ D、 $4 a^{2} - {(2 a)}^{2} = 2 a^{2}$

查看试题解析
4. 如图摆放的一副学生用直角三角板， $∠ F = 30^{\circ} ， ∠ C = 45^{\circ}$ ， $A B$ 与 $D E$ 相交于点G，当 $E F // B C$ 时， $∠ E G B$ 的度数是（）

A、135° B、120° C、115° D、105°

查看试题解析
5. 已知一元二次方程 $x^{2} - 4 x + 3 = 0$ 的两根 $x_{1}$ 、 $x_{2}$ ，则 $x_{1} + x_{2} =$ （）

A、4 B、3 C、-4 D、-3

查看试题解析
6. 如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形（简称格点正方形）.若再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠，且组成的图形既是轴对称图形，又是中心对称图形，则这个格点正方形的作法共有（）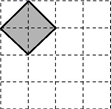

A、2种 B、3种 C、4种 D、5种

查看试题解析

二、填空题

7. 若 $\sqrt{2 x - 6}$ 有意义，则 $x$ 的取值范围是

查看试题解析
8. 公元3世纪，我过古代数学家就能利用近似公式 $\sqrt{a^{2} + r} = a + \frac{r}{2 a}$ 得到无理数的近似值，例如： $\sqrt{2}$ 化为 $\sqrt{1^{2} + 1}$ ，再由近似公式得到 $\sqrt{2} \approx 1 + \frac{1}{2 \times 1} = \frac{3}{2} = 1.5$ ，若利用此公式计算 $\sqrt{17}$ 的近似值时， $r$ 取正整数，且 $a$ 取尽可能大的正整数，则 $\sqrt{17} \approx$ ．

查看试题解析
9. 如图设计一张折叠型方桌子，若 $A O = B O = 50 cm$ ， $C O = D O = 30 cm$ ，将桌子放平后，要使AB距离地面的高为40cm，则两条桌腿需要叉开的 $∠ A O B$ 应为．

查看试题解析
10. 一个几何体的三视图如图所示，其中主视图和俯视图都是矩形，则它的表面积是.

查看试题解析
11. 一个样本为1，3，2，2，a，b，c，已知这个样本的众数为3，平均数为2，则这组数据的中位数为．

查看试题解析
12. 如图，在正方形ABCD中，E是BC边上一点，连接AE， $A B = 4 C E$ ，F是AE上一点，射线BF与正方形的边交于点G（不同于点B），若 $B G = A E$ ，则 $\frac{B F}{B G} =$ ．

查看试题解析

三、解答题

13. 解方程： $\frac{x}{x - 1} + 1 = \frac{2}{x - 1}$ .

查看试题解析
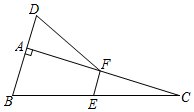
14. 如图，已知：在 $Δ A B C$ 中， $∠ B A C = 90^{°}$ ，延长BA到点D ，使 $A D = \frac{1}{2} A B$ ，点E ， F分别是边BC ， AC的中点．求证： $D F = B E$ ．

查看试题解析
15. 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为 $\frac{1}{2}$ 。

(1)、布袋里红球有多少个？

(2)、先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率。

查看试题解析
16. 如图，四边形ABCD是平行四边形，点A，B，D均在圆上．请仅用无刻度的直尺分别下列要求画图．

(1)、在图①中，若AB是直径，CD与圆相切，画出圆心 $O$ ；

(2)、在图②中，若CB，CD均与圆相切，画出圆心 $O$ ．

查看试题解析
17. 在平面直角坐标系中，一次函数y=kx+b（k，b都是常数，且k≠0）的图象经过点（1，0）和（0，2）．

(1)、当﹣2＜x≤3时，求y的取值范围；

(2)、已知点P（m，n）在该函数的图象上，且m﹣n=4，求点P的坐标．

查看试题解析
18. 某校随机抽取部分学生，就“学习习惯”进行调查，将“对自己做错的题目进行整理、分析、改正”（选项为：很少、有时、常常、总是）的调查数据进行了整理，绘制成部分统计图如下：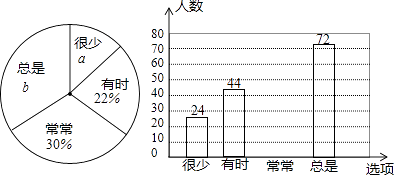
请根据图中信息，解答下列问题

(1)、该调查的样本容量为， a=%，b=%，“常常”对应扇形的圆心角为°

(2)、请你补全条形统计图；

(3)、若该校共有3200名学生，请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名？

查看试题解析
19. 如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块E，H可分别沿等长的立柱AB，DC上下移动，AF＝EF＝FG＝1m．

(1)、若移动滑块使AE＝EF，求∠AFE的度数和棚宽BC的长．

(2)、当∠AFE由60°变为74°时，问棚宽BC是增加还是减少？增加或减少了多少？（结果精确到0.1m．参考数据： $\sqrt{3}$ ≈1.73，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
20. 如图：直线y=x与反比例函数y= $\frac{k}{x}$ （k＞0）的图象在第一象限内交于点A（2，m）．

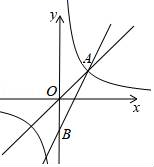(1)、求m、k的值；

(2)、点B在y轴负半轴上，若△AOB的面积为2，求AB所在直线的函数表达式；

(3)、将△AOB沿直线AB向上平移，平移后A、O、B的对应点分别为A'、O'、B'，当点O'恰好落在反比例函数y= $\frac{k}{x}$ 的图象上时，求点A'的坐标．

查看试题解析
21. 如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF=∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG，．

(1)、求证：DF是⊙O的切线；

(2)、若AD=DP，OB=3，求 $\overset{⌢}{B D}$ 的长度；

(3)、若DE=4，AE=8，求线段EG的长．

查看试题解析
22. 已知抛物线 $C_{1} ： y = {ax}^{2} + 4 ax + 4 a + b (a \neq 0 ， b > 0)$ 的顶点为 $M$ ，经过原点 $O$ 且与 $x$ 轴另一交点为 $A$ ．

(1)、求点 $A$ 的坐标；

(2)、若 $△ AMO$ 为等腰直角三角形，求抛物线 $C_{1}$ 的解析式；

(3)、现将抛物线 $C_{1}$ 绕着点 $P (m ， 0)$ 旋转 $180^{\circ}$ 后得到抛物线 $C_{2}$ ，若抛物线 $C_{2}$ 的顶点为 $N$ ，当 $b = 1$ ，且顶点 $N$ 在抛物线 $C_{1}$ 上时，求 $m$ 的值．

查看试题解析
23. 定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形，根据以上定义，解决下列问题：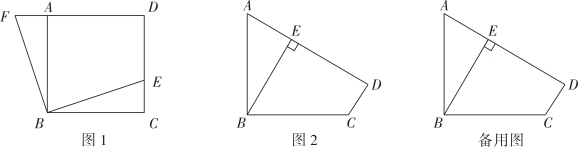

(1)、如图1，正方形 $A B C D$ 中，E是 $C D$ 上的点，将 $Δ B C E$ 绕B点旋转，使 $B C$ 与 $B A$ 重合，此时点E的对应点F在 $D A$ 的延长线上，则四边形 $B E D F$ 为“直等补”四边形，为什么？

(2)、如图2，已知四边形 $A B C D$ 是“直等补”四边形， $A B = B C = 5$ ， $C D = 1$ ， $A D > A B$ ，点 $B$ 到直线 $A D$ 的距离为 $B E$ ．
①求 $B E$ 的长．

②若M、N分别是 $A B$ 、 $A D$ 边上的动点，求 $Δ M N C$ 周长的最小值．

查看试题解析