吉林省长春市南关区2021年中考数学一模试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、单选题
-
1. 在实数0.3, , , 中,最小的是( )A、0.3 B、 C、 D、2. 2021年2月,中共中央、国务院印发了《国家综合立体交通网规划纲要》,到2035年,国家综合立体交通网实际线网总规模合计70万公里左右,70万公里即700 000公里.700 000这个数用科学记数法表示为( )A、7×104 B、7 105 C、0.7 106 D、7 1063. 下图是由4个相同的小长方体组成的立体图形和它的主视图,则它的左视图为( )
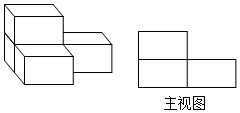 A、
A、 B、
B、 C、
C、 D、
D、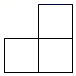 4. 下列运算一定正确的是( )A、 B、 C、 D、5. 如图,在 岛周围20海里水域有暗礁,一艘轮船由西向东航行到 处时,发现岛在北偏东64°的方向且与轮船相距52海里.若该轮船不改变航向,为航行安全,需要计算 到 的距离 .下列算法正确的是( )
4. 下列运算一定正确的是( )A、 B、 C、 D、5. 如图,在 岛周围20海里水域有暗礁,一艘轮船由西向东航行到 处时,发现岛在北偏东64°的方向且与轮船相距52海里.若该轮船不改变航向,为航行安全,需要计算 到 的距离 .下列算法正确的是( ) A、 B、 C、 D、6. 如图,在 中, 按以下步骤作图:分别以点 和 为圆心,大于 的边长为半径作圆弧,两弧相交于点 和 ;作直线 交 于点 ,连结 .若 ,则 的长可能是( )
A、 B、 C、 D、6. 如图,在 中, 按以下步骤作图:分别以点 和 为圆心,大于 的边长为半径作圆弧,两弧相交于点 和 ;作直线 交 于点 ,连结 .若 ,则 的长可能是( )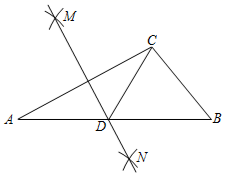 A、 B、 C、 D、7. 如图, 的弦 、 的延长线交圆外于点 ,若 , ,则 的大小是( )
A、 B、 C、 D、7. 如图, 的弦 、 的延长线交圆外于点 ,若 , ,则 的大小是( )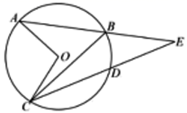 A、20° B、25° C、30° D、50°8. 如图,在平面直角坐标系中,抛物线 ( )交 轴正半轴于点 ,交 轴于点 ,线段 轴交此抛物线于点 ,且 ,则 的面积是( )
A、20° B、25° C、30° D、50°8. 如图,在平面直角坐标系中,抛物线 ( )交 轴正半轴于点 ,交 轴于点 ,线段 轴交此抛物线于点 ,且 ,则 的面积是( ) A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3二、填空题
-
9. 计算 =10. 不等式3x-12>0的解集是 .11. 如图,D是△ABC的AC边上一点,且AD=DB,CD=CB.若∠C=100°,则∠A= .
 12. 如图, 是边长为6的等边三角形,分别以点 、 、 为圆心,以2为半径画弧,则图中阴影部分图形的周长为 . (结果保留 )
12. 如图, 是边长为6的等边三角形,分别以点 、 、 为圆心,以2为半径画弧,则图中阴影部分图形的周长为 . (结果保留 )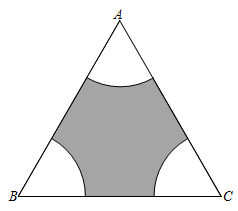 13. 如图,将△ABC沿其中位线DE翻折,点A落在BC边上的A′处.若BA′:A′C=2:1,且△DB A′的面积为4,则△ABC的面积为 .
13. 如图,将△ABC沿其中位线DE翻折,点A落在BC边上的A′处.若BA′:A′C=2:1,且△DB A′的面积为4,则△ABC的面积为 . 14. 如图,在平面直角坐标系中,AB= ,点A在y轴正半轴上,点B的坐标为(-1,-1).把线段AB沿垂直于AB的方向平移,当点A的对应点A′在函数 的图象上时,点B的对应点B′恰好在x轴负半轴上,则k的值为 .
14. 如图,在平面直角坐标系中,AB= ,点A在y轴正半轴上,点B的坐标为(-1,-1).把线段AB沿垂直于AB的方向平移,当点A的对应点A′在函数 的图象上时,点B的对应点B′恰好在x轴负半轴上,则k的值为 .
三、解答题
-
15. 先化简,再求值: ,其中 .16. 今年是农历辛丑年,即牛年.如图,现有三张正面印有不同牛图案的不透明卡片 、 、 ,卡片除正面图案不同外其余均相同,将三张卡片正面向下洗匀小宇从中随机抽取两张卡片请用画树形图或列表的方法,求小宇抽出的两张卡片中必有一张 卡片的概率.
 17. 图①、图②均是 的正方形网格,每个小正方形的顶点称为格点,点 、 、 均在格点上在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法,要求保留必要的作图痕迹.
17. 图①、图②均是 的正方形网格,每个小正方形的顶点称为格点,点 、 、 均在格点上在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法,要求保留必要的作图痕迹. (1)、在图①中画一个以 为一腰的等腰三角形 .(2)、在图②中过点 画 的垂线 .18. 2020年11月19日,长春发生了罕见的冻雨灾害,市政清洁队一个小分队承担着2100米长的道路冰雪清理任务.为了提高清理进度,在清理了300米后增加了人数和设备,清理效率是原来的4倍,结果共用了5小时就完成了清理任务求原来每小时清理的长度.19. 如图,在△ABC中,∠C=90°,点O为AB上一点,以OA为半径的⊙O与BC相切于点D,连结AD,过D作DE⊥AB,垂足为点E.
(1)、在图①中画一个以 为一腰的等腰三角形 .(2)、在图②中过点 画 的垂线 .18. 2020年11月19日,长春发生了罕见的冻雨灾害,市政清洁队一个小分队承担着2100米长的道路冰雪清理任务.为了提高清理进度,在清理了300米后增加了人数和设备,清理效率是原来的4倍,结果共用了5小时就完成了清理任务求原来每小时清理的长度.19. 如图,在△ABC中,∠C=90°,点O为AB上一点,以OA为半径的⊙O与BC相切于点D,连结AD,过D作DE⊥AB,垂足为点E. (1)、求证:AD平分∠CAB.(2)、若AB=20,且AE:EB=3:2,则⊙O的半径为 .20. 校学生处为了解全校1200名学生每天在上学路上所用的时间,随机调查了30名学生.下表是某一天这30名学生上学所用时间(单位:分):
(1)、求证:AD平分∠CAB.(2)、若AB=20,且AE:EB=3:2,则⊙O的半径为 .20. 校学生处为了解全校1200名学生每天在上学路上所用的时间,随机调查了30名学生.下表是某一天这30名学生上学所用时间(单位:分):20
20
30
15
20
25
5
15
20
10
15
35
45
10
20
25
30
20
15
20
20
10
20
5
15
20
20
20
5
15
通过整理和分析数据,得到以下不完全的统计图表.

样本数据平均数、中位数、众数、方差一览表:
平均数
中位数
众数
方差
18.8
72.8
根据以上信息,解答下列问题.
(1)、补全条形统计图.(2)、 ; .(3)、若随机问这30名同学一名学生的上学时间,最有可能得到的回答是多少分钟?(4)、估计全校学生上学时间在20分钟及以下的人数.21. 从地面到高空,气温随离地面高度的变化而变化,当到达一定高度后,气温几乎不再变化.如图是气温 (℃)与离地面高度 ( )之间函数的图象.根据图象解答下列问题: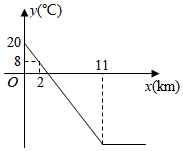 (1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.22. 下面是华师版八年级下册数学教材第121页的第1题,请结合图①完成这道题的证明.(1)、如图①,点E是正方形ABCD的边CD上的一点,点F是CB的延长线上的一点,且EA⊥AF.求证:DE=BF.
(1)、求地面的气温.(2)、当 时,求 与 之间的函数关系式.(3)、若离地面不同高度的两处气温差为3℃,直接写出这两处中较低处离地面高度 ( )的取值范围.22. 下面是华师版八年级下册数学教材第121页的第1题,请结合图①完成这道题的证明.(1)、如图①,点E是正方形ABCD的边CD上的一点,点F是CB的延长线上的一点,且EA⊥AF.求证:DE=BF. (2)、如图②,在△ABC中,∠ACB=90°,AC=CB= ,CD⊥AB,垂足为点D,点E是边AC上的动点,点F是边CB上的一点,且ED⊥DF.
(2)、如图②,在△ABC中,∠ACB=90°,AC=CB= ,CD⊥AB,垂足为点D,点E是边AC上的动点,点F是边CB上的一点,且ED⊥DF.①直接写出四边形EDFC的面积.
②若∠CDE=15°,则四边形EDFC的周长为 ▲ .
23. 如图,在△ABC中,AB=AC,BD⊥AC于点D,AB= ,BD= .动点P从点A出发,沿AB—BC向终点C运动,点P在AB上的运动速度是每秒 个单位长度,在BC上的运动速度是每秒5个单位长度.当点P不与△ABC顶点重合时,以PB为角的一边作∠BPQ=∠A,角的另一边交BC边或AB边于点Q,以PQ为一边在PQ的下方作正方形PQMN.设点P的运动时间为t秒,正方形PQMN与△ABC重合部分图形的面积为S.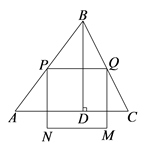 (1)、求∠C的正切值.(2)、用t的代数式表示PB的长.(3)、当点P在AB上运动时,求S的最大值以及S取得最大值时t的值.(4)、当正方形PQMN的顶点在边AC上时,直接写出t的值.24. 在平面直角坐标系中,把函数 ( 、 为常数)的图象记为 .(1)、求 与 轴交点的坐标.(2)、当 时, 与 只有一个交点,求 的值.(3)、①设 ,若点 在 上,则点 必在 上,且 过点 ,求 的函数表达式.
(1)、求∠C的正切值.(2)、用t的代数式表示PB的长.(3)、当点P在AB上运动时,求S的最大值以及S取得最大值时t的值.(4)、当正方形PQMN的顶点在边AC上时,直接写出t的值.24. 在平面直角坐标系中,把函数 ( 、 为常数)的图象记为 .(1)、求 与 轴交点的坐标.(2)、当 时, 与 只有一个交点,求 的值.(3)、①设 ,若点 在 上,则点 必在 上,且 过点 ,求 的函数表达式.②点 、 是①中函数图象上的两点,比较 与 的大小.
③点 、 是①中函数图象上的两点,比较 与 的大小.
(4)、矩形 四个顶点的坐标分别为 、 、 、 ,当 时,函数 ( )的图象在矩形 内部的部分均为自左向右下降时,直接写出 的取值范围.