吉林省长春市朝阳区2021年中考数学一模试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、单选题
-
1. 比 大1的数是( )A、 B、 C、 D、22. 空气中某种微粒的直径是0.00000297米,数据0.00000297用科学记数法可表示为( )A、 B、 C、 D、3. 如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式组 的解集为( )A、 B、 C、 D、5. 如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得 ,则树的高度 为( )
4. 不等式组 的解集为( )A、 B、 C、 D、5. 如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得 ,则树的高度 为( ) A、 B、 C、 D、6. 如图, 是⊙O的直径,点C、D在⊙O上,且在 异侧,连接 、 、 .若 ,则 的大小是( )
A、 B、 C、 D、6. 如图, 是⊙O的直径,点C、D在⊙O上,且在 异侧,连接 、 、 .若 ,则 的大小是( ) A、15° B、25° C、35° D、50°7. 如图,C是直线 外一点,按下列步骤完成作图:( )
A、15° B、25° C、35° D、50°7. 如图,C是直线 外一点,按下列步骤完成作图:( )⑴以点C为圆心,作能与直线 相交于D、E点的圆弧.
⑵分别以点D和点E为圆心, 长为半径作圆弧,两弧交于点F,连结 、 .
⑶作直线 交 于点G.
根据以上作图过程及所作图形,有如下结论:① ;② ;③ ;④ .其中正确的结论是( )
 A、①②③ B、①③④ C、③④ D、①④8. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )
A、①②③ B、①③④ C、③④ D、①④8. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )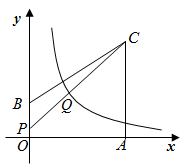 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 分解因式:a2+ab= .10. 已知a,b为两个连续的整数,且a< <b,则ba= .11. 若关于x的一元二次方程x2﹣4x+k=0有两个不相等的实数根,则k的值可以是(写出一个即可)12. 如图, 是正五边形 的对角线.若过点A作直线 ,则 的大小是度.
 13. 如图,在扇形 中,点B、C将 三等分,连结 、 ,⊙O的切线 交 的延长线于点E,过点B、C分别作 于点, 于点F.若 , ,则图中阴影部分图形的面积和为 . (结果保留π)
13. 如图,在扇形 中,点B、C将 三等分,连结 、 ,⊙O的切线 交 的延长线于点E,过点B、C分别作 于点, 于点F.若 , ,则图中阴影部分图形的面积和为 . (结果保留π) 14. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,抛物线 的顶点P在线段 上,与x轴相交于C、D两点,设点C、D的横坐标分别为 、 ,且 .若 的最小值是 ,则 的最大值是 .
14. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,抛物线 的顶点P在线段 上,与x轴相交于C、D两点,设点C、D的横坐标分别为 、 ,且 .若 的最小值是 ,则 的最大值是 .
三、解答题
-
15. 先化简,再求值: ,其中 , .16. 如图,三张不透明的卡片,正面图案分别是三张牛年生肖邮票,依次记为A、B、C,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀.小明从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求小明两次抽到图案上都是两头牛的生肖邮票的概率.
 17. 某学校需要购进甲、乙两种电脑,经调查,每台甲种电脑的价格比每台乙种电脑的价格少0.2万元,且用12万元购买的甲种电脑的数量与用20万元购买的乙种电脑的数量相同.求每台甲种电脑价格.18. 图①、图②、图③都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段 的端点和点O都在格点上.在图①、图②、图③中,分别以 为边画一个四边形,使点O到四边形的某两个顶点的距离相等,且所画图形的顶点都在格点上在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写出画法.
17. 某学校需要购进甲、乙两种电脑,经调查,每台甲种电脑的价格比每台乙种电脑的价格少0.2万元,且用12万元购买的甲种电脑的数量与用20万元购买的乙种电脑的数量相同.求每台甲种电脑价格.18. 图①、图②、图③都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段 的端点和点O都在格点上.在图①、图②、图③中,分别以 为边画一个四边形,使点O到四边形的某两个顶点的距离相等,且所画图形的顶点都在格点上在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写出画法. (1)、在图①中画一个四边形 ,使该四边形既是轴对称图形,又是中心对称图形,且点O在所画四边形的内部.(2)、在图②中画一个面积为16的四边形 ,使该四边形只是中心对称图形,且点O在所画四边形的内部.(3)、在图③中画一个四边形 ,使 ,且点O在所画四边形的边上.19. 某校为了解九年级360名学生周末在家体育锻炼的情况,在该校九年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了如下数据(单位:分钟)
(1)、在图①中画一个四边形 ,使该四边形既是轴对称图形,又是中心对称图形,且点O在所画四边形的内部.(2)、在图②中画一个面积为16的四边形 ,使该四边形只是中心对称图形,且点O在所画四边形的内部.(3)、在图③中画一个四边形 ,使 ,且点O在所画四边形的边上.19. 某校为了解九年级360名学生周末在家体育锻炼的情况,在该校九年级随机抽取了18名男生和18名女生,对他们周末在家的锻炼时间进行了调查,并收集得到了如下数据(单位:分钟)(收集整理数据)
男生:28,30,32,39,46,57,58,66,68,69,70,70,80,88,95,99,100,105
女生:29,35,36,48,55,56,62,69,69,72,73,78,88,88,90,98,99,109
(分析数据)两组数据的平均数、中位数、众数如下表:
统计量
数值
组别
平均数(单位:分钟)
中位数(单位:分钟)
众数(单位:分钟)
男生
66.7
68.5
a
女生
69.7
b
69.88
根据以上信息解答下列问题:
(1)、a= , b= .(2)、如果该校男、女生人数相同,估计该校九年级周末在家锻炼的时间在90分钟以上(不包含90分钟)同学的人数.(3)、王老师看了表格数据后认为九年级的女生周末锻炼做得比男生好,请你结合统计数据,写出两条支持王老师观点的理由.20. 如图, 是 的对角线,且 , 、 分别是边 、 的中线. (1)、求证:四边形 是菱形.(2)、若 , ,则点E、F之间的距离为 .21. 一艘轮船在航行中遇到暗礁船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,修船过程中进水和排水速度不变,修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽.设轮船触礁后船舱内积水量为 ,时间为 ,y与x之间的函数图象如图所示.
(1)、求证:四边形 是菱形.(2)、若 , ,则点E、F之间的距离为 .21. 一艘轮船在航行中遇到暗礁船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,修船过程中进水和排水速度不变,修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽.设轮船触礁后船舱内积水量为 ,时间为 ,y与x之间的函数图象如图所示. (1)、修船过程中排水速度为 ,a的值为 .(2)、求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.(3)、当船内积水量是船内最高积水量的 时,直接写出x的值.22. (教材呈现)如图是华师版八年级上册数学教材第79页的部分内容.
(1)、修船过程中排水速度为 ,a的值为 .(2)、求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.(3)、当船内积水量是船内最高积水量的 时,直接写出x的值.22. (教材呈现)如图是华师版八年级上册数学教材第79页的部分内容.
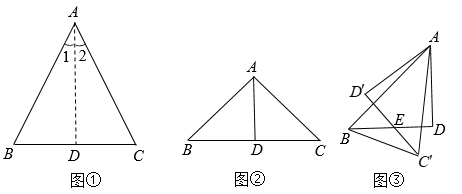 (1)、请根据教材分析,结合图①,写出完整的证明过程.
(1)、请根据教材分析,结合图①,写出完整的证明过程.(拓展)如图②, 是等腰直角三角形, , , 是边 的中线.将 绕着点A顺时针旋转角度 得到 ,连结 ,如图③.
(2)、设边 与边 相交于点E,若E为边 的中点,则 的长为 .(3)、连结 ,在整个旋转过程中, 面积的最大值为 .23. 如图,在 中, , , .动点P从点A出发,以每秒7个单位长度的速度沿折线 向终点B运动,当点P不与 顶点重合时,作 ,交边 于点Q,以 、 为边作 .设点P的运动时间为t秒. (1)、求 的长(2)、当点P在边 上时,求点Q到边 的距离(用含t的代数式表示)(3)、当 的某条对角线与 的直角边垂直时,求 的面积(4)、以点P为直角顶点作等腰直角三角形 ,使点E与点C在 同侧,设 的中点为F, 的对称中心为点O,连结 .当 时,直接写出t的值24. 在平面直角坐标系中,O为坐标原点,二次函数 ( ,且a为常数)的图象记为G.(1)、当点O在图象G上时,求a的值.(2)、当图象G的对称轴与直线 之间的部分的函数值y随x增大而减小时(直线 与对称轴不重合),求a的取值范围.(3)、当图象G的 部分的图象的最低点到x轴的距离是 部分图象的最低点到x轴的距离的2倍时,求a的值.(4)、以点 为对称中心,以 为边长作正方形,使该正方形的边与坐标轴平行或垂直.若图象G与该正方形的某条边只有两个交点,且两个交点之间的距离为 ,直接写出a的值.
(1)、求 的长(2)、当点P在边 上时,求点Q到边 的距离(用含t的代数式表示)(3)、当 的某条对角线与 的直角边垂直时,求 的面积(4)、以点P为直角顶点作等腰直角三角形 ,使点E与点C在 同侧,设 的中点为F, 的对称中心为点O,连结 .当 时,直接写出t的值24. 在平面直角坐标系中,O为坐标原点,二次函数 ( ,且a为常数)的图象记为G.(1)、当点O在图象G上时,求a的值.(2)、当图象G的对称轴与直线 之间的部分的函数值y随x增大而减小时(直线 与对称轴不重合),求a的取值范围.(3)、当图象G的 部分的图象的最低点到x轴的距离是 部分图象的最低点到x轴的距离的2倍时,求a的值.(4)、以点 为对称中心,以 为边长作正方形,使该正方形的边与坐标轴平行或垂直.若图象G与该正方形的某条边只有两个交点,且两个交点之间的距离为 ,直接写出a的值.