黑龙江省大庆市2021年中考数学二模试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、单选题
-
1. 实数a,b,c在数轴上的对应点的位置如图所示,那么这三个数中绝对值最大的是( )
 A、a B、b C、c D、无法确定2. 2020年5月,中科院沈阳自动化所主持研制的“海斗一号”万米海试成功,下潜深度超10900米,刷新我国潜水器最大下潜深度记录,将数据10900用科学记数法表示为( )A、 B、 C、 D、3. 若 ,则 的值为( )A、8 B、 C、9 D、4. 在函数 中,自变量x的取值范围是( )A、 B、 C、 D、 且5. 如图,在同一直角坐标系中,函数 与 的图象大致是( ).
A、a B、b C、c D、无法确定2. 2020年5月,中科院沈阳自动化所主持研制的“海斗一号”万米海试成功,下潜深度超10900米,刷新我国潜水器最大下潜深度记录,将数据10900用科学记数法表示为( )A、 B、 C、 D、3. 若 ,则 的值为( )A、8 B、 C、9 D、4. 在函数 中,自变量x的取值范围是( )A、 B、 C、 D、 且5. 如图,在同一直角坐标系中,函数 与 的图象大致是( ). A、①② B、①③ C、②④ D、③④6. 如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( )
A、①② B、①③ C、②④ D、③④6. 如图,是一个几何体的表面展开图,则该几何体中写“英”的面相对面上的字是( ) A、战 B、疫 C、情 D、颂7. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差8. 一个圆锥的底面直径是圆柱底面直径的3倍,如果它们的高相等,那么圆锥体积是圆柱体积的( )A、3倍 B、 C、9倍 D、9. 已知 ,则 的面积为( )A、6或 B、6或 C、12或 D、12或10. 如图,四边形 中,BC//AD, ,动点 从点 以每秒1个单位长度的速度向点 运动,动点 也同时从点 沿 的路线以每秒2个单位长度的速度向点 运动,当点 到达点 时,点 也随之停止运动,设点 运动的时间为 (单位:秒), 的面积为 ,当 时, 的值为( )
A、战 B、疫 C、情 D、颂7. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差8. 一个圆锥的底面直径是圆柱底面直径的3倍,如果它们的高相等,那么圆锥体积是圆柱体积的( )A、3倍 B、 C、9倍 D、9. 已知 ,则 的面积为( )A、6或 B、6或 C、12或 D、12或10. 如图,四边形 中,BC//AD, ,动点 从点 以每秒1个单位长度的速度向点 运动,动点 也同时从点 沿 的路线以每秒2个单位长度的速度向点 运动,当点 到达点 时,点 也随之停止运动,设点 运动的时间为 (单位:秒), 的面积为 ,当 时, 的值为( )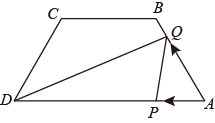 A、 或 B、3或 C、3或 D、 或
A、 或 B、3或 C、3或 D、 或二、填空题
-
11. 点 关于 轴对称的点 的坐标是 .12. 把多项式 分解因式的结果是 .13. 三角形的三边长分别是3cm,5cm,6cm,则连结三边中点所围成的三角形的周长是cm.14. 一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为 .
 15. 从﹣2,﹣1,2三个数中任取两个不同的数,作为点的坐标,则该点在第三象限的概率等于 .16. 如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有 盆花,每个图案中花盆总数为 ,按照图中的规律可以推断 与 的关系是 .
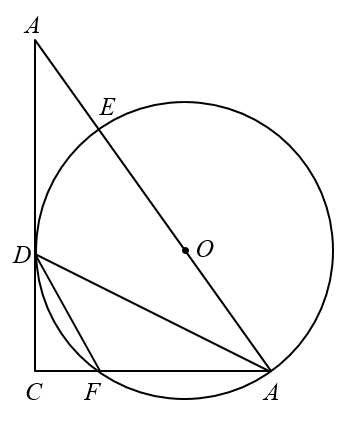
15. 从﹣2,﹣1,2三个数中任取两个不同的数,作为点的坐标,则该点在第三象限的概率等于 .16. 如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有 盆花,每个图案中花盆总数为 ,按照图中的规律可以推断 与 的关系是 . 17. 对于一元二次方程 ,有下列说法:①若 ,则 ;②若方程 有两个不相等的实根,则方程 必有两个不相等的实根;③若 是方程 的一个根,则一定有 成立;④若 是一元二次方程 的根,则 .其中说法正确的有(填序号).18. 如图,已知等腰三角形 于点 为 边中线, 相交于点 .在 从 减小到 的过程中,点 经过的路径长为 .
17. 对于一元二次方程 ,有下列说法:①若 ,则 ;②若方程 有两个不相等的实根,则方程 必有两个不相等的实根;③若 是方程 的一个根,则一定有 成立;④若 是一元二次方程 的根,则 .其中说法正确的有(填序号).18. 如图,已知等腰三角形 于点 为 边中线, 相交于点 .在 从 减小到 的过程中,点 经过的路径长为 .
三、解答题
-
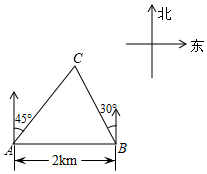
19. 计算: .20. 先化简,再求值: ,其中 .21. 解分式方程: .22. 如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从观测站A测得船C在北偏东45°的方向,从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.
 23. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
23. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
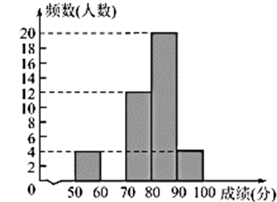
信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息解答下列问题:
(1)、补全第二组频数分布直方图(直接在图中补全);(2)、第三组竞赛成绩的众数是分,抽取的50名学生竞赛成绩的中位数是分;(3)、若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为人.24. 如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.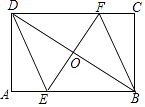 (1)、求证:四边形BEDF是平行四边形;(2)、当四边形BEDF是菱形时,求EF的长.25. 放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元,小贤要买3支笔芯,2本笔记本需花19元,小艺要买7支笔芯,1本笔记本需花费26元.(1)、求笔记本的单价和单独购买一支笔芯的价格;(2)、小贤和小艺都还想再买一件单价为3元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩2元钱,他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.(3)、当两人共同购买笔芯,享受整盒购买的优惠时,能让两人既买到各自的文具又都买到小工艺品.26. 如图,已知一次函数 的图象与反比例函数 的图象交于点 ,点 .
(1)、求证:四边形BEDF是平行四边形;(2)、当四边形BEDF是菱形时,求EF的长.25. 放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元,小贤要买3支笔芯,2本笔记本需花19元,小艺要买7支笔芯,1本笔记本需花费26元.(1)、求笔记本的单价和单独购买一支笔芯的价格;(2)、小贤和小艺都还想再买一件单价为3元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩2元钱,他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.(3)、当两人共同购买笔芯,享受整盒购买的优惠时,能让两人既买到各自的文具又都买到小工艺品.26. 如图,已知一次函数 的图象与反比例函数 的图象交于点 ,点 .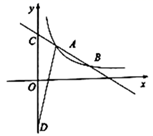 (1)、求反比例函数的表达式;(2)、若一次函数图象与y轴交于点C , 点D为点C关于原点O的对称点,求 的面积.
(1)、求反比例函数的表达式;(2)、若一次函数图象与y轴交于点C , 点D为点C关于原点O的对称点,求 的面积.