广东省惠州市2021年中考数学三模试卷
试卷更新日期:2021-07-13 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、 C、 D、2. 目前,我国“新冠”疫苗接种正在有序推进.国家卫生健康委员会公布的数据显示,截至2021年4月20日,全国各地累计报告接种新冠病毒疫苗已超过19500万剂次,将数据“19500万”用科学记数法可表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,是由五个相同的小立方块搭成的几何体,这个几何体的左视图是( )
4. 如图,是由五个相同的小立方块搭成的几何体,这个几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )A、7,9 B、9,9 C、8,9 D、9,86. 已知点 在反比例函数 的图象上,则点 关于原点对称的点的坐标是( )A、 B、 C、 D、7. 已知 ,则 的值为( )A、-12 B、12 C、9 D、-98. 不等式 的解集为( )A、x<-3 B、x≤2 C、-3<x≤2 D、无解9. 已知 ,相似比为 ,则 与 的面积比为( )A、 B、 C、 D、10. 如图是二次函数 ( , , 是常数, )图象的一部分,与 轴的交点 在点 和 之间,对称轴是直线 ,对于下列说法:① ;② ;③3 ;④当 时, ;⑤ (m为实数).其中正确的是( )
5. 在“美丽乡村”评选活动中,某乡镇7个村的得分如下:10,7,6,9,8,9,5,这组数据的中位数和众数分别是( )A、7,9 B、9,9 C、8,9 D、9,86. 已知点 在反比例函数 的图象上,则点 关于原点对称的点的坐标是( )A、 B、 C、 D、7. 已知 ,则 的值为( )A、-12 B、12 C、9 D、-98. 不等式 的解集为( )A、x<-3 B、x≤2 C、-3<x≤2 D、无解9. 已知 ,相似比为 ,则 与 的面积比为( )A、 B、 C、 D、10. 如图是二次函数 ( , , 是常数, )图象的一部分,与 轴的交点 在点 和 之间,对称轴是直线 ,对于下列说法:① ;② ;③3 ;④当 时, ;⑤ (m为实数).其中正确的是( ) A、①②③ B、①②⑤ C、②③④ D、③④⑤
A、①②③ B、①②⑤ C、②③④ D、③④⑤二、填空题
-
11. 因式分解: .12. 5的平方根是 .
13. 如图,已知 中, ,依据尺规作图的痕迹,则 . 14. 分式 有意义的x的取值范围是 .15. 图中圆心角 ,点 是弧 的中点,则 .
14. 分式 有意义的x的取值范围是 .15. 图中圆心角 ,点 是弧 的中点,则 . 16. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,点 、 、 是格点,则图中扇形 中阴影部分的面积是 .
16. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,点 、 、 是格点,则图中扇形 中阴影部分的面积是 .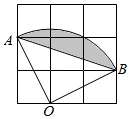 17. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,下列结论:① ;② ;③ ;④ .其中正确的结论是(填序号).
17. 如图,已知在正方形 中,对角线 与 相交于点 , , 分别是 与 的平分线, 的延长线与 相交于点 ,下列结论:① ;② ;③ ;④ .其中正确的结论是(填序号).
三、解答题
-
18. 计算: .19. 先化简,再求值. ,其中 .20. 已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.求证:四边形ABCD是平行四边形.
 21. 为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
21. 为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题: (1)、本次调查的学生人数是人;(2)、图2中α是度,并将图1条形统计图补充完整;(3)、请估算该校九年级学生自主学习时间不少于1.5小时有人;(4)、老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.22. 如图,AB为⊙O的直径,C、D是⊙O上的点,P是⊙O外一点, 于点E,AD平分 .
(1)、本次调查的学生人数是人;(2)、图2中α是度,并将图1条形统计图补充完整;(3)、请估算该校九年级学生自主学习时间不少于1.5小时有人;(4)、老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.22. 如图,AB为⊙O的直径,C、D是⊙O上的点,P是⊙O外一点, 于点E,AD平分 . (1)、求证:PD是⊙O的切线;(2)、若 , ,求⊙O的半径.23. 在今年的3月12日第43个植树节期间,某校组织师生开展了植树活动,在活动之前,学校决定购买甲、乙两种树苗,已知用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗比甲种树苗每棵少6元.(1)、求甲种树苗每棵多少元;(2)、若准备用7600元购买甲、乙两种树苗共200棵,则至少要购买乙种树苗多少棵?24. 如图,一次函数 与反比例函数 的图象相交于 , 两点,连接 , ,延长 交反比例函数图象于点 .
(1)、求证:PD是⊙O的切线;(2)、若 , ,求⊙O的半径.23. 在今年的3月12日第43个植树节期间,某校组织师生开展了植树活动,在活动之前,学校决定购买甲、乙两种树苗,已知用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗比甲种树苗每棵少6元.(1)、求甲种树苗每棵多少元;(2)、若准备用7600元购买甲、乙两种树苗共200棵,则至少要购买乙种树苗多少棵?24. 如图,一次函数 与反比例函数 的图象相交于 , 两点,连接 , ,延长 交反比例函数图象于点 . (1)、求一次函数 与反比例函数 的表达式;(2)、当 时,自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请求出点 的坐标.25. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)、求一次函数 与反比例函数 的表达式;(2)、当 时,自变量 的取值范围为;(3)、点 是 轴上一点,当 时,请求出点 的坐标.25. 如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D. (1)、填空:抛物线的解析式为;(2)、若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t,过点P作y轴的平行线交AC与M,当t为何值时,线段PM的长最大,并求其最大值;(3)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.
(1)、填空:抛物线的解析式为;(2)、若P是抛物线上位于直线AC上方的一个动点,设点P的横坐标为t,过点P作y轴的平行线交AC与M,当t为何值时,线段PM的长最大,并求其最大值;(3)、若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,请直接写出点E的坐标;若不能,请说明理由.