浙江省湖州市长兴县2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-12 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分) 下面每小题给出的四个选项中,只有一个是正确的,请选出各题中一个最符合题意的选项,不选、多选、错选的均不给分。
-
1. 在下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是( )A、3 B、-3 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 关于x的一元二次方程x2+kx-2=0(k为实数)根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5. 用配方法解一元二次方程x2-4x+1=0时,下列变形正确的是( )A、(x-2)2=1 B、(x-2)2=5 C、(x-2)2=3 D、(x+2)2=36. 小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )A、平均数 B、众数 C、加权平均数 D、中位数7. 下列说法错误的是( )A、平行四边形的对边相等 B、对角线互相垂直的平行四边形是菱形 C、对角线相等的四边形是矩形 D、正方形既是轴对称图形、又是中心对称图形8. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒。若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )
2. 已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是( )A、3 B、-3 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 关于x的一元二次方程x2+kx-2=0(k为实数)根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定5. 用配方法解一元二次方程x2-4x+1=0时,下列变形正确的是( )A、(x-2)2=1 B、(x-2)2=5 C、(x-2)2=3 D、(x+2)2=36. 小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )A、平均数 B、众数 C、加权平均数 D、中位数7. 下列说法错误的是( )A、平行四边形的对边相等 B、对角线互相垂直的平行四边形是菱形 C、对角线相等的四边形是矩形 D、正方形既是轴对称图形、又是中心对称图形8. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒。若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( ) A、(30-2x)(40-x)=600 B、(30-2x)(40-2x)=600 C、(30-x)(40-2x)=600 D、(30-x)(40-x)=6009. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,2 ),反比例函数y= (k<0)的图象与菱形对角线AO交于点D,连结BD,当DB⊥x轴时,k的值是( )
A、(30-2x)(40-x)=600 B、(30-2x)(40-2x)=600 C、(30-x)(40-2x)=600 D、(30-x)(40-x)=6009. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,2 ),反比例函数y= (k<0)的图象与菱形对角线AO交于点D,连结BD,当DB⊥x轴时,k的值是( ) A、 B、 C、 D、10. 如图,已知四边形ABCD是边长为4的正方形,以对角线BD为边作正三角形BDE,过点E作EF⊥DA,交DA的延长线于点F,则AF的长是( )
A、 B、 C、 D、10. 如图,已知四边形ABCD是边长为4的正方形,以对角线BD为边作正三角形BDE,过点E作EF⊥DA,交DA的延长线于点F,则AF的长是( )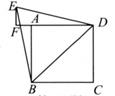 A、2 -2 B、2 -2 C、 -1 D、
A、2 -2 B、2 -2 C、 -1 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 若二次根式 在实数范围内有意义,则x的取值范围为12. 正五边形的外角和等于13. 数据1,8,8,4,6,4的中位数为14. 如图,在 ABCD中,BE平分∠ABC,BC=3,DE=1,则 ABCD的周长是
 15. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE=
15. 如图,在矩形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME=15°,则∠ABE= 16. 如图,在平面直角坐标系中,四边形ABCD是矩形,已知点A(0,2),AB=2AD,点C,D在反比例函数y= (k>0)的图象上,AB与x轴的正半轴相交于点E,若点E为AB的中点,则k的值为
16. 如图,在平面直角坐标系中,四边形ABCD是矩形,已知点A(0,2),AB=2AD,点C,D在反比例函数y= (k>0)的图象上,AB与x轴的正半轴相交于点E,若点E为AB的中点,则k的值为
三、解答题(本题共有8小题,共66分)
-
17. 计算:18. 解方程:x2-2x-3=019. 一次函数y=2x+2与反比例函数y= (k≠0)的图象都经过点A(1,m),y=2x+2的图象与x轴交于点B。(1)、求点B的坐标及反比例函数的表达式;(2)、点C(0,-2),若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上。20. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE。

求证:
(1)、BE=DE。(2)、四边形BEDF是菱形。21. 某市篮球队到市一中选拔一名队员. 教练对甲和乙两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数。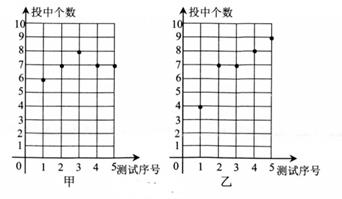 (1)、你认为谁的成绩比较稳定,为什么?(2)、若你是教练,你打算选谁?简要说明理由。22. 如图,在平面直角坐标系中,过点M (0,2)的直线l与x轴平行,且直线l分别与反比例函数y= (x> 0)和y= (x< 0)的图象交于点P,点Q。
(1)、你认为谁的成绩比较稳定,为什么?(2)、若你是教练,你打算选谁?简要说明理由。22. 如图,在平面直角坐标系中,过点M (0,2)的直线l与x轴平行,且直线l分别与反比例函数y= (x> 0)和y= (x< 0)的图象交于点P,点Q。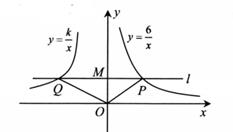 (1)、求点P的坐标;(2)、若△POQ的面积为7,求k的值。23. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为5万元,设可变成本平均每年增长的百分率为x。(1)、用含x的代数式表示第3年的可变成本为万元。(2)、如果该养殖户第3年的养殖成本为11.2万元,求可变成本平均每年增长的百分率。24. 反比例函数y1= (x>0,k≠0)的图象经过点(1,3),点P是一次函数y2=-x+6图象上的一个动点,如图所示,设点P的横坐标为m,且满足-m+6> ,过点P分别作PB⊥x轴,PA⊥y轴,垂足分别为B,A,与反比例函数分别交于D,C两点,连结OC,OD,CD.
(1)、求点P的坐标;(2)、若△POQ的面积为7,求k的值。23. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为5万元,设可变成本平均每年增长的百分率为x。(1)、用含x的代数式表示第3年的可变成本为万元。(2)、如果该养殖户第3年的养殖成本为11.2万元,求可变成本平均每年增长的百分率。24. 反比例函数y1= (x>0,k≠0)的图象经过点(1,3),点P是一次函数y2=-x+6图象上的一个动点,如图所示,设点P的横坐标为m,且满足-m+6> ,过点P分别作PB⊥x轴,PA⊥y轴,垂足分别为B,A,与反比例函数分别交于D,C两点,连结OC,OD,CD. (1)、求k的值并结合图象求出m的取值范围;(2)、在点P运动过程中,若BD=2PD,求点P的坐标;.(3)、将△OCD沿着直线CD翻折,点0的对应点为点O',得到四边形O'COD,问:四边形O'COD能否为菱形?若能,求出点P坐标;若不能,说明理由。
(1)、求k的值并结合图象求出m的取值范围;(2)、在点P运动过程中,若BD=2PD,求点P的坐标;.(3)、将△OCD沿着直线CD翻折,点0的对应点为点O',得到四边形O'COD,问:四边形O'COD能否为菱形?若能,求出点P坐标;若不能,说明理由。