浙江省湖州市南浔区 2020 -2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-12 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 如图，已知射线BA，BC被直线EF所截，图中的∠1与∠2是（）

A、对顶角 B、同位角 C、内错角 D、同旁内角

查看试题解析
2. 浔浔家今年1 -5月份的用电量情况如图所示，则浔浔家月用电量最大的是（）

A、2月 B、3月 C、4月 D、5月

查看试题解析
3. 华为下一代麒麟处理器，将会被命名为麒麟9020，采用全新3nm（纳米）工艺制程3纳米=0.000000003米，将0.000000003用科学记数法表示为（）

A、3×10^-8 B、3×10^-9 C、0.3×10^-8 D、-3×109

查看试题解析
4. 下列计算正确的是（）

A、a²+a²=a⁴ B、a²·a³=a⁶ C、a⁵÷a²=a³ D、（a²）³=a⁵

查看试题解析
5. 如图，将一块三角板的直角顶点放在直尺的一边上。当∠1=50°时，则∠2的度数为（）

A、25° B、40° C、50° D、130°

查看试题解析
6. 当x=1时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x + 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x - 1}$

查看试题解析
7. 下列多项式中，能用完全平方公式进行分解因式的是（）

A、4x²-1 B、x²-2x-1 C、4x²+2x+ 1 D、4x²-4x+1

查看试题解析
8. 已知 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ 是二元一次方程组 ${\begin{cases} 2 a x + b y = 1 \\ a x - 2 b y = 3 \end{cases}$ 的解，则a-3b的值为（）

A、-2 B、2 C、-4 D、4

查看试题解析
9. 《九章算术》中，一次方程组是由算筹布置而成的。如图1所示的算筹图，表示的方程组，就是 ${\begin{cases} 2 x + y = 11 \\ 4 x + 3 y = 27 \end{cases}$ ，类似地，图2所示的算筹图表示的方程组为（）

A、 ${\begin{cases} 3 x + 2 y = - 14 \\ x + 4 y = 23 \end{cases}$ B、 ${\begin{cases} 3 x + 2 y = - 9 \\ x + 4 y = 23 \end{cases}$ C、 ${\begin{cases} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{cases}$ D、 ${\begin{cases} 3 x + 2 y = 19 \\ x + 4 y = 3 \end{cases}$

查看试题解析
10. 已知a₁=x+1（x≠0且x≠1），a₂= $\frac{1}{1 - a_{1}}$ ，a₃= $\frac{1}{1 - a_{2}}$ ……，a_n= $\frac{1}{1 - a_{n - 1}}$ ，则a₂₀₂₁等于（）

A、-x+1 B、x+1 C、 $\frac{1}{x + 1}$ D、 $- \frac{1}{x}$

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 分解因式：m²-4=

查看试题解析
12. 如图是某校参加各兴趣小组的学生人数分布扇形统计图，已知参加STEAM课程兴趣小组的人数为100人．则该校参加各兴趣小组的学生其有人

查看试题解析
13. 如图，已知AB∥CD，∠1=50°，则∠3的度数是

查看试题解析
14. 化简 $\frac{a^{2}}{a - b} + \frac{b^{2}}{b - a}$ 的正确结果是

查看试题解析
15. 我们知道，同底数幂的乘法法则为a^m·aⁿ=a^m+n（其中a≠0，m、n为正整数），类似地我们规定关于任意正整数m、n的一种新运算：h（m+n）=h（m） ·h（n）；比如h（2）=5，则h（4）=h（2+2）=5×5=25．若h（3）=k（k≠0）。则h（3b）·h（27）（其中b为正整数）的结果是。

查看试题解析
16. 建党100周年主题活动中，702班浔浔设计了如图1的“红色徽章"．其设计原理是：如图2，在边长为a的正方形EFCH四周分别放置四个边长为b的小正方形，构造了一个大正方形ABCD，并画出阴影部分图形，形成了“红色徽章"的图标现将阴影部分图形面积记作S₁ ，每一个边长为b的小正方形面积记作S₂ ．若S₁=6S₂ ，则 $\frac{a}{b}$ 的值是

查看试题解析

三、解答题（本题有8个小题，共52分）

17. 计算：

(1)、2^-2-（ $\frac{2}{3}$ ）⁰

(2)、（-xy²）（xy）³

查看试题解析
18. 解方程（组）：

(1)、 ${\begin{cases} 3 x - y = - 7 \\ x + 3 y = 1 \end{cases}$

(2)、 $\frac{x}{x - 1} - \frac{2}{1 - x} = 2$

查看试题解析
19. 先化简．再求值： $(\frac{3 x}{x - 1} - \frac{x}{x + 1}) \cdot \frac{x^{2} - 1}{x}$ ，其中x=-2

查看试题解析
20. 如图，已知每个小正方形的边长为1，且正方形的顶点称为格点，网格中有一只小鱼，若小鱼平移游动，平移后的鱼头部分已画出（鱼身顶点都在格点上）

(1)、请作出请补全平移后的鱼尾部分△A₁B₁C₁；

(2)、若格点P满足S△_PAB=S_△ABC ，请在网格中标出一个满足条件的点P。
（温馨提示：请画在答题卷相对应的图上）

查看试题解析

21. 为庆祝建党100周年，某学校组织党建知识竞赛，随机抽取部分同学的成绩进行统计，制作如下频数分布表和频数分布直方图．请根据图表中提供的信息，解答下列问题：

党建知识竞赛成绩频数分布表

成绩x/分	频数	频率
70≤x<80	6	0.15
80≤x<90	8	m
90≤x<100	n	0.3
100≤x<110	8	0.2
l10≤x<120.	6	0.15

党建知识竞赛成绩频数分布直方图

(1)、该校随机抽取了多少名学生成绩进行统计？

(2)、求m，n的值，并补全频数分布直方图；（温馨提示：请画在答题卷相对应的图上）

(3)、若该校学生共有1000人，请估计该校分数在100≤x<120的学生有多少人？

查看试题解析

22. 我们通常用作差法比较代数式大小例如：已知M=2x+3，N=2x+1。比较M和N的大小先求M-N，若M-N>0，则M>N；若M-N<0，则M<N；若M-N=0，则M=N，反之亦成立。本题中因为M-N=2x+3-（2x+1）=2>0，所以M>N。

(1)、如图1是边长为a的正方形，将正方形一边不变，另一边增加4，得到如图2所示的新长方形，此长方形的面积为S₁；将图1中正方形边长增加2得到如图3所示的新正方形。此正方形的面积为S₂
①用含a的代数式分别表示S₁和S₂（结果需要化简）；

②请用作差法比较S₁与S₂大小

(2)、若M=a² ， N=4-（a+1）² ，且M=N，求a（a+1）的值。

查看试题解析

23. 某单位计划采购包装盒，有A、B两种产品可供选择，已知每个A产品的单价比每个B产品的单价少10元，且用1400元买到4产品数量与用1600元买到B产品数量一样多

(1)、A、B两种产品单价各是多少元？

(2)、恰逢商家促销活动，该单位调查了甲，乙两商家，了解到的信息如下表：

产品商家	A产品		B产品
甲商家	不超过5件	超出5件的部分	打六折销售
	按原标价销售	打八折销售
乙商家	两种产品的标价与折扣前标价相同，但买一个B产品赠送一个A产品

现单位计划买10个A产品和4个B产品，若想使总花费最少。请通过计算分析应选择怎样的方案进行购买？并求出此时的最少总费用。

查看试题解析

24. 如图，直线MN∥PQ。将一副三角板中的两块直角三角板如图1放置，∠ACB=∠EDF=90°，∠ABC=∠BAC=45°，∠DFE=30°，∠DEF=60°，此时，点A与点E重合。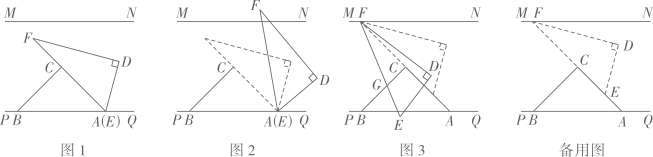

(1)、对于图1，固定△ABC的位置不变，将△DEF绕点E按顺时针方向进行旋转，旋转至DE与BC首次平行，如图2所示，求此时∠FAC的度数。

(2)、对于图1，固定△ABC的位置不变，将△DEF沿AC方向平移至点F正好落在直线MN上，再将ODEF绕点F按顺时针方向进行旋转，如图3所示。
①若边EF与边BC交于点C，试判断∠BGF-∠EFN的值是否为定值。若是定值，则求出该定值。若不是定值。请说明理由；

②对于图3，固定△ABC的位置不变，将△DEF绕点F顺时针方向以每秒10°的速度进行旋转，当EF与直线MN首次重合时停止运动．当经过1秒时。线段DE与△ABC的一条边平行，求满足条件的t的值。

查看试题解析

四、自选题（本题有2个小题，共5分）

25. 定义一种新的运算：a☆b=2a-b，例如：3☆（-1）=2×3-（-1）=7。若a☆b=0，且关于x，y的二元一次方程（a+1）x-by-a+3=0，当a，b取不同值时，方程都有一个公共解，那么这个公共解为

查看试题解析
26. 某商场在一楼至二楼间安装了一部自动扶梯，以匀速向上行驶。甲，乙两同学同时从扶梯上匀速走到二楼，且甲每分钟走动的级数是乙的两倍。已知甲走了24级到扶梯顶部，乙走了16级到扶梯顶部（甲、乙两同学每次只跨一级台阶）

(1)、扶梯露在外面的部分有多少级？

(2)、如果与扶梯并排有一从二楼到一楼的楼梯道，台阶数与扶梯级数相同，甲、乙各自到扶梯顶部后按原速再下楼梯到楼梯底部再乘扶梯，若楼梯与扶梯之间的距离忽略不计，问甲第1次追上乙时是在扶梯上还是在楼梯上？他已经走动的级数是多少级？

查看试题解析