四川省乐山市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-12 类型：期末考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 点（-2，0）在（）

A、x轴上 B、y轴上 C、第二象限 D、第四象限

查看试题解析
2. 已知ABCD是平行四边形，以下说法不正确的是（）

A、其对边相等 B、其对角线相互平分 C、其对角相等 D、其对角线互相垂直

查看试题解析
3. 若a，b的值均扩大为原来的2倍，则下列分式的值保持不变的是（）

A、 $\frac{a}{a + b}$ B、 $\frac{a^{2}}{a + b}$ C、 $\frac{a^{2}}{2 b}$ D、 $\frac{3 a^{2}}{2 b^{3}}$

查看试题解析
4. 如图，在平行四边形ABCD中，∠DBC=25°，∠BAD=115°，则∠BDC=（）

A、25° B、30° C、40° D、65°

查看试题解析
5. 在植树节活动中，某单位组织职工开展植树竞赛，下图反映的是植树量与人数之间的关系。根据图中信息可知，参与本次活动的人数为（）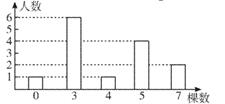

A、19 B、17 C、14 D、56

查看试题解析
6. 下列函数中，图象经过一、二、四象限的是（）

A、y=2x-1 B、y=-2x+1 C、y= $\frac{2}{x}$ D、y= $- \frac{2}{x}$

查看试题解析
7. 小王的账户现有存款a元，每月支出b元，收入c元（a、b、c都是常数，且都大于0），则小王账户的余额与所存月数的函数图象可能是下列图形中的（）

A、②③ B、②④ C、③④ D、②③④

查看试题解析
8. 如图，在菱形ABCD中，AB=5、AC= 8，则该菱形的面积为（）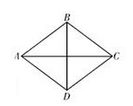

A、40 B、20 C、48 D、24

查看试题解析
9. 已知点A（-1，y₁），B（2，y₂），C（-3，y₃）都在反比例函数y= $\frac{- m^{2} - 1}{x}$ 的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃>y₁>y₂ B、y₁>y₃>y₂ C、y₂>y₁>y₃ D、y₂>y₃>y₁

查看试题解析
10. 小王从甲地到相距50千米的乙地办事，乘出租车去，乘公共汽车回来．已知出租车的平均速度比公共汽车的平均速度快15千米/小时，去时路上所用的时间比返回时少了 $\frac{1}{3}$ 。设公共汽车的平均速度为x千米/小时，则下面列出的方程中，正确的是（）

A、 $\frac{50}{x + 15} = \frac{2}{3} \times \frac{50}{x}$ B、 $\frac{50}{x} = \frac{2}{3} \times \frac{50}{x + 15}$ C、 $\frac{50}{x + 15} + \frac{1}{3} = \frac{50}{x}$ D、 $\frac{50}{x} = \frac{50}{x + 15} - \frac{1}{3}$

查看试题解析
11. 如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在边AD上的点F处，若AB=4，BC=5，则AE的长为（）

A、 $\frac{4}{3}$ B、 $\frac{5}{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{4}$

查看试题解析
12. 如图，反比例函数y= $\frac{k}{x}$ （k>0）的图象经过矩形0ABC对角线的交点D，分别交AB、BC于点E、F。若四边形OEBF的面积为6，则k的值为（）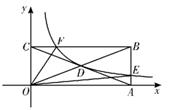

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分。

13. 一组数据：-1，2，x，4，5的众数是5，则这组数据的中位数为。

查看试题解析
14. 当函数y=6-2x的函数值取值为2时，自变量x的取值是。

查看试题解析
15. 小王在文具店以0.5元/只的价格买了m只3B铅笔，又以0.8元/只的价格买了n只4B铅笔，那么小王所买铅笔的平均价格为元/只。

查看试题解析
16. 某单位组织职工对某地进行绿化，已知绿化面积S（m²）与工作时间t（h）之间的函数关系如图所示，则4小时结束时，绿化面积为m²。

查看试题解析
17. 如图，菱形ABCD中，AB=4，∠ABC=120°，过对角线AC延长线上的一点P分别作AD、DC延长线的垂线，垂足分别为E、F，则PE-PF= 。

查看试题解析
18. 如图，在平面直角坐标系中，0为坐标原点，点A的坐标为（0，8），点B的坐标为（-4，0），点P是直线l：x+y=4上的一个动点，若∠PAB=∠ABO，则点P的坐标是。

查看试题解析

三、本大题包含第19题、20题、21题，共3小题，每小题8分，共24分．

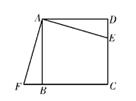
19. 计算2⁵×4^-2-（-1）²⁰²¹-π⁰÷2^-1

查看试题解析
20. 解方程： $\frac{2}{x} = \frac{3}{x - 1}$

查看试题解析
21. 如图，在正方形ABCD中，E是CD上一点，F是CB延长线上一点。若DE=BF，求证：∠EAF=90°。

查看试题解析

四、本大题包含第22题、23题、24题，共3小题，每小题9分，共27分。

22. 已知b=2a≠0，计算 $\frac{1}{2 a} - \frac{1}{a + b} \cdot (\frac{a + b}{2 a} - a + b)$

查看试题解析
23. 在矩形ABCD中，AB=3，AD=9，对角线AC、BD交于点O，一直线过O点分别交AD、BC于点E、F，且ED=4，求证：四边形AFCE为菱形。

查看试题解析
24. 已知P（2，n）为反比例函数y= $\frac{4}{x}$ （x>0）图象上的一点．将直线y=-2x沿x轴向右平移过点P时，交x轴于点Q，若点M为y轴上一个动点，求PM+QM的最小值。

查看试题解析

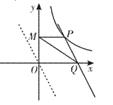
五、本大题包含第25题、26题，共2小题，每小题10分，共20分。

25. 如图，在同一坐标系中，直线l₁：y=-x+2交x轴于点P，直线l₂：y=ax-4过点P。

(1)、求a的值；

(2)、点M、N分别在直线l₁ ， l₂上，且关于原点对称，求△PMN的面积。

查看试题解析

26. 为了从甲、乙两名选手中选拔一人参加射击比赛，现对他们进行一次测验，两人在相同条件下各射靶10次，为了统计他们的成绩，制作了如下统计图表：

甲、乙射击成绩统计表

	平均数	中位数	方差	命中10环的次数
甲	7			0
乙				1

甲、乙射击成绩折现图

(1)、请补全，上述统计图表和折线图；

(2)、如果规定成绩较稳定者胜出，你认为谁应胜出？为什么？

(3)、如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？

查看试题解析

六、本大题共2小题，第27题12分，第28题13分，共25分．

27. 在菱形ABCD中，∠ADC=60°，点F为CD上任意一点（不与C、D重合），过点F作CD的垂线，交BD于点E，连结AE。

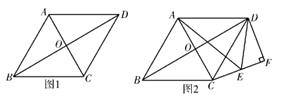(1)、①依题意补全图1；
②写出线段EF、CF、AE之间得等量关系，并说明理由；

(2)、在图1中，将△DEF绕点D逆时针旋转，当F、E、C在一条直线上，如图2所示，请判断EF、CE、AE之间的等量关系，写出判断思路（可以不写出证明过程）．

查看试题解析
28. 如图，已知直线y=-2x与双曲线y= $\frac{k}{x}$ （k<0）上交于A、B两点，且点A的纵坐标为-2

(1)、求k的值；

(2)、若双曲线y= $\frac{k}{x}$ （k<0）上一点C的纵坐标为 $\frac{1}{2}$ ，求△BOC的面积；

(3)、若A、B、P、Q为顶点组成的四边形为正方形，直接写出过点P的反比例函数解析式。

查看试题解析