广西防城港市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-12 类型：期末考试

进入 出卷网 下载

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑。）

  • 1. 下列各数中，属于无理数的是（    ）
    A、13 B、3 C、π D、1

    查看试题解析

  • 2. 下列调查中，适合采用抽样调查方式的是（    ）
    A、了解新冠肺炎确诊病人同机乘客的健康情况 B、调查某中学在职教师的身体健康状况 C、疫情期间对全校同学进行每日温度测量统计 D、中央电视台《开学第一课》的收视率调查

    查看试题解析

  • 3. 如图，若∠1+∠2=220°，则∠3的度数为（    ）

    A、70° B、60° C、65° D、50°

    查看试题解析

  • 4. 某学校领导想了解本校七年级800名学生的学习情况，从中抽取七年级200名学生的期中考试成绩进行统计，在这个问题中，样本容量是（    ）
    A、800 B、200 C、600 D、1000

    查看试题解析

  • 5. 下列运算不正确的是（    ）
    A、32 =3 B、(2)2 =2 C、−83 =-2 D、16 =±4

    查看试题解析

  • 6. 如果点P（m+3，m）在直角坐标系的x轴上，那么P点坐标为（    ）
    A、（3，0） B、（0，3） C、（0，-3） D、（-3，0）

    查看试题解析

  • 7. 若m>n，则下列不等式正确的是（   ）
    A、m-2<n-2 B、m4>n4 C、6m<6n D、-8m>-8n

    查看试题解析

  • 8. 不等式组 {x+1≤4x−2<3(x+1) 的解集在数轴上表示正确的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 9. 用代入消元法解方程组 {3x−y=2 ， ①y=1−2x ， ② 时，把②代入①，得（   ）
    A、3x-1-2x= 2 B、3x-（1-2x）= 2 C、3x+（1-2x）=2 D、3（1-2x）-y=2

    查看试题解析

  • 10. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（    ）

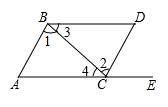    A、∠1=∠2 B、∠3=∠4 C、∠D=∠DCE D、∠D+∠ACD=180°

    查看试题解析

  • 11. 如图所示，在三角形ABC中，AC⊥BC，CD⊥AB，垂足分别是C，D，那么以下线段大小的比较必定成立的是（    ）

    A、CD>AD B、AC<BC C、BC>BD D、CD<BD

    查看试题解析

  • 12. 对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到“判断结果是否大于190？”为一次操作，如果操作恰好进行两次就停止了，那么x的取值范围是（   ）

    A、8<x≤22 B、8≤x<22 C、8<x≤64 D、22<x≤64

    查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分． ）

  • 13. 平面直角坐标系中，点A（2，3）在第象限。

    查看试题解析

  • 14. 把方程2x+y-7=0改写成用含x的式子表示y，则y= 。

    查看试题解析

  • 15. 用吸管吸易拉罐内的饮料时，如图，∠1=100°，则∠2=。（易拉罐的上下底面互相平行）

    查看试题解析

  • 16. 点P位于x轴下方，y轴左侧，距离x轴4个单位长度，距离y轴2个单位长度，那么P的坐标是。

    查看试题解析

  • 17. 已知（m-1）x|m|+3>0是关于x的一元一次不等式，则m的值为。

    查看试题解析

  • 18. 将1， 2 ， 3 ， 6 按如图方式排列．若规定（m，n）表示第m排从左向右第n个数，如（5，4）表示的数是 2 （即第5排从左向右第4个数），那么（2021，1011）。所表示的数是。

    查看试题解析

三、解答题（本大题共8小题，共66分，解答应写出文字说明、证明过程或演算步骤。）

  • 19. 计算： (2+3)−(3−2)

    查看试题解析

  • 20. 解不等式 3x+14−1≤x−12 ，并在数轴上表示解集。

    查看试题解析

  • 21. 解方程组： {x−3y=3 ， ①x+y=15 ， ②

    查看试题解析

  • 22. 如图，三角形ABC可以记为△ABC，它的三个顶点A，B，C都在小正方格的格点上，现将△ABC向左平移5个单位长度，再向下平移6个单位长度得到△A1B1C1 ， 其中点A，B，C的对应点为A1 ， B1 ， C1

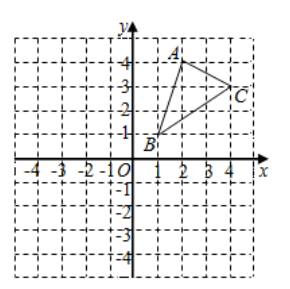    (1)、画出平移后得到的△A1B1C1；
    (2)、写出A1 ， B1两点的坐标；
    (3)、在图中连接AA1和CC1 ， 则这两条线段之间有什么关系？（直接回答，不需要说明理由）

    查看试题解析

  • 23. 小李调查了本班50名同学各自家庭的人均日用水量（单位：升）

    收集数据如下：

    55  42  50  48  42  35  38  39  40  51  47  52  50  42  43  47  52  48 

    52  38  42  60  52  41  46  35  47  53  48  52  47  50  49  57  43  40

    44  52  50  49  37  46  42  62  58  46  48  39  60  54

    整理数据：列频数分 布表如下（不完整）

    组别

    人均日用水量（x）

    划记

    频数（家庭数）

    A

    35≤x＜39

    5

    B

    39≤x＜43

    10

    C

    43≤x＜47

    6

    D

    47≤x＜51

    14

    E

    51≤x＜55

    9

    F

    55≤x＜59

    		    

    G

    59≤x＜63

    3

    合计

    50

    50

    描述数据：画频数分布直方图和扇形统计图如右图

    根据以上信息，解答下列问题：

    (1)、请分别补全频数分布表、频数分布直方图和扇形统计图；
    (2)、求D组数据所对应的扇形统计图的圆心角度数；
    (3)、①家庭的人均日用水量在哪个范围的频数最多？

    ②小李为了在班级上提倡节约用水，而且使班级中70%的家庭不受影响，他应该倡议家庭的人均日用水量不超过多少升比较合适？（取正整数值，不用说明理由）

    查看试题解析

  • 24. 为了响应“足球进校园”的号召，某校计划为学校足球队购买一批足球，已知在某商店购买4个A品牌的足球和2个B品牌的足球共需680元，购买2个A品牌的足球和3个B品牌的足球共需540元
    (1)、求A，B两种品牌的足球的单价；
    (2)、“五一”期间，该商店对足球进行打折促销，其中A品牌打八折，B品牌打九折，学校打算购买15个A品牌的足球和4个B品牌的足球，问学校购买这批打折后的足球所花的费用比打折前节省了多少钱？

    查看试题解析

  • 25. 已知：如图，在△ABC中，点D，E，F，G分别在线段AB，AC，DG，BC上，且∠5=∠C，∠3=∠B。

    (1)、求证：DE∥BC；
    (2)、判断：∠4与∠B相等吗？为什么？
    (3)、求证：∠1=∠2

    查看试题解析

  • 26. 如图，在平面直角坐标系中，AB∥CD∥x轴，BC∥DE∥y轴，且AB=CD=4cm，OA=5cm，DE=2cm，动点P从点A出发，以每秒1cm的速度，沿ABC路线向点C运动；动点Q从点O出发，以每秒2cm的速度，沿OED路线向点D运动。若P，Q两点同时出发，其中一点到达终点时，则两点同时停止运动。

    (1)、直接写出OE，BC的长度；
    (2)、求P，Q两点从开始出发到停止运动用了多少秒钟？
    (3)、若P，Q两点出发3秒后立即同时停止．①请在备用图中画出此时的△PQC；②求△PQC的面积；

    查看试题解析