浙江省温州市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-12 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 如图，直线a，b被直线l所截，∠1与∠2是一对（）

A、同位角 B、内错角 C、对顶角 D、同旁内角

查看试题解析
2. 下列方程中，属于二元一次方程的是（）

A、x²-y=1 B、x+ $\frac{1}{y}$ =2 C、2x+y=3z D、2x+ $\frac{y}{3}$ =4

查看试题解析
3. 在下列从左到右的变形中，不是因式分解的是（）

A、x²-x=x（x-1） B、x²+3x-1=x（x+3）-1 C、x²-y²=（x+y）（x-y） D、x²+2x+1=（x+1）²

查看试题解析
4. 新冠病毒由蛋白质外壳和单链核酸组成，直径大约在60~140纳米（1纳米=00000001厘米）。某冠状病毒的直径约0.0000135厘米。数据“0.0000135”用科学记数法表示为（）

A、1.35×10^-6 B、13.5×10^-6 C、1.35×10^-5 D、0.135×10^-4

查看试题解析
5. 下列调查中，应作全面调查的是（）

A、日光灯管厂要检测一批灯管的使用寿命 B、了解居民对废电池的处理情况 C、了解现代大学生的主要娱乐方式 D、某公司对退休职工进行健康检查

查看试题解析
6. 下列运算正确的是（）

A、a²·a³=a⁶ B、a⁵÷a²=a³ C、（ab）²=ab² D、（a+3）²=a²+9

查看试题解析
7. 某养猪场对200头生猪的质量进行统计，得到频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，其中质量在82.5kg及以上的生猪有（）

A、20头 B、50头 C、140头 D、200头

查看试题解析
8. 要使分式 $\frac{a^{2} - 4}{a^{2} - 4 a + 4}$ 有意义，实数a必须满足（）

A、a=2 B、a=-2 C、a≠2 D、a≠2且a≠-2

查看试题解析

9. 下表中的每一对x，y的值都是二元一次方程ax+by=10的一个解，则下列结论中正确的是（）

x	……	-3	-2	-1	0	1	2	3	……
y	……	13	12	11	10	9	8	7	……

A、当x<0时，y的最小值是10 B、当y<10时，x的最小值是1 C、当x取任何实数时，均有y≥0 D、当x的值越来越大时，y的值越来越小

查看试题解析

10. 将边长为m的三个正方形纸片按如图1所示摆放并构造成边长为n的大正方形时，三个小正方形的重叠部分是两个边长均为1的正方形；将其按如图2所示摆放并构造成一个邻边长分别为3m和n的长方形时，所得长方形的面积为35。则图2中长方形的周长是（）

A、24 B、26 C、28 D、30

查看试题解析

二、填空题（本题有8题，每小题3分，共24分）

11. 因式分解：m²+2m=

查看试题解析
12. 计算： $\frac{7 a}{6 b^{2}} \cdot \frac{12 b^{2}}{7 a^{2}}$ =

查看试题解析
13. 某班级有45名学生在期中考试学情分析中，分数段在70~79分的频率为0.4，则该班级在这个分数段内的学生有人

查看试题解析
14. 已知方程组 ${\begin{cases} x + 2 y = 7 \\ 2 x + y = 2 \end{cases}$ ，则x+y的值是

查看试题解析
15. 一副三角尺ABC， DEF拼接成如图所示的图形，其中∠B=30°∠D=45°，DF经过点A，两斜边AB与DE互相平行，则∠CAF= 度

查看试题解析
16. 若x²-nx-6=（x-2）（x+3），则常数n的值是

查看试题解析
17. 如图，在长方形ABCD中，AB=3，BC=6，现将它先向上平移2个单位，再向右平移1个单位得到长方形A'B'C'D'，连结CC'，则图中阴影部分的面积是

查看试题解析
18. 如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成，在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行．当∠EFH=55°，BC∥EF时，∠ABC=度；如图3，为了参与另外一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF所在直线互相垂直，且∠EFH=78°，则这时∠ABC= 度

查看试题解析

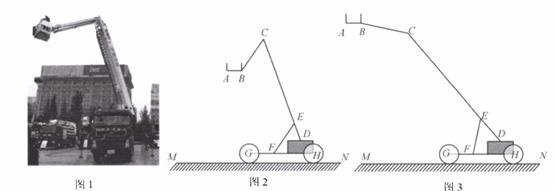
三、解答题（本题有6小题，共46分，解答需写出必要的文字说明或演算步骤）

19. 计算：

(1)、（π-3.14）⁰+（ $\frac{1}{2}$ ）^-1+（-1）²⁰²¹

(2)、（x+1）²-x（x+2）

查看试题解析
20. 解下列方程（组）：

(1)、 ${\begin{cases} x - y = 3 \\ 3 x + 2 y = 4 \end{cases}$

(2)、 $\frac{x + 3}{x - 1} + \frac{x}{1 - x} = 2$

查看试题解析
21. 先化简，再求值： $(2 - \frac{1}{x - 1}) \cdot \frac{x - 1}{x^{2} - 4 x + 4}$ ，请在-1，0，1，2中选一个数代入求值。

查看试题解析
22. 为丰富学生的课余生活，培养学生的爱好，陶冶学生的情操，某校开展学生拓展课，为了解学生各社团活动的参与人数，该校对社团活动进行了抽样调查，制作出如下的统计图。根据该统计图，完成以下问题：

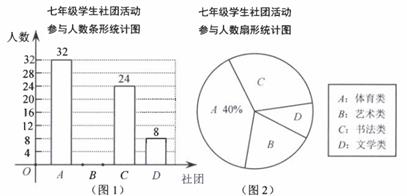(1)、这次共调查了名学生

(2)、请把统计图1补充完整。

(3)、已知该校七年级共有680名学生参加社团活动，请根据样本估算该校七年级学生参加艺术类社团的人数

查看试题解析
23. 如图，AB∥CD，E是CD上一点，AE交BC于点F，且∠ABE=∠DBC，∠ABC=∠AEB。

(1)、试判断AE与BD的位置关系，并说明理由。

(2)、若BE平分∠CBD，∠AEB=40°，求∠D的度数。

查看试题解析
24. 为了庆祝建党100周年，某区在文化广场的一块长方形ABCD的空地上，用花卉摆放“100”字样和四个相同的小正方形（如图），其中AB=7.2米，BC=10.8米，三个数之间摆放的距离与四个小正方形的边长相等．设小正方形的边长为x米，数字的宽度均为y米。

(1)、请用关于x，y的代数式表示“0”内部小长方形的长和宽。

(2)、若“0”内部小长方形的长和宽分别是3.6米和1.4米。
①求x，y的值；

②为了整体美观，将在四个正方形、“100”及“0”的内部小长方形分别摆放甲、乙、丙三种花卉，三种花卉的单价都为整数，其中甲花卉的单价在95~125元/米²之间（含95和125），乙、丙两种花卉的单价之和为300元/米²。已知三种花卉总价为6200元，则丙花卉的单价是元/米²

查看试题解析