浙江省温州市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-07-12 类型：期末考试
一、选择题（本题有10小题，每小题3分，共30分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）
-
1. 如果式子 有意义，那么x的取值范围是（ ）A、x≥2 B、x≤2 C、x>2 D、x<22. 下列四个银行标志中，是中心对称图形的标志是（ ）A、
B、
C、
D、
3. 某校“建党一百周年”演讲比赛中，有9名学生参加决赛，他们的最终成绩各不相同。其中一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（ ）A、众数 B、方差 C、中位数 D、平均数4. 下列选项中的计算，正确的是（ ）A、 =±4 B、3 - =3 C、 =-5 D、5. 如图，为测量BC两地的距离，小明在池塘外取点A，得到线段AB，AC，并取AB，AC的中点D，E，连结DE。测得DE的长为6米，则B，C两地相距（ ）
A、9米 B、10米 C、11米 D、12米6. 用配方法解x2-4x-5=0时，配方结果正确的是（ ）A、（x-2）2=5 B、（x-4）2=5 C、（x-2）2=9 D、（x-2）2=17. 用反证法证明“在△ABC中，若∠A>∠B，则a>b“时，应假设（ ）A、a<b B、a≤b C、a=b D、a≥b8. 为了美化环境，温州市某乡村加大对绿化的投资。2018年用于绿化投资100万元，2020年用于绿化投资144 万元。设这两年绿化投资的年平均增长率为x，根据题意所列方程为（ ）A、100x2=144 B、100（1+x）=144 C、100（1+x）2=144 D、100（1+2x）=1449. 对于反比例函数y= ，当y>2时，x的取值范围是（ ）A、x>-4 B、x<-4 C、-4<x<0 D、x<-4或x>010. 在正方形ABCD的对角线BD上取一点E，连结AE，过点E作EF⊥AE交BC于点F，将线段EF向右平移m个单位，使得点E落在CD上，F落在BC上，已知AE+EF+CF=24，CD=10，则m的值为（ ）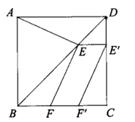
A、6 B、4 -2 C、4 D、2 +2二、填空题（本题有8小题，每小题3分，共24分）
-
11. 在平面直角坐标系中，点（2，3）关于原点对称的点的坐标是。12. 某校八年级（1）班甲、乙两名同学在10次射箭成绩情况如下表所示，体育老师根据这10次成绩，从稳定性角度考虑，会选择同学参加比赛。（填“甲”或“乙”）
平均数（环
众数（环）
中位数（环）
方差 （环）
甲
8.7
9
9
1.5
乙
8.7
10
9
3.2
13. 五边形的内角和等于 度．14. 如图，在矩形ABCD中，AC，BD相交于点O，已知OD=5，AD=6，则该矩形的周长是。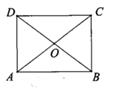
15. 若关于x的方程x2+6x+a=0有两个相等的实数根，则a的值为 。16. 如图，△OAB是等边三角形，点B在x轴的正半轴上，点A在反比例函数y= （x>0）的图象上，则△OAB的面积为 。
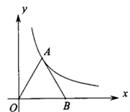17. 如图，在 ABCD中，点E为边BC上一点，连结AE，DE，AE=DE=BE，∠CDE=24°，则∠B=度。
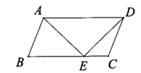18. 图1是一款平衡荡板器材，示意图如图2，A，D为支架顶点，支撑点B，C，E，F在水平地面同一直线上，G，H为荡板上固定的点，GH∥BF，测量得AG=GH=DH，Q为DF上一点且离地面1m，旋转过程中，AG始终与DH保持平行，如图3，当旋转至A，Q，H在同一直线上时，连结G'Q，测得G'Q=1.6m，∠DQG=90°，此时荡板G'H距离地面0.6m，则点D离地面的距离为m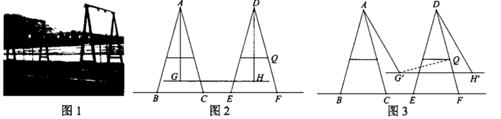
三、解答题（本题有6小题，共46分，解答时需要写出必要的文字说明、演算步骤或证明过程）
-
19.(1)、计算：(2)、解方程：x2+3x=020. 如图，24个全等的正三角形组成的正六边形网格，正三角形的顶点称为格点。
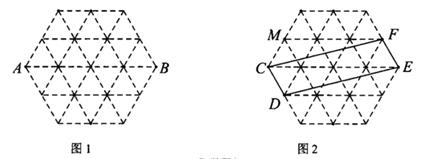(1)、在图1中画出以AB为对角线的格点矩形APBQ（顶点均在格点上）。(2)、如图2，已知点C，D，E，F，M均在格点上，请在网格中（包含边界）找一个格点N，连结MN，使得直线MN平分四边形CDEF的面积。21. 某一家工程咨询公司技术部门员工一月份的工资报表如下总工程师
工程师
工程师助理
技术员
客服
月收入（千元）
21
11
8
7
5
人数 （人）
1
2
4
10
3
(1)、分别求该公司技术部门员工一月份工资的平均数、中位数和众数。(2)、某天，一位员工辞职了，若其他员工的月收入不变，部门的平均收入升高了，你认为辞职的可能是哪个岗位上的员工？并说明理由。22. 经过实验获得两个变量x（x>0），y（y>0）的一组对应值如下表。x
1
2
3
4
5
6
y
6
3
2
1.5
1.2
1
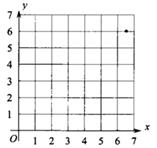(1)、用描点法在右边图中画出函数的图象。(2)、求这个函数的表达式。(3)、当0<a≤x≤2a时，记函数的最大值为M，最小值为N，直接写出 的值。23. 为响应国家“垃圾分类"的号召，温州市开始实施《城镇垃圾分类标准》，某商场向厂家订购了A，B两款垃圾桶共100个。已知购买A款垃圾桶个数不超过30个时，每个A款垃圾桶进价为80元，若超过30个时，每增加1个垃圾桶，进价减少2元，厂家为保障盈利，每个A款垃圾桶进价不低于50元。每个B款垃圾桶的进价为40元，设所购买A款垃圾桶的个数为x个。(1)、根据信息填表：款式
数量（个）
进价（元/个）
A
x（不超过30个时）
80
x （超过30个时）
B
40
(2)、若订购的垃圾桶的总进价为4800元，则该商场订购了多少个A款垃圾桶？24. 如图1，四边形ABCD是平行四边形，点E在边AD上，连结BE，过点D作DF∥BE，交BC于点F，点G，H分别是BE，DF的中点，连结EH，GF。
(1)、求证：四边形EGFH为平行四边形。(2)、若BC=10，AB=6，∠ABC=60°。①当BG=GF时，求四边形EGFH的面积。
②如图2，延长FG交AB于点P，连结AG，记△APG的面积为S1 ， △BPG的面积为S2 ， 若FP⊥AB，求 的值。