江西省吉安市2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-07-09 类型：期末考试

进入出卷网下载

一、单选题

1. 不等式 $- x^{2} + 1 < 0$ 的解集是（）

A、 ${x ∣ x > 1}$ B、 ${x ∣ x > \pm 1}$ C、 ${x | x < - 1$ 或 $x > 1}$ D、 ${x | - 1 < x < 1}$

查看试题解析
2. 某校高一年级有男生450人，女生550人，若在各层中按比例抽取样本，总样本量为40，则在男生、女生中抽取的人数分别为（）

A、17，23 B、18，22 C、19，21 D、22，18

查看试题解析
3. 等差数列 ${a_{n}}$ 前 $n$ 项和为 $S_{n}$ ，若 $a_{1002} + a_{1020} = 2$ ，则 $S_{2021}$ 的值为（）

A、2 B、2020 C、2021 D、2022

查看试题解析
4. 用系统抽样的方法从全校800人中抽取40人做问卷调查，并将他们随机编号为0，1，2，3，…，799，已知第一组中采用抽签法抽到的号码为15，则第三组抽取到的号码是（）

A、25 B、35 C、45 D、55

查看试题解析
5. 下图是把二进制的数1111_（2）化成十进制数的一个程序框图，则判断框内应填入的条件是（）

A、 $i < 3$ B、 $i \leq 3$ C、 $i > 3$ D、 $i > 4$

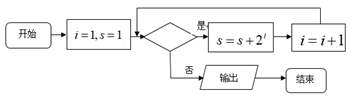查看试题解析
6. 2021年3月的中美高层战略对话中国代表的表现令国人振奋，印有杨洁篪“中国人不吃这一套”金句的 $T$ 恤衫成为热销产品，某商场五天内这种 $T$ 恤衫的销售情况如下表：

第 $x$ 天

1

2

3

4

5

销售量 $y$ （件）

19

39

59

79

104

则下列说法正确的是（）

A、 $y$ 与 $x$ 负相关 B、 $y$ 与 $x$ 正相关 C、 $y$ 与 $x$ 不相关 D、 $y$ 与 $x$ 成正比例关系

查看试题解析
7. 从装有2个白球和3个红球的口袋内任取2个球，那么互斥而不对立的两个事件是（）

A、至少一个白球，都是白球 B、至少有一个白球，至少有一个红球 C、至少一个白球，都是红球 D、恰有一个白球，恰有2个白球

查看试题解析
8. 若 $a > b > 0$ ， $m < 0$ ．则下列不等式成立的是（）

A、 $\frac{a - m}{b - m} > \frac{a}{b}$ B、 $\frac{a - m}{b - m} < \frac{a}{b}$ C、 $\frac{m}{a - b} > 1$ D、 $a m^{2} < b m^{2}$

查看试题解析
9. 设 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边为 $a$ ， $b$ ， $c$ ，则下列命题不正确的是（）

A、 $\sin A > \sin B$ ，则 $A > B$ B、若 $\sin 2 A = \sin 2 B$ ，则 $A = B$ C、若 $A$ ， $B$ ， $C$ 成等差数列，则 $B = \frac{π}{3}$ D、若 $a ： b ： c = 1 ： \sqrt{3} ： 2$ ，则 $C = \frac{π}{2}$

查看试题解析
10. 3.12日为植树节，某单位组织10名职工分成两组开展义务植树活动，以下茎叶图记录了甲、乙两组五名职工的植树棵数．（参考公式：样本数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的方差 $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}]$ ，其中 $\bar{x}$ 为样本平均数），下列说法，正确的是（）

A、甲组植树棵数的平均数不高于乙组植树棵数的平均数 B、甲组植树棵数的众数是9 C、乙组植树棵数的方差 $s^{2} = 2$ D、甲、乙两组中植树棵数的标准差 $s_{甲} > s_{乙}$

查看试题解析
11. 如图，点 $A$ ， $B$ ， $C$ 在半圆 $O$ 上， $A O C D$ 为正方形，在图形中随机取一点，则此点取自阴影部分的概率为（）

A、 $\frac{2}{π}$ B、 $\frac{1}{π + 2}$ C、 $\frac{2}{π + 2}$ D、 $\frac{2}{π + 4}$

查看试题解析
12. 设 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边为 $a$ ， $b$ ， $c$ ，若 $2 a \cos B = b + c$ ，则 ${(\frac{a}{b})}^{2} + \frac{b}{c}$ 的最小值为（）

A、4 B、 $2 \sqrt{3}$ C、3 D、 $2 \sqrt{2}$

查看试题解析

二、填空题

13. 100与2020的最大公因数为．

查看试题解析
14. 秦九韶是我国南宋时期的数学家，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，具有世界意义的重要贡献．如图是实现该算法的程序框图．执行该程序框图，若输入的 $x = 3$ ， $n = 2$ ，依次输入的 $a$ 为2，3，4，则输出的 $s =$ ．

查看试题解析
15. 函数 $y = \sqrt{k x^{2} - 2 k x + 4}$ 的定义域为 $R$ ，则实数 $k$ 的取值范围为．

查看试题解析
16. 一个数列从第二项起，每一项与前一项的和都等于同一个常数，则称此数列为等和数列，这个常数叫做等和数列的公和，设等和数列 ${a_{n}}$ 的公和为3，前 $n$ 项和为 $S_{n}$ ，若 $S_{2021} = 3032$ ，则 $a_{1} =$ ．

查看试题解析

三、解答题

17.

(1)、用掷两枚质地均匀的硬币做胜负游戏，规定：两枚硬币同时出现正面或同时出现反面算甲胜，一个正面、一个反面算乙胜．这个游戏是否公平？请通过计算说明．

(2)、若投掷质地均匀的三枚硬币，规定：三枚硬币同时出现正面或同时出现反面算甲胜，其他情况算乙胜．这个游戏是否公平？请通过计算说明．

查看试题解析
18. 在 $△ A B C$ 中， $a$ 、 $b$ 、 $c$ 分别是角 $A$ 、 $B$ 、 $C$ 的对边， $b \cos A + (2 c + a) \cos B = 0$ ．

(1)、求角 $B$ 的大小；

(2)、若 $b = \sqrt{7}$ ， $△ A B C$ 的周长为 $3 + \sqrt{7}$ ，求 $△ A B C$ 的面积．

查看试题解析
19. 在等比数列 ${a_{n}}$ 中， $a_{2} = 2$ ，且 $a_{2}$ 、 $a_{3} + 1$ 、 $a_{4}$ 成等差数列．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $a_{2}$ 、 $a_{3} + 1$ 、 $a_{4}$ 为等差数列 ${b_{n}}$ 的连续三项，其中 $b_{1} = a_{2}$ ，设数列 ${b_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $S_{n} = 155$ ，求 $n$ 的值．

查看试题解析
20. 为了全面提高学生的体质健康水平，充分发挥体育考试的激励作用，吉安市今年中考体育考试成绩以满分60分计入中招成绩总分，其中1分钟跳绳是选考项目．某校体育组决定从九年级抽取部分学生进行跳绳测试，并将跳绳的次数按 $[60 ， 80)$ 、 $[80 ， 100)$ 、 $[100 ， 120)$ 、 $[120 ， 140)$ 、 $[140 ， 160]$ 分组，得到顺率分布直方图（如图）．已知图中从左到右的前四个小组的频率分别是0.1、0.3、0.4、0.15，第三小组的频数是24．

(1)、求第五小组的频率和参加这次测试的学生人数；

(2)、估计这次测试学生跳绳次数的中位数；

(3)、统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计参加这次测试学生跳绳的平均次数．

查看试题解析
21. 已知数列 ${a_{n}}$ 前 $n$ 项和为 $S_{n}$ ，满足 $S_{n} = (\frac{1}{2} n + q) a_{n}$ （ $q$ 为常数）， $a_{1} = 1$ ．

(1)、判断数列 ${a_{n}}$ 是不是等差或等比数列，并求出数列 ${a_{n}}$ 的通项公式．

(2)、求数列 ${a_{n} + 3^{n - 1}}$ 的前 $n$ 项和 $T_{n}$ ．

查看试题解析
22. 动物园要围成相同面积的矩形虎笼两间，一面利用原有的墙，其他各面用钢筋网围成（如图）．若每间虎笼的面积为 $24 m^{2}$ ，墙长 $a$ 米，则每间虎笼的长、宽各设计为多少时，可使围成西间虚笼的钢筋网总长最小？并求出钢筋网的长度．

查看试题解析

第 $x$ 天	1	2	3	4	5
销售量 $y$ （件）	19	39	59	79	104