2021年高考数学真题分类汇编专题09:三角函数与解三角形
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1. 在 中,已知 ,则 ( )A、1 B、 C、 D、32. 若 , ,则 ( )A、 B、 C、 D、3. 2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.右图是三角高程测量法的一个示意图,现有以A,B,C三点,且A,B,C在同一水平而上的投影A’,B’,C'满足 .由c点测得B点的仰角为15°,曲, 与 的差为100 :由B点测得A点的仰角为45°,则A,C两点到水平面 的高度差 约为( )
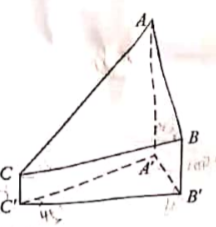 A、346 B、373 C、446 D、4734. 函数f(x)=sin +cos 的最小正周期和最大值分别是( )A、3 和 B、3 和2 C、 和 D、 和25. ( )A、 B、 C、 D、6. 把函数y=f(x)图象上所有点的横坐标缩短到原来的 倍,纵坐标不变,再把所得曲线向右平移 个单位长度,得到函数y=sin(x- )的图像,则f(x)=( )A、sin( ) B、sin( ) C、sin( ) D、sin( )7. 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高。如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”。则海岛的高AB=( ).
A、346 B、373 C、446 D、4734. 函数f(x)=sin +cos 的最小正周期和最大值分别是( )A、3 和 B、3 和2 C、 和 D、 和25. ( )A、 B、 C、 D、6. 把函数y=f(x)图象上所有点的横坐标缩短到原来的 倍,纵坐标不变,再把所得曲线向右平移 个单位长度,得到函数y=sin(x- )的图像,则f(x)=( )A、sin( ) B、sin( ) C、sin( ) D、sin( )7. 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高。如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”。则海岛的高AB=( ). A、 B、 C、 D、8. 下列区间中,函数f(x)=7sin( )单调递增的区间是( )A、(0, ) B、( , ) C、( , ) D、( , )9. 若tan =-2,则 =( )A、 B、 C、 D、10. 已知 是互不相同的锐角,则在 三个值中,大于 的个数的最大值是( )A、0 B、1 C、2 D、3
A、 B、 C、 D、8. 下列区间中,函数f(x)=7sin( )单调递增的区间是( )A、(0, ) B、( , ) C、( , ) D、( , )9. 若tan =-2,则 =( )A、 B、 C、 D、10. 已知 是互不相同的锐角,则在 三个值中,大于 的个数的最大值是( )A、0 B、1 C、2 D、3二、多选题
-
11. 下图是函数y= sin(ωx+φ)的部分图像,则sin(ωx+φ)= ( )
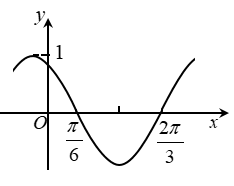
A、 B、 C、 D、三、填空题
-
12. 已知函数 的部分图像如图所示,则 = .
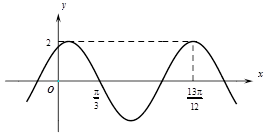 13. 已知函数 的部分图像如图所示,则满足条件 的最小正整数x为。
13. 已知函数 的部分图像如图所示,则满足条件 的最小正整数x为。 14. 记△ABC的内角A,B,C的对边分别为a,b,c,面积为 ,B=60°,a2+c2=3ac,则b=.15. 若点 与点 关于 轴对称,写出一个符合题意的 .16. 我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,记大正方形的面积为 ,小正方形的面积为 ,则 .
14. 记△ABC的内角A,B,C的对边分别为a,b,c,面积为 ,B=60°,a2+c2=3ac,则b=.15. 若点 与点 关于 轴对称,写出一个符合题意的 .16. 我国古代数学家赵爽用弦图给出了勾股定理的证明.弦图是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形(如图所示).若直角三角形直角边的长分别是3,4,记大正方形的面积为 ,小正方形的面积为 ,则 .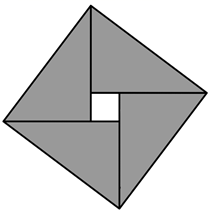 17. 在 中, ,M是 的中点, ,则 , .
17. 在 中, ,M是 的中点, ,则 , .四、解答题
-
18. 记△ABC的内角A,B,C的对边分别为a.,b.,c,已知 =ac,点D在边AC 上,BDsin∠ABC=asinC.(1)、证明:BD = b:(2)、若AD = 2DC .求cos∠ABC.19. 在 中,角A,B,C所对的边长分别为 .(1)、若 ,求 的面积;(2)、是否存在正整数a,使得 为钝角三角形?若存在,求出a的值;若不存在,说明理由.
-