全国历年中考数学真题精选汇编：数据收集、整理与分析
试卷更新日期：2021-07-09 类型：二轮复习
一、单选题
-
1. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋，设货架上原有鸡蛋的质量（单位：g）平均数和方差分别为 ，s2 ， 该顾客选购的鸡蛋的质量平均数和方差 ，s12 ， 则下列结论一定成立的是（ ）A、 ＜ B、 ＞ C、s2＞s12 D、s2＜s122. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人，则初中生有（ ）
某天参观温州数学名人馆的学生人数统计图
A、45人 B、75人 C、120人 D、300人3. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 （单位：环）及方差 （单位：环 ）如下表所示：甲
乙
丙
丁
9
8
9
9
1.6
0.8
3
0.8
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（ ）
A、甲 B、乙 C、丙 D、丁4. 5月1日至7日，我市每日最高气温如图所示，则下列说法错误的是（ ）
A、中位数是33℃ B、众数是33℃ C、平均数是 ℃ D、4日至5日最高气温下降幅度较大5. 在一次心理健康教育活动中，张老师随机抽取了40名学生进行了心理健康测试，并将测试结果按“健康、亚健康、不健康”绘制成下列表格，其中测试结果为“健康”的频率是（ ）.类型
健康
亚健康
不健康
数据（人）
32
7
1
A、32 B、7 C、 D、6. 甲、乙两人进行飞镖比赛，每人各投6次，他们的成绩如下表（单位：环）：甲
6，7，8，8，9，9
乙
5，6，x，9，9，10
如果两人的比赛成绩的中位数相同，那么乙的第三次成绩x是（ ）
A、6环 B、7环 C、8环 D、9环7. 在2021年初中毕业生体育测试中，某校随机抽取了10名男生的引体向上成绩，将这组数据整理后制成如下统计表：成绩（次）
12
11
10
9
人数（名）
1
3
4
2
关于这组数据的结论错误的是（ ）
A、中位数是10.5 B、平均数是10.3 C、众数是10 D、方差是0.818. 小明调查了本班每位同学最喜欢的颜色，并绘制了不完整的扇形图1及条形图2（柱的高度从高到低排列）．条形图不小心被撕了一块，图2中 “（ ）”应填的颜色是（ ）
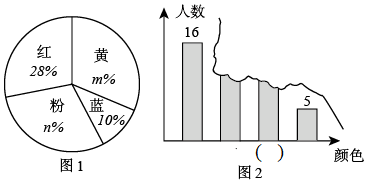A、蓝 B、粉 C、黄 D、红9. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，则所调查学生睡眠时间的众数，中位数分别为（ ）
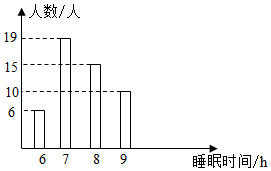A、7h ， 7h B、8h ， 7.5h C、7h ， 7.5h D、8h ， 8h10. 根据下表中的信息解决问题：数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（ ）
A、3个 B、4个 C、5个 D、6个11.为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m3），绘制了统计图．如图所示，下面四个推断（ ）
①年用水量不超过180m3的该市居民家庭按第一档水价交费；
②年用水量超过240m3的该市居民家庭按第三档水价交费；
③该市居民家庭年用水量的中位数在150﹣180之间；
④该市居民家庭年用水量的平均数不超过180．
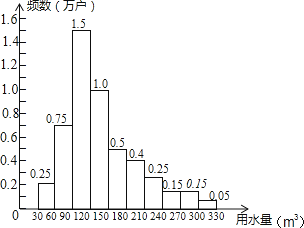A、①③ B、①④ C、②③ D、②④二、填空题
-
12. 为庆祝建党100周年，某校举行“庆百年红歌大赛”.七年级5个班得分分别为85，90，88，95，92，则5个班得分的中位数为分.13. 某学校组织了主题为“保护湘江，爱护家园”的手抄报作品征集活动.先从中随机抽取了部分作品，按 ， ， ， 四个等级进行评价，然后根据统计结果绘制了如下两幅不完整的统计图.那么，此次抽取的作品中，等级为 等的作品份数为.
14. 已知一组数据：a、4、5、6、7的平均数为5，则这组数据的中位数是.15. 开学前，根据学校防疫要求，小芸同学连续14天进行了体温测量，结果统计如下表：体温（ ）
36.3
36.4
36.5
36.6
36.7
36.8
天数（天）
2
3
3
4
1
1
这14天中，小芸体温的众数是 .
16. 一组数据2，1，3，1，2，4的中位数是.17. 现有甲、乙两种糖果的单价与千克数如下表所示甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果盒3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克
18. 如图是根据甲、乙两人5次射击的成绩（环数）制作的折线统计图.你认为谁的成绩较为稳？（填“甲”或“乙”）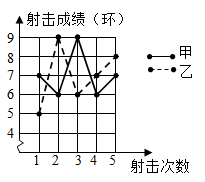
19. 某中学规定学生的学期体育成绩满分为100，其中体育课外活动占30%，期末考试成绩占70%，小彤的这两项成绩依次是90，80.则小彤这学期的体育成绩是.三、综合题
-
20. 某机构为了解宿迁市人口年龄结构情况，对宿迁市的人口数据进行随机抽样分析，绘制了如下尚不完整的统计图表：
类别
A
B
C
D
年龄（t岁）
0≤t<15
15≤t<60
60≤t<65
t≥65
人数（万人）
4.7
11.6
m
2.7
根据以上信息解答下列问题：
(1)、本次抽样调查，共调查了万人；(2)、请计算统计表中m的值以及扇形统计图中“C”对应的圆心角度数；(3)、宿迁市现有人口约500万人，请根据此次抽查结果，试估计宿迁市现有60岁及以上的人口数量.21. 高尔基说：“书，是人类进步的阶梯.”阅读可以启智增慧，拓展视野，……为了解学生寒假阅读情况.开学初学校进行了问卷调查，并对部分学生假期（24天）的阅读总时间作了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为t（小时），阅读总时间分为四个类别： ， ， ， ，将分类结果制成如下两幅统计图（尚不完整）.
根据以上信息，回答下列问题：
(1)、本次抽样的样本容量为；(2)、补全条形统计图；(3)、扇形统计图中a的值为 ， 圆心角 的度数为；(4)、若该校有2000名学生，估计寒假阅读的总时间少于24小时的学生有多少名？对这些学生用一句话提一条阅读方面的建议.22. 为进一步做好“光盘行动”，某校食堂推出“半份菜”服务，在试行阶段，食堂对师生满意度进行抽样调查.并将结果绘制成如下统计图（不完整）.
(1)、求被调查的师生人数，并补全条形统计图，(2)、求扇形统计图中表示“满意”的扇形圆心角度数.(3)、若该校共有师生1800名，根据抽样结果，试估计该校对食堂“半份菜”服务“很满意”或“满意”的师生总人数.23. 某市在实施居民用水定额管理前，对居民生活用水情况进行了调查，通过简单随机抽样，获得了100个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如下表：序号
1
2
…
25
26
…
50
51
…
75
76
…
99
100
月均用水量/t
1.3
1.3
…
4.5
4.5
…
6.4
6.8
…
11
13
…
25.6
28
(1)、求这组数据的中位数.已知这组数据的平均数为 ，你对它与中位数的差异有什么看法？(2)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使75%的家庭水费支出不受影响，你觉得这个标准应该定为多少？24. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：平均数
中位数
众数
方差
甲
175
93.75
乙
175
175
180，175，170
(1)、求 、 的值；(2)、若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；(3)、根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.25. 今年9月，第十四届全国运动会将在陕西省举行本届全运会主场馆在西安，开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温，从中随机抽取了60天的日平均气温，并绘制成如下统计图：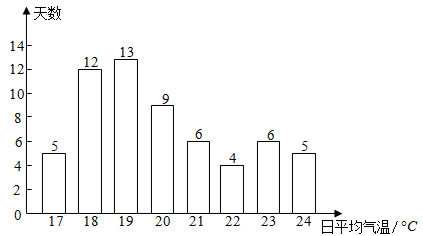
根据以上信息，回答下列问题：
(1)、这60天的日平均气温的中位数为 ， 众数为；(2)、求这60天的日平均气温的平均数；(3)、若日平均气温在18℃~21℃的范围内（包含18℃和21℃）为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.26. 某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程.为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查.并根据调查结果绘制成如图所示的条形统计图和扇形统计图（部分信息未给出）.
请你根据以上信息解决下列问题：(1)、参加问卷调查的学生人数为 ▲ 名.补全条形统计图（画图并标注相应数据）；(2)、在扇形统计图中，选择“陶艺”课程的学生占%；(3)、若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？27. 国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出，要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法，抽取了八年级部分学生，对他们一周内平均每天的睡眠时间 （单位： ）进行了调查，将数据整理后得到下列不完整的统计图表：组别
睡眠时间分组
频数
频率
4
0.08
8
0.16
10
21
0.42
0.14
请根据图表信息回答下列问题：
(1)、频数分布表中， ， ；(2)、扇形统计图中， 组所在扇形的圆心角的度数是 ；(3)、请估算该校600名八年级学生中睡眠不足7小时的人数；(4)、研究表明，初中生每天睡眠时长低于7小时，会严重影响学习效率.请你根据以上调查统计结果，向学校提出一条合理化的建议.28. 杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失.为此，市农科所开展了用防雨布保护杨梅果实的实验研究.在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）.在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成如下统计图表（数据分组包含左端值不包含右端值）.甲组杨梅树落果率频数分布表
落果率
组中值
频数（棵）
0≤x＜10%
5%
12
10%≤x＜20%
15%
4
20%≤x＜30%
25%
2
30%≤x＜40%
35%
1
40%≤x＜50%
45%
1
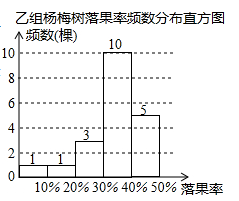(1)、甲、乙两组分别有几棵杨梅树的落果率低于20%？(2)、请用落果率的中位数或平均数，评价市农科所“用防雨布保护杨梅果实”的实际效果；(3)、若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据.29. 为了解某校某年级学生一分钟跳绳情况，对该年级全部360名学生进行一分钟跳绳次数的测试，并把测得数据分成四组，绘制成如图所示的频数表和未完成的频数直方图（每一组不含前一个边界值，含后一个边界值）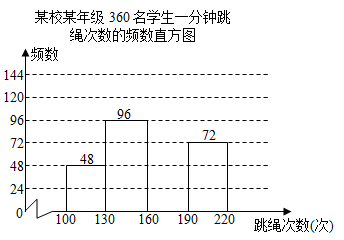
某校某年级360名学生一分钟跳绳次数的频数表
组别（次）
频数
100~130
48
130~160
96
160~190
a
190~220
72
(1)、求 的值；(2)、把频数直方图补充完整；(3)、求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比。30. 某校将学生体质健康测试成绩分为 ， ， ， 四个等级，依次记为4分，3分，2分，1分.为了解学生整体体质健康状况，拟抽样进行统计分析.(1)、以下是两位同学关于抽样方案的对话：小红：“我想随机柚取七年级男、女生各60人的成绩.”
小明：“我想随机柚取七、八、九年级男生各40人的成绩.”
根据右侧学校信息，请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩，请给出抽样方案.
学校共有七、八、九三个年级学生近千人，各段人数相近，每段男、女生人数相当，
.....
(2)、现将随机抽取的测试成绩整理并绘制成如下统计图，请求出这组数据的平均数、中位数和众数.某校部分学生体质健康测试成绩统计图
31. 绍兴莲花落，又称“莲花乐”，“莲花闹”，是绍兴一带的曲艺.为了解学生对该曲种的熟悉度，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成如下不完整的统计图.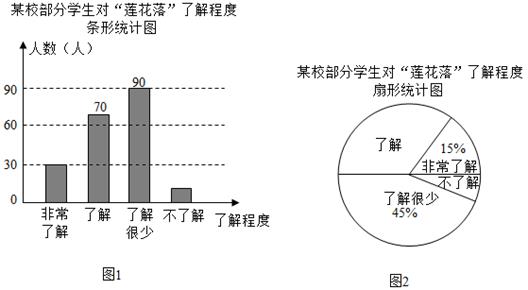
根据图中信息，解答下列问题：
(1)、本次接受问卷调查的学生有多少人？并求图2中“了解”的扇形圆心角的度数.(2)、全校共有1200名学生，请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人.32. 图1表示的是某书店今年1～5月的各月营业总额的情况，图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1～5月的营业总额一共是182万元，观察图1、图2，解答下列向题：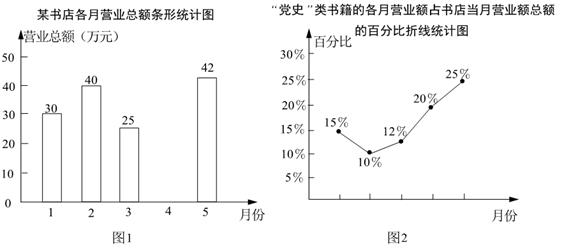
(1)、求该书店4月份的营业总额，并补全条形统计图.(2)、求5月份“党史”类书籍的营业额.(3)、请你判断这5个月中哪个月“党史”类书籍的营业额最高，并说明理由.33. 小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如下测试成绩折线统计图.根据图中信息，解答下列问题：
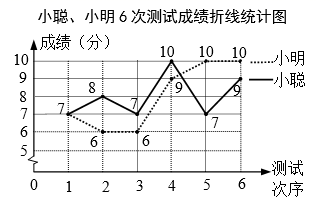(1)、要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 （单位：平方分）.根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由.34. 为推进扬州市“青少年茁壮成长工程”，某校开展“每日健身操”活动，为了解学生对“每日健身操”活动的喜欢程度，随机抽取了部分学生进行调查，将调查信息结果绘制成如下尚不完整的统计图表：抽样调查各类喜欢程度人数分布扇形统计图
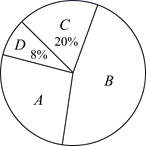
A.非常喜欢 B.比较喜欢 C.无所谓 D.不喜欢
抽样调查各类喜欢程度人数统计表
喜欢程度
人数
A.非常喜欢
50人
B.比较喜欢
m人
C.无所谓
n人
D.不喜欢
16人
根据以上信息，回答下列问题：
(1)、本次调查的样本容量是；(2)、扇形统计图中表示A程度的扇形圆心角为 ，统计表中 ；(3)、根据抽样调查的结果，请你估计该校2000名学生中大约有多少名学生喜欢“每日健身操”活动（包含非常喜欢和比较喜欢）.35. 为庆祝中国共产党建党100周年，某校开展了以“学习百年党史，汇聚团结伟力”为主题的知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分成 五个等级，并绘制了如下不完整的统计图.请结合统计图，解答下列问题：等级
成绩
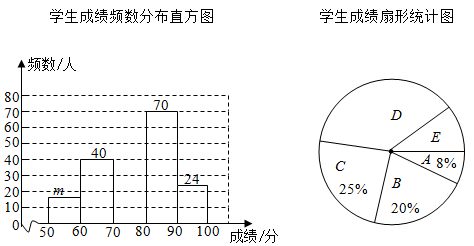(1)、本次调查一共随机抽取了名学生的成绩，频数分布直方图中 ；(2)、补全学生成绩频数分布直方图；(3)、所抽取学生成绩的中位数落在等级；(4)、若成绩在80分及以上为优秀，全校共有2000名学生，估计成绩优秀的学生有多少人?36. 端午节吃粽子是中华民族的传统习俗.某食品厂为了解市民对去年销量较好的A、B、C、D四种粽子的喜爱情况，在端午节前对某小区居民进行抽样调查（每人只选一种粽子），并将调查情况绘制成如下两幅尚不完整的统计图.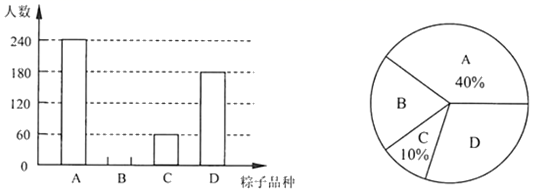
根据以上信息，解答下列问题：
(1)、补全条形统计图；(2)、扇形统计图中，D种粽子所在扇形的圆心角是 ；(3)、这个小区有2500人，请你估计爱吃B种粽子的人数为.37. 某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2021年初的视力数据，并调取该批学生2020年初的视力数据，制成如下统计图（不完整）：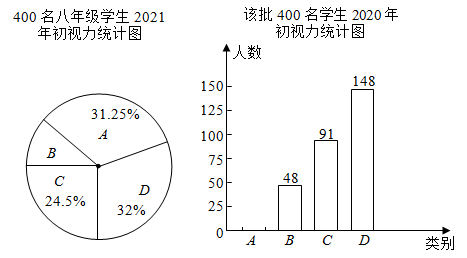
青少年视力健康标准
类别
视力
健康状况
A
视力≥5.0
视力正常
B
4.9
轻度视力不良
C
4.6≤视力≤4.8
中度视力不良
D
视力≤4.5
重度视力不良
根据以上信息，请解答：
(1)、分别求出被抽查的400名学生2021年初轻度视力不良（类别B）的扇形圆心角度数和2020年初视力正常（类别A）的人数．(2)、若2021年初该市有八年级学生2万人，请估计这些学生2021年初视力正常的人数比2020年初增加了多少人？(3)、国家卫健委要求，全国初中生视力不良率控制在69%以内．请估计该市八年级学生2021年初视力不良率是否符合要求？并说明理由．38. 红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查，从试验田中随机抽取了30株，得到的数据如下（单位：颗）：182
195
201
179
208
204
186
192
210
204
175
193
200
203
188
197
212
207
185
206
188
186
198
202
221
199
219
208
187
224
(1)、对抽取的30株水稻稻穗谷粒数进行统计分析，请补全下表中空格，并完善直方图：
谷粒颗数
175≤x＜185
185≤x＜195
195≤x＜205
205≤x＜215
215≤x＜225
频数
8
10
3
对应扇形图中区域
D
E
C
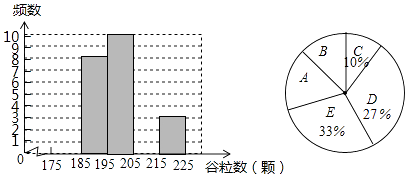
如图所示的扇形统计图中，扇形A对应的圆心角为 度，扇形B对应的圆心角为 度；
(2)、该试验田中大约有3000株水稻，据此估计，其中稻穗谷粒数大于或等于205颗的水稻有多少株？39.某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽查部分学生做了一次问卷调查，要求学生选出自己最喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：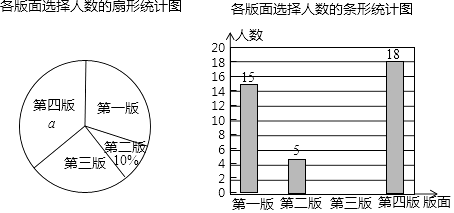
请根据图中信息，解答下列问题：
(1)、该调查的样本容量为 ， a=%，“第一版”对应扇形的圆心角为°；(2)、请你补全条形统计图；(3)、若该校有1000名学生，请你估计全校学生中最喜欢“第三版”的人数．40. 为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：选择意向
所占百分比
文学鉴赏
a
科学实验
35%
音乐舞蹈
b
手工编织
10%
其他
c
根据统计图表中的信息，解答下列问题：
(1)、求本次调查的学生总人数及a，b，c的值；(2)、将条形统计图补充完整；(3)、若该校共有1200名学生，试估计全校选择“科学实验”社团的学生人数．