全国历年中考数学真题精选汇编:锐角三角函数1
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1. 如图, 底边 上的高为 , 底边 上的高为 ,则有( )
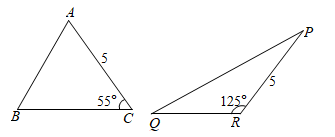 A、 B、 C、 D、以上都有可能2. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )
A、 B、 C、 D、以上都有可能2. 如图,小明利用一个锐角是 的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离 为 , 为 (即小明的眼睛与地面的距离),那么旗杆的高度是( )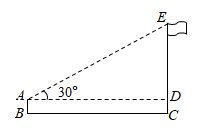 A、 B、 C、 D、3. 如图, 内接于 是 的直径,若 ,则 ( )
A、 B、 C、 D、3. 如图, 内接于 是 的直径,若 ,则 ( )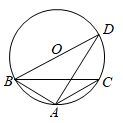 A、 B、 C、3 D、44. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )
A、 B、 C、3 D、44. 如图是一架人字梯,已知 米,AC与地面BC的夹角为 ,则两梯脚之间的距离BC为( )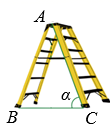 A、 米 B、 米 C、 米 D、 米5. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )
A、 米 B、 米 C、 米 D、 米5. 如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为 ,坡顶D到BC的垂直距离 米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(参考数据: ; ; )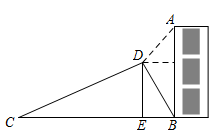 A、69.2米 B、73.1米 C、80.0米 D、85.7米6. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为 ,∠CDF=15°, 则阴影部分的面积为( )
A、69.2米 B、73.1米 C、80.0米 D、85.7米6. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为 ,∠CDF=15°, 则阴影部分的面积为( ) A、 B、 C、 D、7. 如图,直线 与反比例函数 的图象相交于A、B两点,线段 的中点为点C,过点C作x轴的垂线,垂足为点D.直线 过原点O和点C.若直线 上存在点 ,满足 ,则 的值为( )
A、 B、 C、 D、7. 如图,直线 与反比例函数 的图象相交于A、B两点,线段 的中点为点C,过点C作x轴的垂线,垂足为点D.直线 过原点O和点C.若直线 上存在点 ,满足 ,则 的值为( )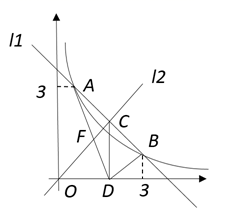 A、 B、3或 C、 或 D、38. 如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即 米,在点E处看点D的仰角为64°,则 的长用三角函数表示为( )
A、 B、3或 C、 或 D、38. 如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即 米,在点E处看点D的仰角为64°,则 的长用三角函数表示为( )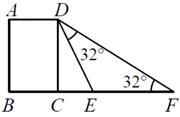 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
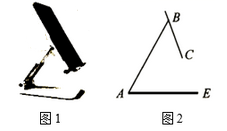 10. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.
10. 将一副三角板如图放置在平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且 ,点E在AD上, ,将这副三角板整体向右平移个单位,C,E两点同时落在反比例函数 的图象上.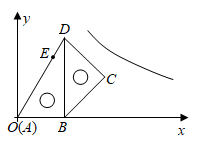 11. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是.
11. 如图,在菱形 中, ,对角线 、 相交于点 ,点 在线段 上,且 ,点 为线段 上的一个动点,则 的最小值是. 12. 图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若 ,则BC长为cm(结果保留根号).
12. 图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若 ,则BC长为cm(结果保留根号).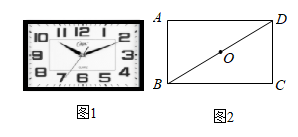 13. 如图是某商场营业大厅自动扶梯示意图.自动扶梯 的倾斜角为 ,在自动扶梯下方地面 处测得扶梯顶端 的仰角为 , 、 之间的距离为4 . 则自动扶梯的垂直高度 = .(结果保留根号)
13. 如图是某商场营业大厅自动扶梯示意图.自动扶梯 的倾斜角为 ,在自动扶梯下方地面 处测得扶梯顶端 的仰角为 , 、 之间的距离为4 . 则自动扶梯的垂直高度 = .(结果保留根号)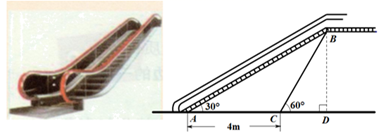
三、计算题
-
14.(1)、计算: .(2)、解不等式: .15. 计算或化简:(1)、 ;(2)、 .16. 计算: .17.(1)、计算:2﹣1+ ﹣sin30°;
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
(2)、化简并求值:1﹣ ,其中a=﹣ .18. 计算:19.(1)、计算: .(2)、先化简,再求值: ,其中 满足 .20.(1)、计算: .(2)、先化简,再求值: ,其中 .四、解答题
-
21. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: 1.414, =1.732).
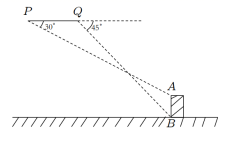 22. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )
22. 2021年,州河边新建成了一座美丽的大桥.某学校数学兴趣小组组织了一次测桥墩高度的活动,如图,桥墩刚好在坡角为 的河床斜坡边,斜坡 长为48米,在点 处测得桥墩最高点 的仰角为 , 平行于水平线 , 长为 米,求桥墩 的高(结果保留1位小数).( , , , )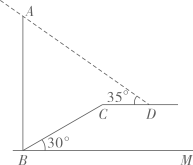
 23. 如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得 , , , , ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)
23. 如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得 , , , , ,设A,B,C,D在同一平面内,求A,B两点之间的距离.(参考数据: .)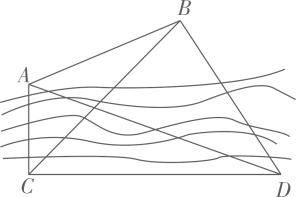 24. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )
24. 乡村振兴使人民有更舒适的居住条件,更优美的生活环境,如图是怡佳新村中的两栋居民楼,小明在甲居民楼的楼顶 处观测乙居民楼楼底 处的俯角是 ,观测乙居民楼楼顶 处的仰角为 ,已知甲居民楼的高为 ,求乙居民楼的高.(参考数据: , ,结果精确到 )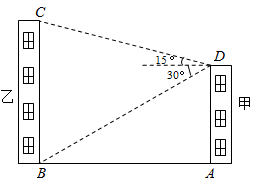 25. “眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )
25. “眉山水街”走红网络,成为全国各地不少游客新的打卡地!游客小何用无人机对该地一标志建筑物进行拍摄和观测,如图,无人机从 处测得该建筑物顶端 的俯角为24°,继续向该建筑物方向水平飞行20米到达 处,测得顶端 的俯角为45°,已知无人机的飞行高度为60米,则这栋建筑物的高度是多少米?(精确到0.1米,参考数据: , , )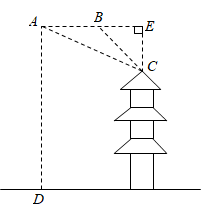 26. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , )
26. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , ) 27. 图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED=48°,BE=110cm,DE=80cm,求活动杆端点D离地面的高度DF.(结果精确到1cm,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
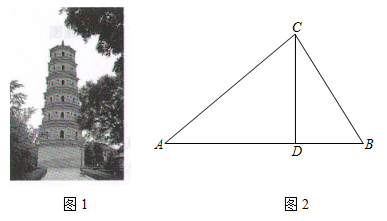
27. 图1是放置在水平地面上的落地式话筒架实物图,图2是其示意图.支撑杆AB垂直于地面l,活动杆CD固定在支撑杆上的点E处.若∠AED=48°,BE=110cm,DE=80cm,求活动杆端点D离地面的高度DF.(结果精确到1cm,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)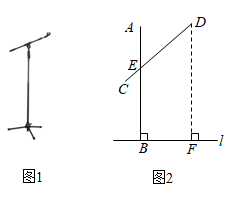 28. 如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
28. 如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:方案设计:如图2,宝塔 垂直于地面,在地面上选取 两处分别测得 和 的度数( 在同一条直线上).
数据收集:通过实地测量:地面上 两点的距离为 .
问题解决:求宝塔 的高度(结果保留一位小数).
参考数据: , .
根据上述方案及数据,请你完成求解过程.
 29. 某天,北海舰队在中国南海例行训练,位于 处的济南舰突然发现北偏西 方向上的 处有一可疑舰艇,济南舰马上通知位于正东方向200海里 处的西安舰,西安舰测得 处位于其北偏西 方向上,请问此时两舰距 处的距离分别是多少?
29. 某天,北海舰队在中国南海例行训练,位于 处的济南舰突然发现北偏西 方向上的 处有一可疑舰艇,济南舰马上通知位于正东方向200海里 处的西安舰,西安舰测得 处位于其北偏西 方向上,请问此时两舰距 处的距离分别是多少?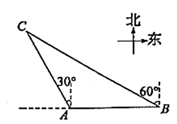
五、综合题
-
30. 如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为 ,测得小区楼房 顶端点C处的俯角为 .已知操控者A和小区楼房 之间的距离为45米,小区楼房 的高度为 米.
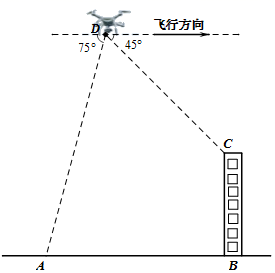 (1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , .计算结果保留根号)31. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
(1)、求此时无人机的高度;(2)、在(1)条件下,若无人机保持现有高度沿平行于 的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据: , .计算结果保留根号)31. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.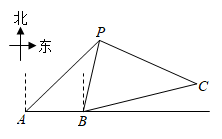 (1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)32. 如图,在四边形 中,对角线 与 交于点O,已知 , ,过点O作 ,分别交 、 于点E,F,连接 , .
(1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)32. 如图,在四边形 中,对角线 与 交于点O,已知 , ,过点O作 ,分别交 、 于点E,F,连接 , .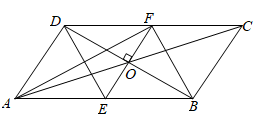 (1)、求证:四边形 是菱形:(2)、设 , , ,求 的长.33. 在几何体表面上,蚂蚁怎样爬行路径最短?
(1)、求证:四边形 是菱形:(2)、设 , , ,求 的长.33. 在几何体表面上,蚂蚁怎样爬行路径最短?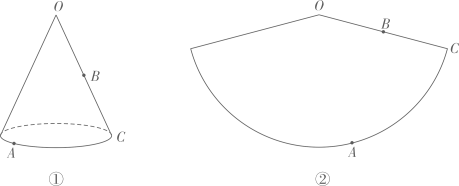
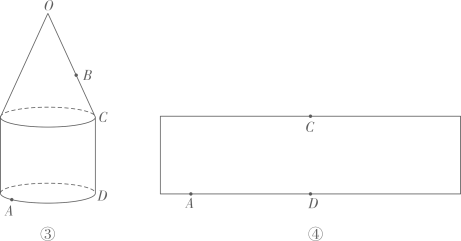 (1)、如图①,圆锥的母线长为 ,B为母线 的中点,点A在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).(2)、图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.
(1)、如图①,圆锥的母线长为 ,B为母线 的中点,点A在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径,并标出它的长(结果保留根号).(2)、图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点,点A在圆柱的底面圆周上.设圆锥的母线长为l,圆柱的高为h.①蚂蚁从点A爬行到点O的最短路径的长为 ▲ (用含l,h的代数式表示).
②设 的长为a,点B在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点A爬行到点B的最短路径的示意图,并写出求最短路径的长的思路.
34. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥,如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:从山顶 处测得河岸 和对岸 的俯角分别为 , .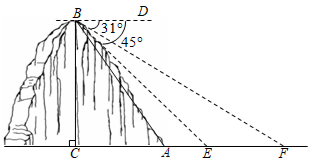
(参考数据: , , )
(1)、求山脚 到河岸 的距离;(2)、若在此处建桥,试求河宽 的长度.(结果精确到 )35. 如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 . (1)、求证:四边形 是平行四边形.(2)、当 , , 时,求 的长.36. 拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内,
(1)、求证:四边形 是平行四边形.(2)、当 , , 时,求 的长.36. 拓展小组研制的智能操作机器人,如图1,水平操作台为l,底座AB固定,高AB为50cm,连杆BC长度为70cm,手臂CD长度为60cm.点B,C是转动点,且AB,BC与CD始终在同一平面内,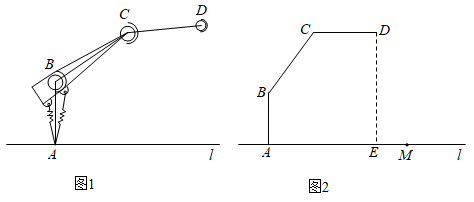 (1)、转动连杆BC,手臂CD,使 , ,如图2,求手臂端点D离操作台 的高度DE的长(精确到1cm,参考数据: , ).(2)、物品在操作台 上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.37. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开.
(1)、转动连杆BC,手臂CD,使 , ,如图2,求手臂端点D离操作台 的高度DE的长(精确到1cm,参考数据: , ).(2)、物品在操作台 上,距离底座A端110cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.37. 我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄 始终平分同一平面内两条伞骨所成的角 ,且 ,从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点 的位置,且A,B, 三点共线, ,B为 中点,当 时,伞完全张开. (1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )38. 已知:如图,矩形 的对角线 相交于点O, .
(1)、求 的长.(2)、当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数据: )38. 已知:如图,矩形 的对角线 相交于点O, .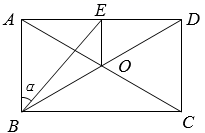 (1)、求矩形对角线的长.(2)、过O作 于点E,连结BE.记 ,求 的值.39. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .
(1)、求矩形对角线的长.(2)、过O作 于点E,连结BE.记 ,求 的值.39. 我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿 摆成如图1所示.已知 ,鱼竿尾端A离岸边 ,即 .海面与地面 平行且相距 ,即 .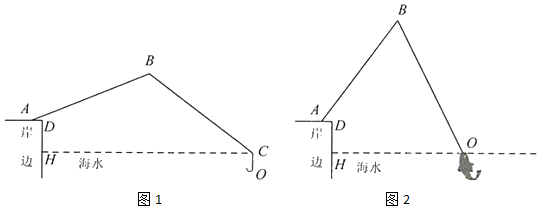 (1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )40. 小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向, C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)、如图1,在无鱼上钩时,海面上方的鱼线 与海面 的夹角 ,海面下方的鱼线 与海面 垂直,鱼竿 与地面 的夹角 .求点O到岸边 的距离;(2)、如图2,在有鱼上钩时,鱼竿与地面的夹角 ,此时鱼线被拉直,鱼线 ,点O恰好位于海面.求点O到岸边 的距离.(参考数据: , , , , , )40. 小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向, C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.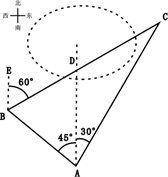 (1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).
(1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).