全国历年中考数学真题精选汇编:图形变换与视图1
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1. 在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到 ,第二次旋转后得到 ,…,依次类推,则点 的坐标为( )
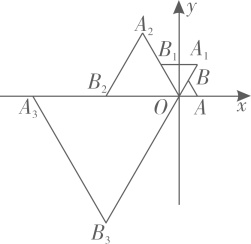 A、 B、 C、 D、2. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )
A、 B、 C、 D、2. 如图,反比例函数 的图象经过点 ,过A作 轴于点B,连 ,直线 ,交x轴于点C,交y轴于点D,若点B关于直线 的对称点 恰好落在该反比例函数图象上,则D点纵坐标为( )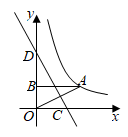 A、 B、 C、 D、3. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( )
A、 B、 C、 D、3. 如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是( ) A、 B、 C、 D、4. 如图,在以 为直径的 中,点 为圆上的一点, ,弦 于点 ,弦 交 于点 ,交 于点 .若点 是 的中点,则 的度数为( )
A、 B、 C、 D、4. 如图,在以 为直径的 中,点 为圆上的一点, ,弦 于点 ,弦 交 于点 ,交 于点 .若点 是 的中点,则 的度数为( )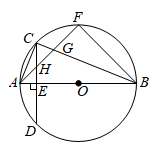 A、18° B、21° C、22.5° D、30°5. 我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )
A、18° B、21° C、22.5° D、30°5. 我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )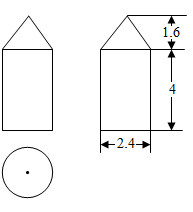 A、 B、 C、 D、6. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( )
A、 B、 C、 D、6. 如图,将 绕点 逆时针旋转 得到 ,若 且 于点 ,则 的度数为( ) A、 B、 C、 D、7. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )
A、 B、 C、 D、7. 如图,图形甲与图形乙是位似图形, 是位似中心,位似比为 ,点 , 的对应点分别为点 , .若 ,则 的长为( )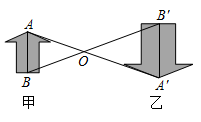 A、8 B、9 C、10 D、158. 如图,树AB在路灯O的照射下形成投影AC,已知路灯高 ,树影 ,树AB与路灯O的水平距离 ,则树的高度AB长是( )
A、8 B、9 C、10 D、158. 如图,树AB在路灯O的照射下形成投影AC,已知路灯高 ,树影 ,树AB与路灯O的水平距离 ,则树的高度AB长是( )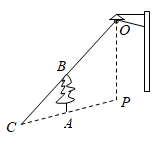 A、 B、 C、 D、9. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )
A、 B、 C、 D、9. 如图, 中, , 、 相交于点D, , , ,则 的面积是( )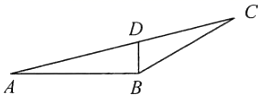 A、 B、 C、 D、10. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
A、 B、 C、 D、10. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )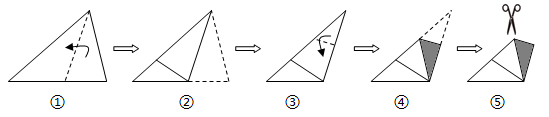 A、等腰三角形 B、直角三角形 C、矩形 D、菱形11. 在正方形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )
A、等腰三角形 B、直角三角形 C、矩形 D、菱形11. 在正方形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得 ,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,下列正确的是( )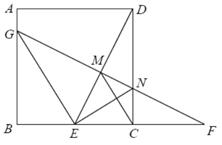
① ; ② ; ③ ; ④ .
A、4 B、3 C、2 D、1二、填空题
-
12. 如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CF=2AF,BE交AD于点F,则△AFE面积的最大值是.
 13. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.
13. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.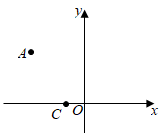 14. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.
14. 如图,将 绕点A逆时针旋转到 的位置,使点 落在 上, 与 交于点E,若 ,则 的长为.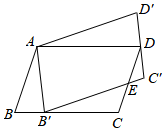 15. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.
15. 如图,将三角形纸片 折叠,使点 、 都与点 重合,折痕分别为 、 .已知 , , ,则 的长为.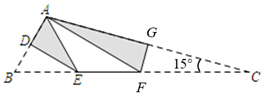 16. 如图,射线 、 互相垂直, ,点 位于射线 的上方,且在线段 的垂直平分线 上,连接 , .将线段 绕点 按逆时针方向旋转得到对应线段 ,若点 恰好落在射线 上,则点 到射线 的距离 .
16. 如图,射线 、 互相垂直, ,点 位于射线 的上方,且在线段 的垂直平分线 上,连接 , .将线段 绕点 按逆时针方向旋转得到对应线段 ,若点 恰好落在射线 上,则点 到射线 的距离 .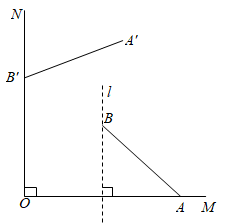 17. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
17. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=. 18. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。
18. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。 19. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.
19. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.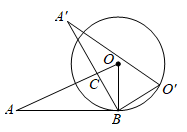 20. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .
20. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .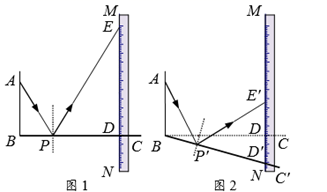 (1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.21. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .
(1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.21. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .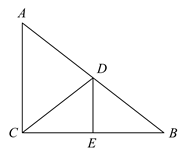 22. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .
22. 如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是 .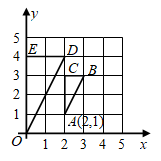 23. 如图, 中,点D为边BC的中点,连接AD,将 沿直线AD翻折至 所在平面内,得 ,连接 ,分别与边AB交于点E,与AD交于点O.若 , ,则AD的长为.
23. 如图, 中,点D为边BC的中点,连接AD,将 沿直线AD翻折至 所在平面内,得 ,连接 ,分别与边AB交于点E,与AD交于点O.若 , ,则AD的长为. 24. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)
24. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)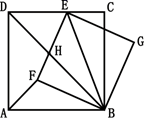 25. 如图,已知点 ,点B为直线 上的一动点,点 , , 于点C,连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时,n的值为.
25. 如图,已知点 ,点B为直线 上的一动点,点 , , 于点C,连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时,n的值为.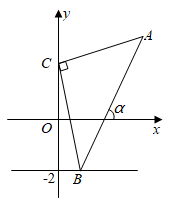
三、作图题
-
26. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
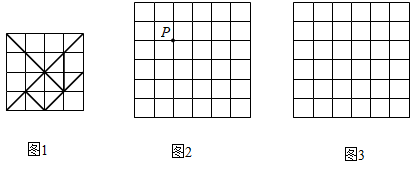 (1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.
(1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.四、综合题
-
27. 如图,在Rt 中, , 是 的平分线,以 为直径的 交 边于点E,连接 ,过点D作 ,交 于点F.
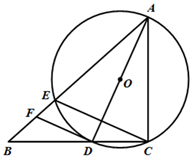 (1)、求证: 是 的切线;(2)、若 , ,求线段 的长.28. 如图,在 中, ,O为 边上一点,以O为圆心, 长为半径的 与 边相切于点D,交 于点E.
(1)、求证: 是 的切线;(2)、若 , ,求线段 的长.28. 如图,在 中, ,O为 边上一点,以O为圆心, 长为半径的 与 边相切于点D,交 于点E. (1)、求证: ;(2)、连接 ,若 , ,求线段 的长.29. 如图,在 中,点E、F分别在边 、 上,且 .
(1)、求证: ;(2)、连接 ,若 , ,求线段 的长.29. 如图,在 中,点E、F分别在边 、 上,且 .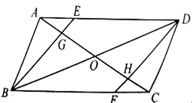 (1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.30. 如图,在 中,D在 上, , .
(1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.30. 如图,在 中,D在 上, , . (1)、求证: ∽ ;(2)、若 ,求 的值.31. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.
(1)、求证: ∽ ;(2)、若 ,求 的值.31. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
x … 0.30 0.80 1.60 2.40 3.20 4.00 4.80 5.60 … … 2.01 2.98 3.46 3.33 2.83 2.11 1.27 0.38 … … 5.60 4.95 3.95 2.96 2.06 1.24 0.57 0.10 … 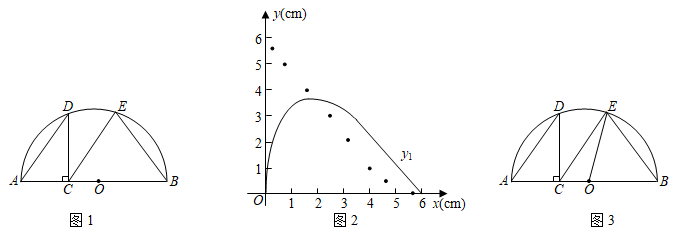 (1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.32. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
(1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.32. 问题:如图,在 中, , , , 的平分线AE,BF分别与直线CD交于点E,F,求EF的长.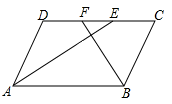
答案: .
(1)、探究:把“问题”中的条件“ ”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“ , ”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求 的值.33. 如图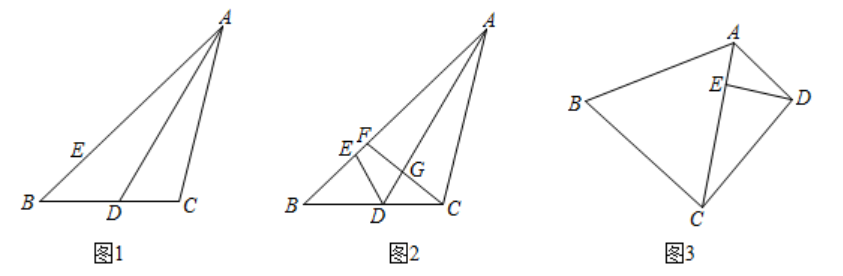 (1)、(证明体验)
(1)、(证明体验)如图1, 为 的角平分线, ,点E在 上, .求证: 平分 .
(2)、(思考探究)如图2,在(1)的条件下,F为 上一点,连结 交 于点G.若 , , ,求 的长.
(3)、(拓展延伸)如图3,在四边形 中,对角线 平分 ,点E在 上, .若 ,求 的长.
34. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .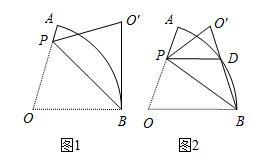 (1)、如图1,若 ,且 与 所在的圆相切于点B.
(1)、如图1,若 ,且 与 所在的圆相切于点B.①求 的度数.
②求AP的长.
(2)、如图2, 与 相交于点D,若点D为 的中点,且 ,求 的长.35. 如图, 内接于 是 的直径 的延长线上一点, .过圆心 作 的平行线交 的延长线于点 . (1)、求证: 是 的切线;(2)、若 ,求 的半径及 的值;36. 如图, 中, ,以点C为圆心, 为半径作 ,D为 上一点,连接 、 , , 平分 .
(1)、求证: 是 的切线;(2)、若 ,求 的半径及 的值;36. 如图, 中, ,以点C为圆心, 为半径作 ,D为 上一点,连接 、 , , 平分 . (1)、求证: 是 的切线;(2)、延长 、 相交于点E,若 ,求 的值.37. 一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm , BE=4cm . 当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)、求证: 是 的切线;(2)、延长 、 相交于点E,若 ,求 的值.37. 一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm , BE=4cm . 当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).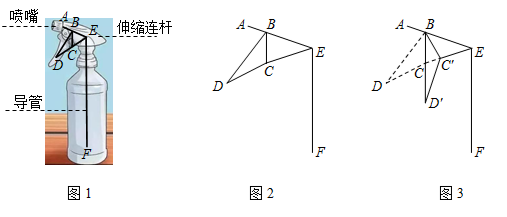
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
(1)、求点D转动到点D′的路径长;(2)、求点D到直线EF的距离(结果精确到0.1cm).38. 如图,直线l分别交x轴,y轴于A、B两点,交反比例函数 的图象于P、Q两点.若 ,且 的面积为4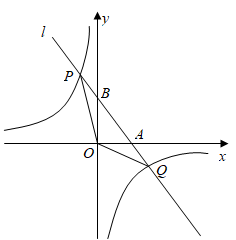 (1)、求k的值;(2)、当点P的横坐标为 时,求 的面积.
(1)、求k的值;(2)、当点P的横坐标为 时,求 的面积.
-

