全国历年中考数学真题精选汇编:图形变换与视图2
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
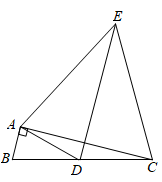 A、 B、 C、 D、22. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、 B、 C、 D、22. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )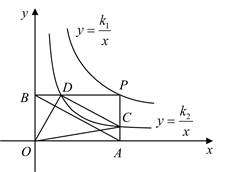 A、①② B、①③ C、②③ D、①
A、①② B、①③ C、②③ D、①二、填空题
-
3. 如图,在正方形 中,点O是对角线 的中点,点P在线段 上,连接 并延长交 于点E,过点P作 交 于点F,连接 、 , 交 于G,现有以下结论:① ;② ;③ ;④ 为定值;⑤ .以上结论正确的有(填入正确的序号即可).
 4. 如图,四边形 中, , , 于点D.若 , ,则线段 的长为.
4. 如图,四边形 中, , , 于点D.若 , ,则线段 的长为.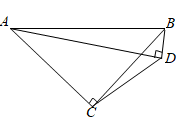 5. 如图、在正六边形 中,连接线 , , , , , 与 交于点M, 与 交于点为N, 与 交于点O,分别延长 , 于点G,设 .有以下结论:① ;② ;③ 的重心、内心及外心均是点M;④四边形 绕点O逆时针旋转 与四边形 重合.则所有正确结论的序号是.
5. 如图、在正六边形 中,连接线 , , , , , 与 交于点M, 与 交于点为N, 与 交于点O,分别延长 , 于点G,设 .有以下结论:① ;② ;③ 的重心、内心及外心均是点M;④四边形 绕点O逆时针旋转 与四边形 重合.则所有正确结论的序号是. 6. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.
6. 图1是邻边长为2和6的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图2),则图1中所标注的 的值为;记图1中小正方形的中心为点 , , ,图2中的对应点为点 , , .以大正方形的中心 为圆心作圆,则当点 , , 在圆内或圆上时,圆的最小面积为.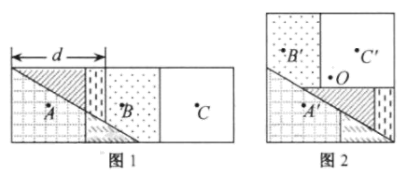 7. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
7. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.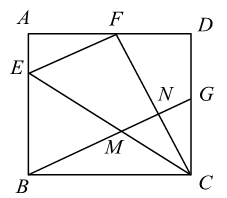 8. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
8. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
三、解答题
-
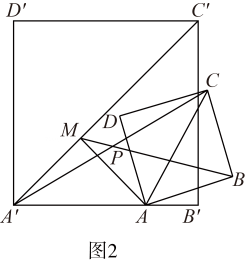
9. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
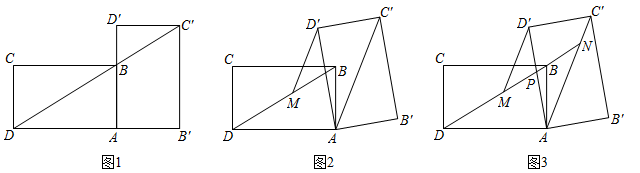
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
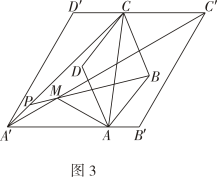
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
四、综合题
-
10. 如图1,在 中, , ,点D是 边上一点(含端点A、B),过点B作 垂直于射线 ,垂足为E,点F在射线 上,且 ,连接 、 .
 (1)、求证: ;(2)、如图2,连接 ,点P、M、N分别为线段 、 、 的中点,连接 、
(1)、求证: ;(2)、如图2,连接 ,点P、M、N分别为线段 、 、 的中点,连接 、、 .求 的度数及 的值;
(3)、在(2)的条件下,若 ,直接写出 面积的最大值.11. 如图1,在平面直角坐标系 中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点 的坐标值:x
…
0
1
2
3
…
y
…
0
3
4
3
0
…
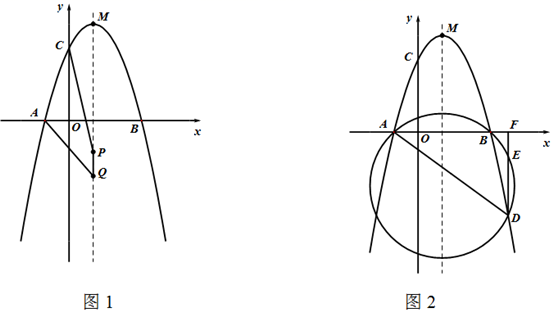 (1)、求出这条抛物线的解析式及顶点M的坐标;(2)、 是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值;(3)、如图2,点D是第四象限内抛物线上一动点,过点D作 轴,垂足为F, 的外接圆与 相交于点E.试问:线段 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.12. 已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周.
(1)、求出这条抛物线的解析式及顶点M的坐标;(2)、 是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值;(3)、如图2,点D是第四象限内抛物线上一动点,过点D作 轴,垂足为F, 的外接圆与 相交于点E.试问:线段 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.12. 已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周. (1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.13. 在矩形 中, , ,F是对角线 上不与点A,C重合的一点,过F作 于E,将 沿 翻折得到 ,点G在射线 上,连接 .(1)、如图1,若点A的对称点G落在 上, ,延长 交 于H,连接 .
(1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.13. 在矩形 中, , ,F是对角线 上不与点A,C重合的一点,过F作 于E,将 沿 翻折得到 ,点G在射线 上,连接 .(1)、如图1,若点A的对称点G落在 上, ,延长 交 于H,连接 .
①求证: ;
②求 .
(2)、如图2,若点A的对称点G落在 延长线上, ,判断 与 是否全等,并说明理由. 14. 如图,直线 与x轴交于点B,与y轴交于点A,点P为线段 的中点,点Q是线段 上一动点(不与点O、A重合).
14. 如图,直线 与x轴交于点B,与y轴交于点A,点P为线段 的中点,点Q是线段 上一动点(不与点O、A重合). (1)、请直接写出点A、点B、点P的坐标;(2)、连接 ,在第一象限内将 沿 翻折得到 ,点O的对应点为点E.若 ,求线段 的长;(3)、在(2)的条件下,设抛物线 的顶点为点C.
(1)、请直接写出点A、点B、点P的坐标;(2)、连接 ,在第一象限内将 沿 翻折得到 ,点O的对应点为点E.若 ,求线段 的长;(3)、在(2)的条件下,设抛物线 的顶点为点C.①若点C在 内部(不包括边),求a的取值范围;
②在平面直角坐标系内是否存在点C,使 最大?若存在,请直接写出点C的坐标;若不存在,请说明理由.
15. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).16. 某数学兴趣小组在数学课外活动中,对多边形内两要互相垂直的线段做了如下探究:(观察与猜想)
(1)、如图1,在正方形 中,点 , 分别是 , 上的两点,连接 , , ,则 的值为; (2)、如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为;
(2)、如图2,在矩形 中, , ,点 是 上的一点,连接 , ,且 ,则 的值为;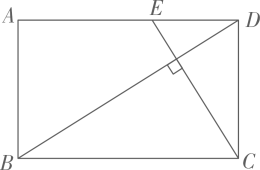 (3)、如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;
(3)、如图3,在四边形 中, ,点 为 上一点,连接 ,过点 作 的垂线交 的延长线于点 ,交 的延长线于点 ,求证: ;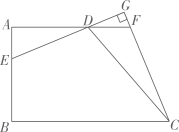 (4)、如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , ,且 .
(4)、如图4,在 中, , , ,将 沿 翻折,点 落在点 处得 ,点 , 分别在边 , 上,连接 , ,且 .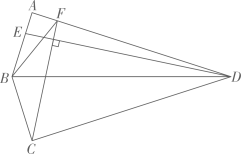
①求 的值;
②连接 ,若 ,直接写出 的长度.
17. 如图,在平面直角坐标系中,抛物线 交 轴于点 和 ,交 轴于点 ,抛物线的对称轴交 轴于点 ,交抛物线于点 .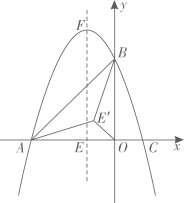 (1)、求抛物线的解析式;(2)、将线段 绕着点 沿顺时针方向旋转得到线段 ,旋转角为 ,连接 , ,求 的最小值.(3)、 为平面直角坐标系中一点,在抛物线上是否存在一点 ,使得以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的横坐标;若不存在,请说明理由;18. 如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 .
(1)、求抛物线的解析式;(2)、将线段 绕着点 沿顺时针方向旋转得到线段 ,旋转角为 ,连接 , ,求 的最小值.(3)、 为平面直角坐标系中一点,在抛物线上是否存在一点 ,使得以 , , , 为顶点的四边形为矩形?若存在,请直接写出点 的横坐标;若不存在,请说明理由;18. 如图,在 中, , 与 相交于点 ,与 相交于点 ,连接 ,已知 . (1)、求证: 为 的切线;(2)、若 , ,求 的长.19. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 .
(1)、求证: 为 的切线;(2)、若 , ,求 的长.19. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 . (1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.20. 如图,在等腰直角三角形 中, , ,边长为2的正方形 的对角线交点与点 重合,连接 , .
(1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.20. 如图,在等腰直角三角形 中, , ,边长为2的正方形 的对角线交点与点 重合,连接 , . (1)、求证: ;(2)、当点 在 内部,且 时,设 与 相交于点 ,求 的长;(3)、将正方形 绕点 旋转一周,当点 、 、 三点在同一直线上时,请直接写出 的长.21. 如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .
(1)、求证: ;(2)、当点 在 内部,且 时,设 与 相交于点 ,求 的长;(3)、将正方形 绕点 旋转一周,当点 、 、 三点在同一直线上时,请直接写出 的长.21. 如图,在 中, , ,点 为 的中点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,且 交线段 于点 , 的平分线 交 于点 .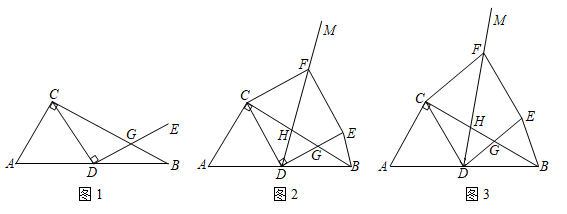 (1)、如图1,若 ,则线段 与 的数量关系是 , ;(2)、如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .
(1)、如图1,若 ,则线段 与 的数量关系是 , ;(2)、如图2,在(1)的条件下,过点 作 交 于点 ,连接 , .①试判断四边形 的形状,并说明理由;
②求证: ;
(3)、如图3,若 , ,过点 作 交 于点 ,连接 , ,请直接写出 的值(用含 的式子表示).22. 如图,BD是半径为3的⊙O的一条弦,BD=4 ,点A是⊙O上的一个动点(不与点B,D重合),以A,B,D为顶点作▱ABCD. (1)、如图2,若点A是劣弧 的中点.
(1)、如图2,若点A是劣弧 的中点.①求证:▱ABCD是菱形;
②求▱ABCD的面积.
(2)、若点A运动到优弧 上,且▱ABCD有一边与⊙O相切.①求AB的长;
②直接写出▱ABCD对角线所夹锐角的正切值.
23. 如图,锐角三角形ABC内接于⊙O,∠BAC的平分线AG交⊙O于点G,交BC边于点F,连结BG。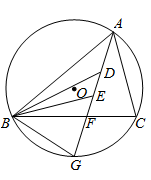 (1)、求证:△ABG∽△AFC;(2)、已知AB= ,AC=AF= ,求线段FG的长(用含 , 的代数式表示);(3)、已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,点E重合),∠ABD=∠CBE,求证: 。24. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .
(1)、求证:△ABG∽△AFC;(2)、已知AB= ,AC=AF= ,求线段FG的长(用含 , 的代数式表示);(3)、已知点E在线段AF上(不与点A,点F重合),点D在线段AE上(不与点A,点E重合),∠ABD=∠CBE,求证: 。24. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .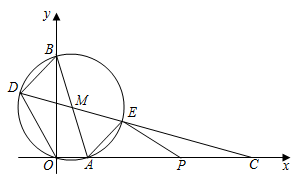 (1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.25. 如图,矩形ABCD中, ,点E是边AD的中点,点F是对角线BD上一动点, .连结EF,作点D关于直线EF的对称点P.
(1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.25. 如图,矩形ABCD中, ,点E是边AD的中点,点F是对角线BD上一动点, .连结EF,作点D关于直线EF的对称点P.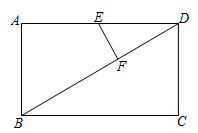 (1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.26. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、若 ,求DF的长.(2)、若 ,求DF的长.(3)、直线PE交BD于点Q,若 是锐角三角形,求DF长的取值范围.26. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.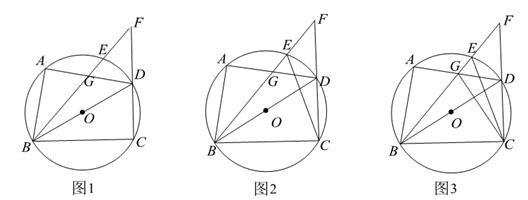 (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.
27. 在平面直角坐标系中,点A的坐标为 ,点B在直线 上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.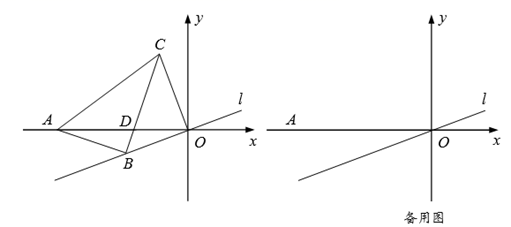 (1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.
(1)、如图,点B,C分别在第三、二象限内,BC与AO相交于点D.①若 ,求证: .
②若 ,求四边形 的面积.
(2)、是否存在点B,使得以 为顶点的三角形与 相似?若存在,求OB的长;若不存在,请说明理由.28. 如图,在平面直角坐标系中,抛物线 与坐标轴交于 两点,直线 交 轴于点 .点 为直线 下方抛物线上一动点,过点 作 轴的垂线,垂足为 分别交直线 于点 . (1)、求抛物线 的表达式;(2)、当 ,连接 ,求 的面积;(3)、① 是 轴上一点,当四边形 是矩形时,求点 的坐标;
(1)、求抛物线 的表达式;(2)、当 ,连接 ,求 的面积;(3)、① 是 轴上一点,当四边形 是矩形时,求点 的坐标;②在①的条件下,第一象限有一动点 ,满足 ,求 周长的最小值.
29. 探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.(1)、若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2倍?(填“存在”或“不存在”).(2)、继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;
②如图也可用反比例函数与一次函数证明 : , : ,那么,
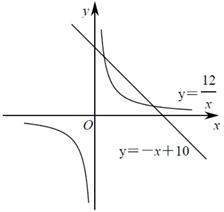
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
30. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.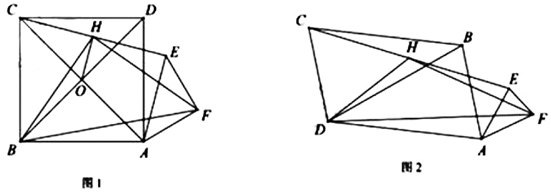 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
31. 在矩形 中, ,点 , 分别是边 、 上的动点,且 ,连接 ,将矩形 沿 折叠,点 落在点 处,点 落在点 处.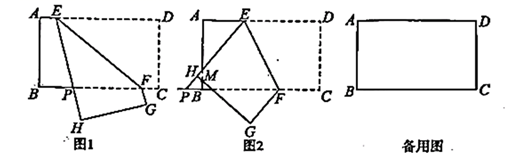 (1)、如图1,当 与线段 交于点 时,求证: ;(2)、如图2,当点 在线段 的延长线上时, 交 于点 ,求证:点 在线段 的垂直平分线上;(3)、当 时,在点 由点 移动到 中点的过程中,计算出点 运动的路线长.32. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.
(1)、如图1,当 与线段 交于点 时,求证: ;(2)、如图2,当点 在线段 的延长线上时, 交 于点 ,求证:点 在线段 的垂直平分线上;(3)、当 时,在点 由点 移动到 中点的过程中,计算出点 运动的路线长.32. 在一平面内,线段 ,线段 ,将这四条线段顺次首尾相接.把 固定,让 绕点 从 开始逆时针旋转角 到某一位置时, , 将会跟随出现到相应的位置.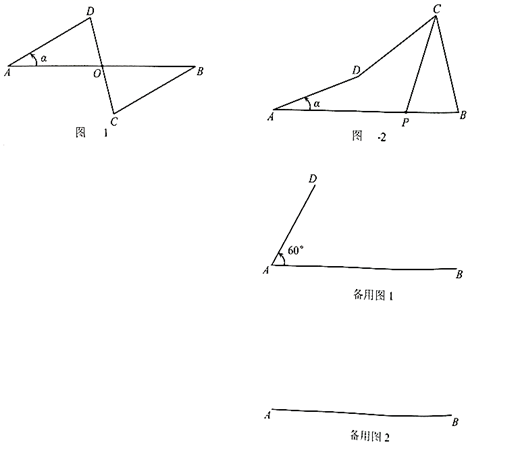 (1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);
(1)、论证 如图1,当 时,设 与 交于点 ,求证: ;(2)、发现当旋转角 时, 的度数可能是多少?(3)、尝试 取线段 的中点 ,当点 与点 距离最大时,求点 到 的距离;(4)、拓展 ①如图2,设点 与 的距离为 ,若 的平分线所在直线交 于点 ,直接写出 的长(用含 的式子表示);②当点 在 下方,且 与 垂直时,直接写出 的余弦值.
33. 如图1,O为半圆的圆心,C、D为半圆上的两点,且 .连接AC并延长,与BD的延长线相交于点E .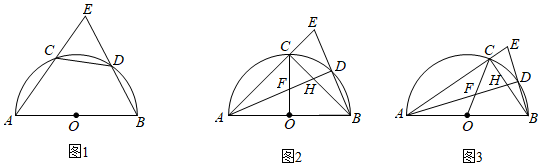 (1)、求证:CD=ED;(2)、AD与OC , BC分别交于点F , H .
(1)、求证:CD=ED;(2)、AD与OC , BC分别交于点F , H .①若CF=CH , 如图2,求证:CF•AF=FO•AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
34. 二次函数y=ax2+bx+4(a≠0)的图象经过点A(﹣4,0),B(1,0),与y轴交于点C , 点P为第二象限内抛物线上一点,连接BP、AC , 交于点Q , 过点P作PD⊥x轴于点D . (1)、求二次函数的表达式;(2)、连接BC , 当∠DPB=2∠BCO时,求直线BP的表达式;(3)、请判断: 是否有最大值,如有请求出有最大值时点P的坐标,如没有请说明理由.35. 如图1,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,DE∥AB,CF∥AD交线段AE于点F,连接BF.
(1)、求二次函数的表达式;(2)、连接BC , 当∠DPB=2∠BCO时,求直线BP的表达式;(3)、请判断: 是否有最大值,如有请求出有最大值时点P的坐标,如没有请说明理由.35. 如图1,在四边形ABCD中,∠ABC=∠BCD,点E在边BC上,且AE∥CD,DE∥AB,CF∥AD交线段AE于点F,连接BF. (1)、求证:△ABF≌△EAD;(2)、如图2,若AB=9,CD=5,∠ECF=∠AED,求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求 的值.36. 已知在平面直角坐标系xOy中,点A是反比例函数 图像上的一个动点,连结AO,AO的延长线交反比例函数 ( , )的图像于点B,过点A作AE⊥ 轴于点E。
(1)、求证:△ABF≌△EAD;(2)、如图2,若AB=9,CD=5,∠ECF=∠AED,求BE的长;(3)、如图3,若BF的延长线经过AD的中点M,求 的值.36. 已知在平面直角坐标系xOy中,点A是反比例函数 图像上的一个动点,连结AO,AO的延长线交反比例函数 ( , )的图像于点B,过点A作AE⊥ 轴于点E。 (1)、如图1,过点B作BF⊥ 轴于点F,连结EF,
(1)、如图1,过点B作BF⊥ 轴于点F,连结EF,①若 ,求证:四边形AEFO是平行四边形;
②连结BE,若 ,求△BOE的面积。
(2)、如图2,过点E作EP∥AB,交反比例函数 ( , )的图像于点P,连结OP。试探究:对于确定的实数 ,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由。
37. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 . (1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.38. 如图,四边形 是正方形,点 是射线 上的动点,连接 ,以 为对角线作正方形 ( 按逆时针排列),连接 .
(1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.38. 如图,四边形 是正方形,点 是射线 上的动点,连接 ,以 为对角线作正方形 ( 按逆时针排列),连接 .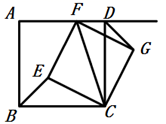 (1)、当点 在线段 上时.
(1)、当点 在线段 上时.①求证: ;
②求证: ;
(2)、设正方形 的面积为 ,正方形 的面积为 ,以 为原点的四边形的面积为 ,当 时,请直接写出 的值.39. 如图1 ,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过点 和点 从点,开始沿射线 方向以每秒 个单位长度的速度平移,平移后的三角形记为 (点 的对应点分别为点 ),平移时间为 秒,射线 交 轴于点 ,交抛物线于点 ,连接 .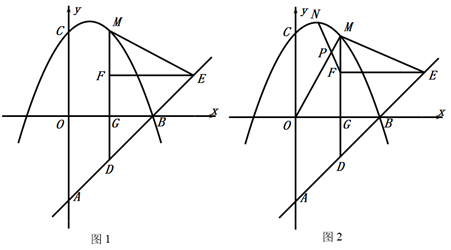 (1)、求抛物线的解析式;(2)、当 时,请直接写出 的值;(3)、如图2,点 在抛物线上,点 的横坐标是点 的横坐标的 ,连接 与 相交于点 ,当 时,求 的值.40. 已知:菱形 和菱形 , ,起始位置点 在边 上,点 在 所在直线上,点 在点 的右侧,点 在点 的右侧,连接 和 ,将菱形 以 为旋转中心逆时针旋转 角( ).(1)、如图1,若点 与 重合,且 ,求证: ;
(1)、求抛物线的解析式;(2)、当 时,请直接写出 的值;(3)、如图2,点 在抛物线上,点 的横坐标是点 的横坐标的 ,连接 与 相交于点 ,当 时,求 的值.40. 已知:菱形 和菱形 , ,起始位置点 在边 上,点 在 所在直线上,点 在点 的右侧,点 在点 的右侧,连接 和 ,将菱形 以 为旋转中心逆时针旋转 角( ).(1)、如图1,若点 与 重合,且 ,求证: ; (2)、若点 与 不重合, 是 上一点,当 时,连接 和 , 和 所在直线相交于点 ;
(2)、若点 与 不重合, 是 上一点,当 时,连接 和 , 和 所在直线相交于点 ;①如图2,当 时,请猜想线段 和线段 的数量关系及 的度数;
②如图3,当 时,请求出线段 和线段 的数量关系及 的度数;
③在②的条件下,若点 与 的中点重合, , ,在整个旋转过程中,当点 与点 重合时,请直接写出线段 的长.
-