全国历年中考数学真题精选汇编：命题与证明

试卷更新日期：2021-07-09 类型：二轮复习

进入出卷网下载

一、单选题

1. 定理：三角形的一个外角等于与它不相邻的两个内角的和．
已知：如图， $∠ A C D$ 是 $△ A B C$ 的外角．

求证： $∠ A C D = ∠ A + ∠ B$ ．

下列说法正确的是（）

A、证法1还需证明其他形状的三角形，该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证，就能证明该定理

查看试题解析
2. 下列四个选项中不是命题的是（）

A、对顶角相等 B、过直线外一点作直线的平行线 C、三角形任意两边之和大于第三边 D、如果 $a = b ， a = c$ ，那么 $b = c$

查看试题解析
3. 下列命题是真命题的是（）

A、一个角的补角一定大于这个角 B、平行于同一条直线的两条直线平行 C、等边三角形是中心对称图形 D、旋转改变图形的形状和大小

查看试题解析
4. 判断命题“如果n＜1，那么n²﹣1＜0”是假命题，只需举出一个反例.反例中的n可以为（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、0 D、 $\frac{1}{2}$

查看试题解析
5. 下列命题是假命题的是（）

A、平行四边形既是轴对称图形，又是中心对称图形 B、同角(或等角)的余角相等 C、线段垂直平分线上的点到线段两端的距离相等 D、正方形的对角线相等，且互相垂直平分

查看试题解析
6. 给出下列5个命题：①两点之间直线最短；②同位角相等；③等角的补角相等；④不等式组 ${\begin{matrix} x > - 2 \\ x < 2 \end{matrix}$ 的解集是﹣2＜x＜2；⑤对于函数y=﹣0.2x+11，y随x的增大而增大．其中真命题的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
7. 小柔要榨果汁，她有苹果、芭乐、柳丁三种水果，且其颗数比为9：7：6，小柔榨完果汁后，苹果、芭乐、柳丁的颗数比变为6：3：4，已知小柔榨果汁时没有使用柳丁，关于她榨果汁时另外两种水果的使用情形，下列叙述何者正确？（）

A、只使用苹果 B、只使用芭乐 C、使用苹果及芭乐，且使用的苹果颗数比使用的芭乐颗数多 D、使用苹果及芭乐，且使用的芭乐颗数比使用的苹果颗数多

查看试题解析
8. 已知下列命题：
①若a³＞b³ ，则a²＞b²；②若点A（x₁ ， y₁）和点B（x₂ ， y₂）在二次函数y=x²﹣2x﹣1的图象上，且满足x₁＜x₂＜1，则y₁＞y₂＞﹣2；③在同一平面内，a，b，c是直线，且a∥b，b⊥c，则a∥c；④周长相等的所有等腰直角三角形全等．其中真命题的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 甲、乙、丙、丁4人进行乒乓球单循环比赛（每两个人都要比赛一场），结果甲胜了丁，并且甲、乙、丙胜的场数相同，则丁胜的场数是（）

A、3 B、2 C、1 D、0

查看试题解析
10.
一个大矩形按如图方式分割成九个小矩形，且只有标号为①和②的两个小矩形为正方形．在满足条件的所有分割中，若知道九个小矩形中n个小矩形的周长，就一定能算出这个在大矩形的面积，则n的最小值是（）

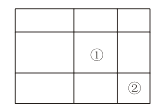A、3 B、4 C、5 D、6

查看试题解析
11. 下列命题中，假命题有（）
①两点之间线段最短；②到角的两边距离相等的点在角的平分线上；
③过一点有且只有一条直线与已知直线平行；④垂直于同一直线的两条直线平行；
⑤若⊙O的弦AB，CD交于点P，则PA•PB=PC•PD．

A、4个 B、3个 C、2个 D、1个

查看试题解析
12. 已知下列命题：
①若 $\frac{a}{b}$ ＞1，则a＞b；
②若a+b=0，则|a|=|b|；
③等边三角形的三个内角都相等；
④底角相等的两个等腰三角形全等．
其中原命题与逆命题均为真命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
13. 公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 $\sqrt{2}$ ，导致了第一次数学危机， $\sqrt{2}$ 是无理数的证明如下：
假设 $\sqrt{2}$ 是有理数，那么它可以表示成 $\frac{q}{p}$ （p与q是互质的两个正整数）．于是（ $\frac{q}{p}$ ）²=（ $\sqrt{2}$ ）²=2，所以，q²=2p² ．于是q²是偶数，进而q是偶数，从而可设q=2m，所以（2m）²=2p² ， p²=2m² ，于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾．从而可知“ $\sqrt{2}$ 是有理数”的假设不成立，所以， $\sqrt{2}$ 是无理数．
这种证明“ $\sqrt{2}$ 是无理数”的方法是（）

A、综合法 B、反证法 C、举反例法 D、数学归纳法

查看试题解析
14. 下列命题的逆命题不正确的是（　　）

A、平行四边形的对角线互相平分 B、两直线平行，内错角相等 C、等腰三角形的两个底角相等 D、对顶角相等

查看试题解析
15. 下列四个命题中，属于真命题的是（　　）

A、若 $\sqrt{a^{2}}$ =m，则a=m B、若a＞b，则am＞bm C、两个等腰三角形必定相似 D、位似图形一定是相似图形

查看试题解析
16. 下列命题中，属于真命题的是（）

A、同位角相等 B、正比例函数是一次函数 C、平分弦的直径垂直于弦 D、对角线相等的四边形是矩形

查看试题解析
17. 下列命题是真命题的有（）

①对顶角相等；
②两直线平行，内错角相等；
③两个锐角对应相等的两个直角三角形全等；
④有三个角是直角的四边形是矩形；
⑤平分弦的直径垂直于弦，并且平分弦所对的弧．

A、.1个 B、2个 C、3个 D、4个

查看试题解析
18. 如图，汽车在东西向的公路l上行驶，途中A，B，C，D四个十字路口都有红绿灯．AB之间的距离为800米，BC为1000米，CD为1400米，且l上各路口的红绿灯设置为：同时亮红灯或同时亮绿灯，每次红（绿）灯亮的时间相同，红灯亮的时间与绿灯亮的时间也相同．若绿灯刚亮时，甲汽车从A路口以每小时30千米的速度沿l向东行驶，同时乙汽车从D路口以相同的速度沿l向西行驶，这两辆汽车通过四个路口时都没有遇到红灯，则每次绿灯亮的时间可能设置为（）

A、50秒 B、45秒 C、40秒 D、35秒

查看试题解析
19. 下列选项中，可以用来证明命题“若a²＞1，则a＞1”是假命题的反例是（）

A、a=﹣2 B、a=﹣1 C、a=1 D、a=2

查看试题解析
20. 下列命题为真命题的是（）

A、有公共顶点的两个角是对顶角 B、多项式x²﹣4x因式分解的结果是x（x²﹣4） C、a+a=a² D、一元二次方程x²﹣x+2=0无实数根

查看试题解析
21. 下列命题是真命题的是（）

A、必然事件发生的概率等于0.5 B、5名同学二模的数学成绩是92，95，95，98，110，则他们的平均分是98分，众数是95 C、射击运动员甲、乙分别射击10次且击中环数的方差分别是5和18，则乙较甲稳定 D、要了解金牌获得者的兴奋剂使用情况，可采用抽样调查的方法

查看试题解析
22. 下列命题：
①对顶角相等；
②同位角相等，两直线平行；
③若a=b，则|a|=|b|；
④若x=0，则x²﹣2x=0
它们的逆命题一定成立的有（）

A、①②③④ B、①④ C、②④ D、②

查看试题解析
23. 下列命题中，真命题的个数是（　　）
①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
24. 已知命题“关于x的一元二次方程x²+bx+1=0，必有实数解”是假命题，则在下列选项中，b的值可以是（　　）

A、b=﹣3 B、b=﹣2 C、b=﹣1 D、b=2

查看试题解析
25. 下列命题是假命题的是（　　）

A、若|a|=|b|，则a=b B、两直线平行，同位角相等 C、对顶角相等 D、若b²﹣4ac＞0，则方程ax²+bx+c=0（a≠0）有两个不等的实数根

查看试题解析
26. 下列命题是假命题的是（　　）

A、经过两点有且只有一条直线 B、三角形的中位线平行且等于第三边的一半 C、平行四边形的对角线相等 D、圆的切线垂直于经过切点的半径

查看试题解析
27. 某届世界杯的小组比赛规则：四个球队进行单循环比赛（每两队赛一场），胜一场得3分，平一场得1分，负一场得0分，某小组比赛结束后，甲、乙，丙、丁四队分别获得第一，二，三，四名，各队的总得分恰好是四个连续奇数，则与乙打平的球队是（）

A、甲 B、甲与丁 C、丙 D、丙与丁

查看试题解析

二、填空题

28. 命题“三角形的三个内角中至少有两个锐角”是（填“真命题”或“假命题”）．

查看试题解析
29. 命题“四边相等的四边形是菱形”的逆命题是．

查看试题解析
30. 下列四个命题中：①对顶角相等；②同旁内角互补；③全等三角形的对应角相等；④两直线平行，同位角相等，其中假命题的有（填序号）

查看试题解析
31. 命题：“如果m是整数，那么它是有理数”，则它的逆命题为：．

查看试题解析
32. 命题“相等的角是对顶角”是命题（填“真”或“假”）

查看试题解析
33. 写出命题“如果a=b”，那么“3a=3b”的逆命题．

查看试题解析
34. 有下列4个命题：
①方程x²﹣（ $\sqrt{2}$ + $\sqrt{3}$ ）x+ $\sqrt{6}$ =0的根是 $\sqrt{2}$ 和 $\sqrt{3}$ ．
②在△ABC中，∠ACB=90°，CD⊥AB于D．若AD=4，BD= $\frac{9}{4}$ ，则CD=3．
③点P（x，y）的坐标x，y满足x²+y²+2x﹣2y+2=0，若点P也在y= $\frac{k}{x}$ 的图象上，则k=﹣1．
④若实数b、c满足1+b+c＞0，1﹣b+c＜0，则关于x的方程x²+bx+c=0一定有两个不相等的实数根，且较大的实数根x₀满足﹣1＜x₀＜1．
上述4个命题中，真命题的序号是．

查看试题解析
35. 命题“对角线相等的四边形是矩形”是命题（填“真”或“假”）．

查看试题解析
36. 请举反例说明命题“对于任意实数x，x²+5x+5的值总是正数”是假命题，你举的反例是x=（写出一个x的值即可）．

查看试题解析
37. 字母a，b，c，d各代表正方形、线段、正三角形、圆四个图形中的一种，将它们两两组合，并用字母连接表示，如表是三种组合与连接的对应表，由此可推断图形的连接方式为．

查看试题解析
38. 命题“直径所对的圆周角是直角”的逆命题是．

查看试题解析
39. 以下四个命题：
①对应角和面积都相等的两个三角形全等；
②“若x²﹣x=0，则x=0”的逆命题；
③若关于x、y的方程组 ${\begin{cases} - x + y - a = 0 \\ b x - y + 1 = 0 \end{cases}$ 有无数多组解，则a=b=1；
④将多项式5xy+3y﹣2x²y因式分解，其结果为﹣y（2x+1）（x﹣3）．
其中正确的命题的序号为．

查看试题解析

三、综合题

40. 今有甲、乙、丙三名候选人参与某村村长选举，共发出1800张选票，得票数最高者为当选人，且废票不计入任何一位候选人之得票数内，全村设有四个投开票所，目前第一、第二、第三投开票所已开完所有选票，剩下第四投开票所尚未开票，结果如表所示：
投开票所
候选人
废票
合计
甲
乙
丙
一
200
211
147
12
570
二
286
85
244
15
630
三
97
41
205
7
350
四

250
（单位：票）
请回答下列问题：

(1)、请分别写出目前甲、乙、丙三名候选人的得票数；

(2)、承（1），请分别判断甲、乙两名候选人是否还有机会当选村长，并详细解释或完整写出你的解题过程．

查看试题解析

投开票所	候选人			废票	合计
投开票所	甲	乙	丙	废票	合计
一	200	211	147	12	570
二	286	85	244	15	630
三	97	41	205	7	350
四					250