广西壮族自治区河池市宜州区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-07-09 类型:期中考试
一、单选题
-
1. 和数轴上的点一一对应的数是( )A、自然数 B、有理数 C、无理数 D、实数2. 平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在下列图形中, 与 是同位角的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 平面直角坐标系中,已知点 ,则点 到 轴的距离是( )A、2 B、-2 C、1 D、-16. 下列说法正确的是( )A、4的平方根是 B、最小的实数是0 C、两个无理数的和一定是无理数 D、负数没有立方根7. 计算: ( )A、 B、 C、 D、8. 约公元前5世纪的古希腊时期,由于“他”的发现导致了数学史上第一个无理数 的诞生,从而引发了第一次数学危机,这个“他”指的是( )A、毕达哥拉斯 B、希帕索斯 C、笛卡儿 D、苏格拉底9. 如图,三角形 中, , ,则图中能表示点到直线的距离的线段有( )条.
4. 下列计算正确的是( )A、 B、 C、 D、5. 平面直角坐标系中,已知点 ,则点 到 轴的距离是( )A、2 B、-2 C、1 D、-16. 下列说法正确的是( )A、4的平方根是 B、最小的实数是0 C、两个无理数的和一定是无理数 D、负数没有立方根7. 计算: ( )A、 B、 C、 D、8. 约公元前5世纪的古希腊时期,由于“他”的发现导致了数学史上第一个无理数 的诞生,从而引发了第一次数学危机,这个“他”指的是( )A、毕达哥拉斯 B、希帕索斯 C、笛卡儿 D、苏格拉底9. 如图,三角形 中, , ,则图中能表示点到直线的距离的线段有( )条.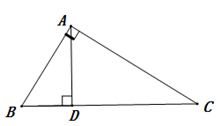 A、6 B、5 C、4 D、310. 如图,直线 , ,则 的度数为( )
A、6 B、5 C、4 D、310. 如图,直线 , ,则 的度数为( ) A、 B、 C、 D、11. 若点A(a+4,3a−2)到两坐标轴的距离相等,则 是( )A、3 B、-0.5 C、3或-0.5 D、1或-0.512. 如图,若直线 ,直线 分别与 、 相交,则有( )
A、 B、 C、 D、11. 若点A(a+4,3a−2)到两坐标轴的距离相等,则 是( )A、3 B、-0.5 C、3或-0.5 D、1或-0.512. 如图,若直线 ,直线 分别与 、 相交,则有( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如果座位表上“5列2行”记作 ,那么“4列3行”记为.14. 比较大小:-2 .15. 将直角三角板与两边平行的纸条如图放置,若 ,则 .
 16. 若点 在 轴上,则 .17. 如图,直角坐标系中 、 两点的坐标分别为 , ,则该坐标系内点 的坐标为.
16. 若点 在 轴上,则 .17. 如图,直角坐标系中 、 两点的坐标分别为 , ,则该坐标系内点 的坐标为. 18. 如图,三角形 是直角三角形 沿着 平移得到的,若 , , ,则图中阴影部分的面积为 .
18. 如图,三角形 是直角三角形 沿着 平移得到的,若 , , ,则图中阴影部分的面积为 .
三、解答题
-
19. 计算: .20. 求式中 的值: .21. 如图,平面直角坐标系中,点 为 ,将三角形 向左平移5个单位后再上平移1个单位得到三角形 .
 (1)、画出三角形 ;(2)、写出点 , , 的坐标;(3)、直接写出三角形 的面积: .22. 完善证明过程:请在横线上填写结论并在括号中注明理由.
(1)、画出三角形 ;(2)、写出点 , , 的坐标;(3)、直接写出三角形 的面积: .22. 完善证明过程:请在横线上填写结论并在括号中注明理由.已知:如图,直线 分别交 , 于点 , , , .

求证: .
证明:∵ (已知)
∴ ▲ ( )
∴▲ ( )
又∵ (已知)
∴ ,
即 ▲ .
∴▲ ( )
∴ ( )
23. 如图,已知点 、 、 、 均在三角形 的边上, , , .求证: . 24. 已知正数 的两个不等的平方根分别是 和 , 的立方根为-3; 是 的整数部分;(1)、求 和 的值;(2)、式子 的值 ;(3)、可判断 是数(填“有理”或“无理”).
24. 已知正数 的两个不等的平方根分别是 和 , 的立方根为-3; 是 的整数部分;(1)、求 和 的值;(2)、式子 的值 ;(3)、可判断 是数(填“有理”或“无理”).

