福建省莆田市仙游县郊尾、枫亭七校教研小片区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-07-09 类型:期中考试
一、单选题
-
1. 实数 ,0.8080080008中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 根据下列表述,能确定位置的是( )A、银泰影院2排 B、石家庄裕华路 C、北偏东30° D、东经118°,北纬40°3. 如图,射线 交于点 ,射线 平分 ,若 ,则 的度数为( )
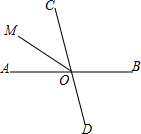 A、80° B、60° C、50° D、40°4. 若点 在第四象限内,则点 的坐标可能是( )A、 B、 C、 D、5. 下列各组数中,是二元一次方程 的解的是( )A、 B、 C、 D、6. 下列说法错误的是( )A、1的平方根是±1 B、–1的立方根是–1 C、 是2的算术平方根 D、-3是 的平方根7. 下列命题是假命题的( )A、在同一平面内,若a∥b,b∥c,则a∥c B、在同一平面内,若a⊥b,b∥c,则a⊥c C、在同一平面内,若a⊥b,b⊥c,则a⊥c D、在同一平面内,若a⊥b,b⊥c,则a∥c8. 由方程组 可得出x与y的关系式是( )A、x+y=8 B、x+y=1 C、x+y=-1 D、x+y=-89. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )A、 B、 C、 D、10. 如图,三个天平的托盘中形状相同的物体质量相等,图①②所示的两个天平处于平衡状态,要使第3个天平也保持平衡,则需在它的右盘中放置( )个球.
A、80° B、60° C、50° D、40°4. 若点 在第四象限内,则点 的坐标可能是( )A、 B、 C、 D、5. 下列各组数中,是二元一次方程 的解的是( )A、 B、 C、 D、6. 下列说法错误的是( )A、1的平方根是±1 B、–1的立方根是–1 C、 是2的算术平方根 D、-3是 的平方根7. 下列命题是假命题的( )A、在同一平面内,若a∥b,b∥c,则a∥c B、在同一平面内,若a⊥b,b∥c,则a⊥c C、在同一平面内,若a⊥b,b⊥c,则a⊥c D、在同一平面内,若a⊥b,b⊥c,则a∥c8. 由方程组 可得出x与y的关系式是( )A、x+y=8 B、x+y=1 C、x+y=-1 D、x+y=-89. 古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )A、 B、 C、 D、10. 如图,三个天平的托盘中形状相同的物体质量相等,图①②所示的两个天平处于平衡状态,要使第3个天平也保持平衡,则需在它的右盘中放置( )个球. A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
11. 在平面直角坐标系中,将点(2,3)向上平移2个单位,再向左平移1个单位,所得到的点的坐标为 .12. 方程x|a| – 1+(a-2)y=2是二元一次方程,则a=.13. 已知点 在第四象限,且到 轴的距离是1,到 轴的距离是3,则 的坐标是.14. 如图,将一张长方形纸片沿 折叠后,点 分别落在 的位置, 的延长线与 交于点G.若 ,则 .
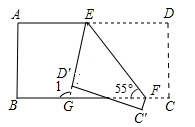 15. 若 , ,…, 是从0,1,2,这三个数中取值的一列数, , ,则在 , ,…, 中,取值为2的个数为.
15. 若 , ,…, 是从0,1,2,这三个数中取值的一列数, , ,则在 , ,…, 中,取值为2的个数为.三、解答题
-
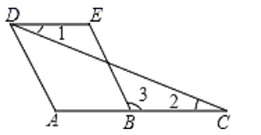
16.(1)、计算: ;(2)、解方程组17. 如图, , ,求证: .
请完成解答过程:
解:∵ (已知)
_▲_( )
又∵ (已知)
∴_▲_ _▲_( )
∴∠3=▲ ( )
∴ ( )
 18. 已知平面直角坐标系中有一点 .(1)、若点M到x轴的距离为1,请求出点M的坐标.(2)、若点 ,且 轴,请求出点M的坐标.19. 已知:(2x+5y+4) 2+|3x-4y-17|=0,求 的平方根.20. 如图,已知直线AB∥DF,∠D+∠B=180°.
18. 已知平面直角坐标系中有一点 .(1)、若点M到x轴的距离为1,请求出点M的坐标.(2)、若点 ,且 轴,请求出点M的坐标.19. 已知:(2x+5y+4) 2+|3x-4y-17|=0,求 的平方根.20. 如图,已知直线AB∥DF,∠D+∠B=180°.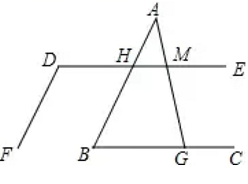 (1)、试说明DE∥BC;(2)、若∠AMD=75°,求∠AGC的度数.21. 如图,正方形网格中每个小正方形的边长都为1个单位长度,格点 的顶点 , ,现将 平移,把点 平移到点 ,点 , 分别是 , 的对应点.
(1)、试说明DE∥BC;(2)、若∠AMD=75°,求∠AGC的度数.21. 如图,正方形网格中每个小正方形的边长都为1个单位长度,格点 的顶点 , ,现将 平移,把点 平移到点 ,点 , 分别是 , 的对应点.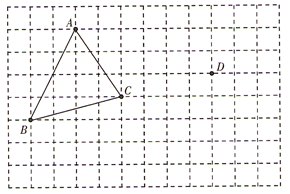 (1)、根据题意,在网格中建立平面直角坐标系;(2)、画出 ,点 的坐标为 ▲ ;(3)、描述 的平移过程.22. 某汽车公司有甲、乙两种货车可供租用,现有批货物要运往某地,货主准备租用该公司货车,已知甲、乙两种货车运货情况如下表:
(1)、根据题意,在网格中建立平面直角坐标系;(2)、画出 ,点 的坐标为 ▲ ;(3)、描述 的平移过程.22. 某汽车公司有甲、乙两种货车可供租用,现有批货物要运往某地,货主准备租用该公司货车,已知甲、乙两种货车运货情况如下表:第一次
第二次
甲种货车(辆)
2
5
乙种货车(辆)
3
6
累计运货(吨)
13
28
(1)、甲、乙两种货车每辆可装多少吨货物?(2)、若某货主共有20吨货物,计划租用该公司的货车,正好(每辆货车都满载)把这批货物运完,则该货主有几种租车方案?请说明理由.23. 阅读下列材料,解答下面的问题:我们知道方程 有无数个解,但在实际问题中往往只需求出其正整数解.例:由 ,得: ( 、 为正整数).要使 为正整数,则 为正整数,可知: 为3的倍数,从而 ,代入 .所以 的正整数解为 .问题:(1)、请你直接写出方程 的正整数解.(2)、若 为自然数,则求出满足条件的正整数 的值.(3)、关于 , 的二元一次方程组 的解是正整数,求整数 的值.24. 如图,已知在平面直角坐标系中,点 在 轴上,点 、 在 轴上, , , ,点 的坐标是 ,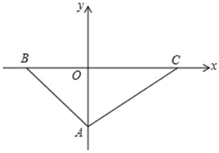 (1)、求 三个顶点 、 、 的坐标;(2)、连接 、 ,并用含字母 的式子表示 的面积( );(3)、在(2)问的条件下,是否存在点 ,使 的面积等于 的面积?如果存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求 三个顶点 、 、 的坐标;(2)、连接 、 ,并用含字母 的式子表示 的面积( );(3)、在(2)问的条件下,是否存在点 ,使 的面积等于 的面积?如果存在,请求出点 的坐标;若不存在,请说明理由.