全国历年中考数学真题精选汇编:圆2
试卷更新日期:2021-07-09 类型:二轮复习
一、填空题
-
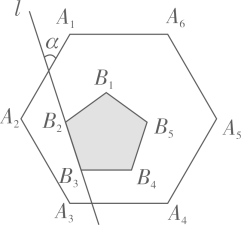
1. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
 2. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是.
2. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是.
二、综合题
-
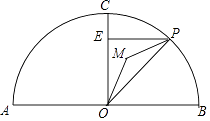
3. 如图,点 为以 为直径的半圆的圆心,点 , 在直径 上,点 , 在 上,四边形 为正方形,点 在 上运动(点 与点 , 不重合),连接 并延长交 的延长线于点 ,连接 交 于点 ,连接 .
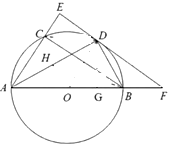
 (1)、求 的值;(2)、求 的值;(3)、令 , ,直径 ( , 是常数),求 关于 的函数解析式,并指明自变量 的取值范围.4. 如图,点D在以AB为直径的⊙O上,过D作⊙O的切线交AB延长线于点C,AE⊥CD于点E,交⊙O于点F,连接AD,FD.
(1)、求 的值;(2)、求 的值;(3)、令 , ,直径 ( , 是常数),求 关于 的函数解析式,并指明自变量 的取值范围.4. 如图,点D在以AB为直径的⊙O上,过D作⊙O的切线交AB延长线于点C,AE⊥CD于点E,交⊙O于点F,连接AD,FD.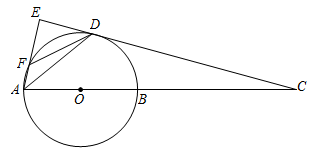 (1)、求证:∠DAE=∠DAC;(2)、求证:DF•AC=AD•DC;(3)、若sin∠C= ,AD=4 ,求EF的长.5. 如图, 的对角线 交于点E,以 为直径的 经过点E,与 交于点F,G是 延长线上一点,连接 ,交 于点H,且 .
(1)、求证:∠DAE=∠DAC;(2)、求证:DF•AC=AD•DC;(3)、若sin∠C= ,AD=4 ,求EF的长.5. 如图, 的对角线 交于点E,以 为直径的 经过点E,与 交于点F,G是 延长线上一点,连接 ,交 于点H,且 .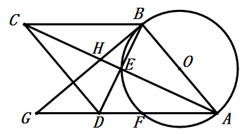 (1)、求证: 是 的切线;(2)、若 , ,求 的直径.6. 我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x﹣h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x﹣a)2+(y﹣b)2=r2 , 如:圆心为P(﹣2,1),半径为3的圆的方程为(x+2)2+(y﹣1)2=9.
(1)、求证: 是 的切线;(2)、若 , ,求 的直径.6. 我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x﹣h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x﹣a)2+(y﹣b)2=r2 , 如:圆心为P(﹣2,1),半径为3的圆的方程为(x+2)2+(y﹣1)2=9.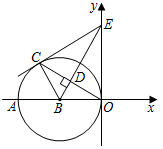 (1)、以M(﹣3,﹣1)为圆心, 为半径的圆的方程为 .(2)、如图,以B(﹣3,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC,垂足为D,延长BD交y轴于点E,已知sin∠AOC= .
(1)、以M(﹣3,﹣1)为圆心, 为半径的圆的方程为 .(2)、如图,以B(﹣3,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC,垂足为D,延长BD交y轴于点E,已知sin∠AOC= .①连接EC,证明:EC是⊙B的切线;
②在BE上是否存在一点Q,使QB=QC=QE=QO?若存在,求点Q的坐标,并写出以Q为圆心,以QB为半径的⊙Q的方程;若不存在,请说明理由.
7. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.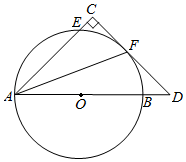 (1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.8. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的圆”,请研究如下美丽的圆,如图,Rt△ABC中,∠BCA=90°,AC=3,BC=4,点O在线段BC上,且OC= ,以O为圆心.OC为半径的⊙O交线段AO于点D,交线段AO的延长线于点E.
(1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.8. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的圆”,请研究如下美丽的圆,如图,Rt△ABC中,∠BCA=90°,AC=3,BC=4,点O在线段BC上,且OC= ,以O为圆心.OC为半径的⊙O交线段AO于点D,交线段AO的延长线于点E.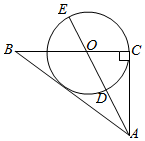 (1)、求证:AB是⊙O的切线;(2)、研究过短中,小明同学发现 = ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.9. 如图, 是⊙O的直径,E,C是 上两点,且 ,连接 , ,过点C作 交 的延长线于点D.
(1)、求证:AB是⊙O的切线;(2)、研究过短中,小明同学发现 = ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.9. 如图, 是⊙O的直径,E,C是 上两点,且 ,连接 , ,过点C作 交 的延长线于点D. (1)、判定直线 与⊙O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.10. 如图所示: 与 的边 相切于点C,与 、 分别交于点D、E, . 是 的直径.连接 ,过C作 交 于G,连接 、 , 与 交于点F.
(1)、判定直线 与⊙O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.10. 如图所示: 与 的边 相切于点C,与 、 分别交于点D、E, . 是 的直径.连接 ,过C作 交 于G,连接 、 , 与 交于点F.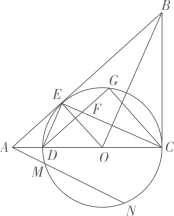 (1)、求证:直线 与 相切;(2)、求证: ;(3)、若 时,过A作 交 于M、N两点(M在线段 上),求 的长.11. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.
(1)、求证:直线 与 相切;(2)、求证: ;(3)、若 时,过A作 交 于M、N两点(M在线段 上),求 的长.11. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把 的值称为⊙I关于直线a的“特征数”.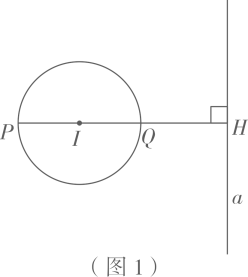
 (1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.
(1)、如图2,在平面直角坐标系 中,点E的坐标为 ,半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_▲__(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_▲__;
②若直线n的函数表达式为 ,求 关于直线n的“特征数”;
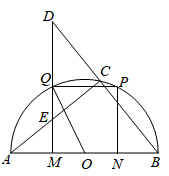
(2)、在平面直角坐标系 中,直线l经过点 ,点F是坐标平面内一点,以F为圆心, 为半径作⊙F.若⊙F与直线l相离,点 是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是 ,求直线l的函数表达式.12. 已知 内接于 , , 的平分线与 交于点D,与 交于点E,连接 并延长与 过点A的切线交于点F,记 .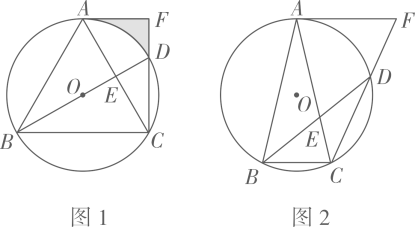 (1)、如图1,若 ,
(1)、如图1,若 ,①直接写出 的值为;
②当 的半径为2时,直接写出图中阴影部分的面积为;
(2)、如图2,若 ,且 , ,求 的长.13. 定义:有一组对角互余的四边形叫做对余四边形.(1)、理解:若四边形 是对余四边形,则 与 的度数之和为;(2)、证明:如图1, 是 的直径,点 在 上, , 相交于点D.求证:四边形 是对余四边形;
 (3)、探究:如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由.
(3)、探究:如图2,在对余四边形 中, , ,探究线段 , 和 之间有怎样的数量关系?写出猜想,并说明理由. 14. 如图,在 中, ,以 为直径的⊙O交 于点D, 与过点D的切线互相垂直,垂足为E.
14. 如图,在 中, ,以 为直径的⊙O交 于点D, 与过点D的切线互相垂直,垂足为E. (1)、求证: 平分 ;(2)、若 ,求 的值.15. 如图, 是 的直径,直线 与 相切于点A,直线 与 相切于点B,点C(异于点A)在 上,点D在 上,且 ,延长 与 相交于点E,连接 并延长交 于点F.
(1)、求证: 平分 ;(2)、若 ,求 的值.15. 如图, 是 的直径,直线 与 相切于点A,直线 与 相切于点B,点C(异于点A)在 上,点D在 上,且 ,延长 与 相交于点E,连接 并延长交 于点F.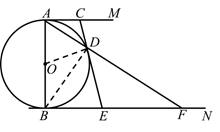 (1)、求证: 是 的切线;(2)、求证: ;(3)、如图,连接 并延长与 分别相交于点G、H,连接 .若 , ,求 .
(1)、求证: 是 的切线;(2)、求证: ;(3)、如图,连接 并延长与 分别相交于点G、H,连接 .若 , ,求 .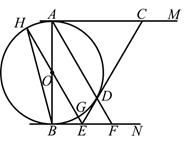 16. 如图,在⊙O中,AB为⊙O的直径,C为⊙O上一点,P是 的中点,过点P作AC的垂线,交AC的延长线于点D.
16. 如图,在⊙O中,AB为⊙O的直径,C为⊙O上一点,P是 的中点,过点P作AC的垂线,交AC的延长线于点D.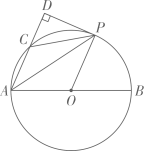 (1)、求证:DP是⊙O的切线;(2)、若AC=5,sin∠APC= ,求AP的长.17. 如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC的中点,连接EF.
(1)、求证:DP是⊙O的切线;(2)、若AC=5,sin∠APC= ,求AP的长.17. 如图,已知AC,BD为⊙O的两条直径,连接AB,BC,OE⊥AB于点E,点F是半径OC的中点,连接EF.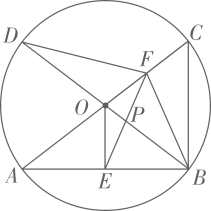 (1)、设⊙O的半径为1,若∠BAC=30°,求线段EF的长。(2)、连接BF,DF
(1)、设⊙O的半径为1,若∠BAC=30°,求线段EF的长。(2)、连接BF,DF①求证:PE=PF
②若DF=EF,求∠BAC的度数。
18. 如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA.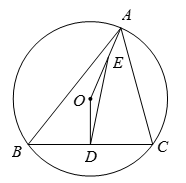 (1)、若∠BAC=60°,
(1)、若∠BAC=60°,①求证:OD= OA.
②当OA=1时,求△ABC面积的最大值。
(2)、点E在线段OA上,(OE=OD.连接DE,设∠ABC=m∠OED.∠ACB=n∠OED(m,n是正数).若∠ABC<∠ACB,求证:m-n+2=0.
19. 如图1, O经过等边△ABC的顶点A,C(圆心O在△ABC内),分别与AB,CB的延长线交于点D,E,连结DE,BF⊥EC交AE于点F.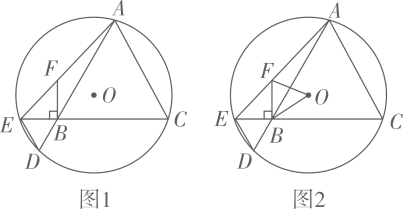 (1)、求证:BD=BE.(2)、当AF:EF=3:2,AC=6时,求AE的长。(3)、设 =x,tan∠DAE=y.
(1)、求证:BD=BE.(2)、当AF:EF=3:2,AC=6时,求AE的长。(3)、设 =x,tan∠DAE=y.①求y关于x的函数表达式;
②如图2,连结OF,OB,若△AEC的面积是△OFB面积的10倍,求y的值
20. 已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A(-3,0),B(0,3).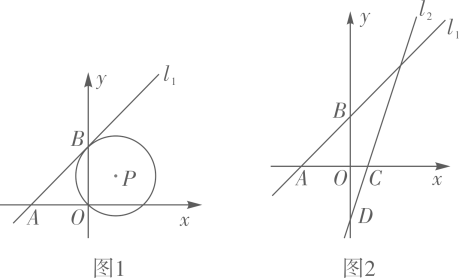 (1)、如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;(2)、如图2,已知直线l2: y=3x-3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心, 为半径画圆.
(1)、如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;(2)、如图2,已知直线l2: y=3x-3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心, 为半径画圆.①当点Q与点C重合时,求证: 直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点, 连结QM,QN. 问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.
21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且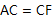 ,连接FB,FD,FD交AB于点N.
,连接FB,FD,FD交AB于点N. 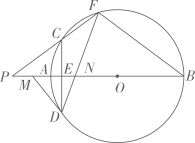 (1)、若AE=1,CD=6,求⊙O的半径;(2)、求证:△BNF为等腰三角形;(3)、连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON·OP=OE·OM.22. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B.
(1)、若AE=1,CD=6,求⊙O的半径;(2)、求证:△BNF为等腰三角形;(3)、连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ON·OP=OE·OM.22. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1,以边AC上一点O为圆心,OA为半径的⊙O经过点B. (1)、求⊙O的半径;(2)、点P为 中点,作PQ⊥AC,垂足为Q,求OQ的长;(3)、在(2)的条件下,连接PC,求tan∠PCA的值.23. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,点 在 的延长线上,且 .
(1)、求⊙O的半径;(2)、点P为 中点,作PQ⊥AC,垂足为Q,求OQ的长;(3)、在(2)的条件下,连接PC,求tan∠PCA的值.23. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,点 在 的延长线上,且 . (1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.24. 如图, 是⊙ 的直径,点 和点 是⊙ 上的两点,连接 , , ,过点 作射线交 的延长线于点 ,使 .
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.24. 如图, 是⊙ 的直径,点 和点 是⊙ 上的两点,连接 , , ,过点 作射线交 的延长线于点 ,使 . (1)、求证: 是⊙ 的切线;(2)、若 ,求阴影部分的面积.25. 如图, 是 的直径,点 为 上一点,点 是半径 上一动点(不与 , 重合),过点 作射线 ,分别交弦 , 于 , 两点,在射线 上取点 ,使 .
(1)、求证: 是⊙ 的切线;(2)、若 ,求阴影部分的面积.25. 如图, 是 的直径,点 为 上一点,点 是半径 上一动点(不与 , 重合),过点 作射线 ,分别交弦 , 于 , 两点,在射线 上取点 ,使 . (1)、求证: 是 的切线;(2)、当点 是 的中点时,
(1)、求证: 是 的切线;(2)、当点 是 的中点时,①若 ,判断以 , , , 为顶点的四边形是什么特殊四边形,并说明理由;
②若 ,且 ,求 的长.
26. 如图1,四边形 内接于圆 , 是圆 的直径,过点 的切线与 的延长线相交于点 .且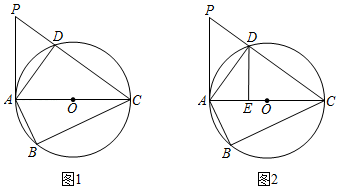 (1)、求证: ;(2)、过图1中的点 作 ,垂足为 (如图2),当 , 时,求圆 的半径.27. 如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED= .
(1)、求证: ;(2)、过图1中的点 作 ,垂足为 (如图2),当 , 时,求圆 的半径.27. 如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED= .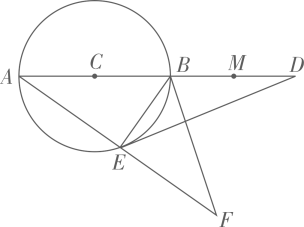 (1)、求证:△DEB∽△DAE;(2)、求DA,DE的长;(3)、若点F在B、E、M三点确定的圆上,求MD的长.28. 如图,点 为正方形 的对角线 上的一点,连接 并延长交 于点 ,交 的延长线于点 , 是 的外接圆,连接 .
(1)、求证:△DEB∽△DAE;(2)、求DA,DE的长;(3)、若点F在B、E、M三点确定的圆上,求MD的长.28. 如图,点 为正方形 的对角线 上的一点,连接 并延长交 于点 ,交 的延长线于点 , 是 的外接圆,连接 . (1)、求证: 是 的切线;(2)、若 ,正方形 的边长为 ,求 的半径和线段 的长.29. 已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是O的两条弦,AB⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.
(1)、求证: 是 的切线;(2)、若 ,正方形 的边长为 ,求 的半径和线段 的长.29. 已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是O的两条弦,AB⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P. (1)、如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)、如图2,连接ME、OA,OA与ME交于点Q,若0A⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)、如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN交于点R,连接RG,若HK:ME=2:3,BC= ,求RG的长.30. 如图,BM是以AB为直径的⊙O的切线,B为切点,BC平分∠ABM,弦CD交AB于点E,DE=OE.
(1)、如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)、如图2,连接ME、OA,OA与ME交于点Q,若0A⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)、如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN交于点R,连接RG,若HK:ME=2:3,BC= ,求RG的长.30. 如图,BM是以AB为直径的⊙O的切线,B为切点,BC平分∠ABM,弦CD交AB于点E,DE=OE. (1)、求证:△ACB是等腰直角三角形;(2)、求证:OA2=OE•DC:(3)、求tan∠ACD的值.31. 如图, 中, ,以 为直径的⊙ 交 于点 ,点 为 延长线上一点,且 .
(1)、求证:△ACB是等腰直角三角形;(2)、求证:OA2=OE•DC:(3)、求tan∠ACD的值.31. 如图, 中, ,以 为直径的⊙ 交 于点 ,点 为 延长线上一点,且 .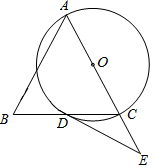 (1)、求证: 是⊙ 的切线;(2)、若 ,求⊙ 的半径.32. 已知△ABC内接于⊙O , ∠BAC的平分线交⊙O于点D , 连接DB , DC .
(1)、求证: 是⊙ 的切线;(2)、若 ,求⊙ 的半径.32. 已知△ABC内接于⊙O , ∠BAC的平分线交⊙O于点D , 连接DB , DC .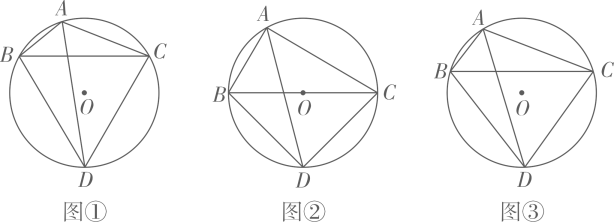 (1)、如图①,当∠BAC =120°时,请直接写出线段AB , AC , AD之间满足的等量关系式:;(2)、如图②,当∠BAC =90°时,试探究线段AB , AC , AD之间满足的等量关系,并证明你的结论;(3)、如图③,若BC=5,BD=4,求 的值.33. 主题学习
(1)、如图①,当∠BAC =120°时,请直接写出线段AB , AC , AD之间满足的等量关系式:;(2)、如图②,当∠BAC =90°时,试探究线段AB , AC , AD之间满足的等量关系,并证明你的结论;(3)、如图③,若BC=5,BD=4,求 的值.33. 主题学习通过对下面数学模型的研究学习,解决(1)(2)题
【模型呈现】
如图,在Rt△ABC中,∠ACB=90°,将斜边AB绕点A顺时针旋转90°得到AD,过点D作DE⊥AC于点E,可以推理得到△ABC≌△DAE,进而得到AC=DE,BC=AE
我们把这个数学模型称为“K型”,
推理过程如下: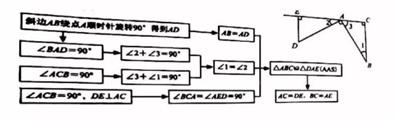
【模型应用】如图,Rt△ABC内接于⊙O,∠ACB=90°,BC=2.将斜边AB绕点A顺时针旋转一定角度得到AD,过点D作DE⊥AC于点E,∠DAE=∠ABC,DE=1,连接DO交⊙O于点F.
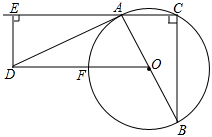 (1)、求证:AD是⊙O的切线;(2)、接FC交AB于点G,连接FB,求证:FG2=GO·GB.
(1)、求证:AD是⊙O的切线;(2)、接FC交AB于点G,连接FB,求证:FG2=GO·GB.
34. 如图, 是⊙ 的直径,点 在 的延长线上, 、 是⊙ 上的两点, , ,延长 交 的延长线于点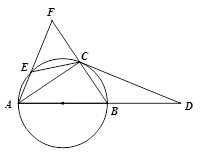 (1)、求证: 是⊙ 的切线;(2)、求证:(3)、若 , ,求弦 的长.35. 如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
(1)、求证: 是⊙ 的切线;(2)、求证:(3)、若 , ,求弦 的长.35. 如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE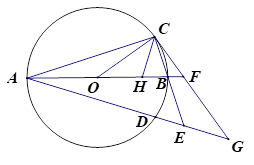 (1)、求证:直线CG为⊙O的切线;(2)、若点H为线段OB上一点,连接CH,满足CB=CH,
(1)、求证:直线CG为⊙O的切线;(2)、若点H为线段OB上一点,连接CH,满足CB=CH,①△CBH∽△OBC
②求OH+HC的最大值
36. 如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.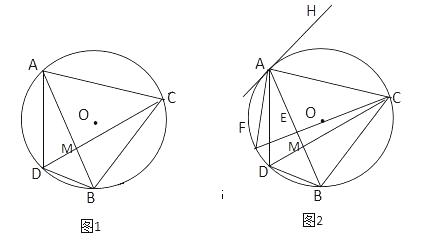 (1)、求证:AC=BC;(2)、如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.37. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)、求证:AC=BC;(2)、如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.37. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.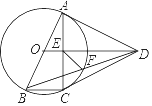 (1)、证明:OD∥BC;(2)、若tan∠ABC=2,证明:DA与⊙O相切;
(1)、证明:OD∥BC;(2)、若tan∠ABC=2,证明:DA与⊙O相切;
(3)、在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.38. 如图,AB 是⊙M 的直径,BC 是⊙M 的切线,切点为 B,C 是 BC 上(除 B 点外)的任意一点,连接 CM 交⊙M 于点 G,过点 C 作 DC⊥BC 交 BG 的 延长线于点 D,连接 AG 并延长交 BC 于点 E.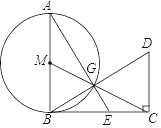 (1)、求证:△ABE∽△BCD;
(1)、求证:△ABE∽△BCD;
(2)、若 MB=BE=1,求 CD 的长度.