全国历年中考数学真题精选汇编:圆1
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )
 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD2. 如图,等腰 中,顶角 ,用尺规按①到④的步骤操作:
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD2. 如图,等腰 中,顶角 ,用尺规按①到④的步骤操作: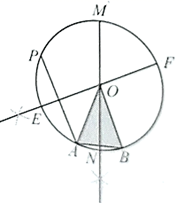
①以 为圆心, 为半径画圆;
②在 上任取一点 (不与点 , 重合),连接 ;
③作 的垂直平分线与 交于 , ;
④作 的垂直平分线与 交于 , .
结论Ⅰ:顺次连接 , , , 四点必能得到矩形;
结论Ⅱ: 上只有唯一的点 ,使得 .
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
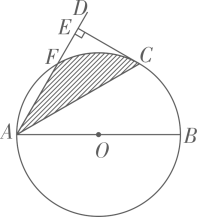
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对3. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )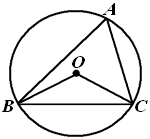 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值4. 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值4. 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )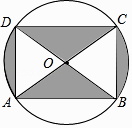 A、5πcm2 B、10πcm2 C、15πcm2 D、20πcm25. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( )
A、5πcm2 B、10πcm2 C、15πcm2 D、20πcm25. 如图, 是 的直径, 是弦,点 在直径 的两侧.若 , ,则 的长为( ) A、 B、 C、 D、6. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).
A、 B、 C、 D、6. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).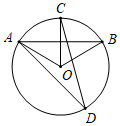 A、30° B、40° C、50° D、60°7. 如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )
A、30° B、40° C、50° D、60°7. 如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )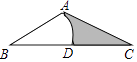 A、2﹣ B、2﹣ C、4﹣ D、4﹣8. 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A、2﹣ B、2﹣ C、4﹣ D、4﹣8. 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( ) A、26π B、13π C、 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( )
A、26π B、13π C、 D、9. 如图, 为⊙ 的直径,C,D是圆周上的两点,若 ,则锐角 的度数为( ) A、57° B、52° C、38° D、26°10. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )
A、57° B、52° C、38° D、26°10. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )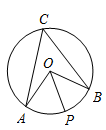 A、30° B、45° C、55° D、60°11. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )
A、30° B、45° C、55° D、60°11. 如图,四边形 内接于 ,连接 .若 , ,则 的度数是( )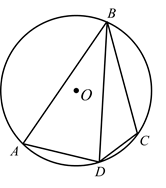 A、125° B、130° C、135° D、140°12. 已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是( )A、11 B、10 C、9 D、813. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、14. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切15. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )
A、125° B、130° C、135° D、140°12. 已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是( )A、11 B、10 C、9 D、813. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、14. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切15. 如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )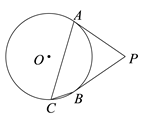 A、55° B、70° C、110° D、125°16. 如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD等于( )
A、55° B、70° C、110° D、125°16. 如图,AB是⊙O的直径,BC与⊙O相切于点B,AC交⊙O于点D,若∠ACB=50°,则∠BOD等于( ) A、40° B、50° C、60° D、80°17. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、1
A、40° B、50° C、60° D、80°17. 用一个半径为 面积为 的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径为( )A、 B、 C、2 D、1二、填空题
-
18. 如图,点 , , , 在 上, , , ,则 .
 19. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= .
19. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= . 20. 半径为10cm的半圆围成一个圆锥,则这个圆锥的高是cm.21. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在 上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.
20. 半径为10cm的半圆围成一个圆锥,则这个圆锥的高是cm.21. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在 上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.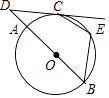 22. 我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)23. 如图,⊙O是 的外接圆, , ,则 的长为.
22. 我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为 . (用含m,n的式子表示)23. 如图,⊙O是 的外接圆, , ,则 的长为. 24. 已知圆锥的底面圆的半径是2.5,母线长是9,其侧面展开图的圆心角是度.25. 如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是 .
24. 已知圆锥的底面圆的半径是2.5,母线长是9,其侧面展开图的圆心角是度.25. 如图,已知Rt△ABC,∠C=90°,AC=3,BC=4.分别以点A、B为圆心画圆.如果点C在⊙A内,点B在⊙A外,且⊙B与⊙A内切,那么⊙B的半径长r的取值范围是 .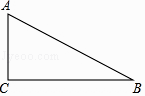 26. 已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为.27. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 .
26. 已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为.27. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 . 28. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.29. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )
28. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.29. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )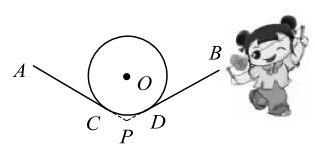
三、综合题
-
30. 在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G, 的平分线交图形G于点D,连接AD,CD.
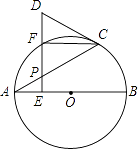
 (1)、求证:AD=CD;(2)、过点D作DE BA,垂足为E,作DF BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.31. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
(1)、求证:AD=CD;(2)、过点D作DE BA,垂足为E,作DF BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.31. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
5
6
y/cm
0
2.0
2.3
2.1
0.9
0
(说明:补全表格时相关数值保留一位小数)
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象. (3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.32. 已知 是 的直径,弦 与 相交, .
(3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.32. 已知 是 的直径,弦 与 相交, . (1)、如图①,若 为
(1)、如图①,若 为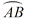 的中点,求 和 的大小;
的中点,求 和 的大小;
(2)、如图②,过点 作 的切线,与 的延长线交于点 ,若 ,求 的大小.33. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)、如图①,求∠T和∠CDB的大小;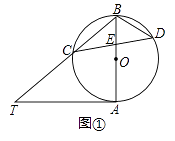 (2)、如图②,当BE=BC时,求∠CDO的大小.
(2)、如图②,当BE=BC时,求∠CDO的大小.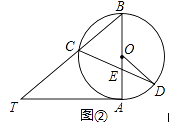 34. 如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 ( 为1~12的整数),过点 作 的切线交 延长线于点 .
34. 如图, 的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为 ( 为1~12的整数),过点 作 的切线交 延长线于点 . (1)、通过计算比较直径和劣弧 长度哪个更长;(2)、连接 ,则 和 有什么特殊位置关系?请简要说明理由;(3)、求切线长 的值.35.
(1)、通过计算比较直径和劣弧 长度哪个更长;(2)、连接 ,则 和 有什么特殊位置关系?请简要说明理由;(3)、求切线长 的值.35.如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
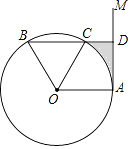 (1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).36. 如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).36. 如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.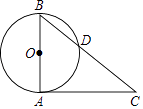 (1)、求∠B的度数.(2)、求 的长.(结果保留π)37. 如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 .
(1)、求∠B的度数.(2)、求 的长.(结果保留π)37. 如图,四边形 内接于 , ,延长 到点 ,使得 ,连接 . (1)、求证: ;(2)、若 , , ,求 的值.38. 如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M. E是线段CM上的点,连接BE. F是△BDE的外接圆与AD的另一个交点,连接EF, BF
(1)、求证: ;(2)、若 , , ,求 的值.38. 如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M. E是线段CM上的点,连接BE. F是△BDE的外接圆与AD的另一个交点,连接EF, BF
 (1)、求证:△BEF是直角三角形;(2)、求证:△BEF∽△BCA;(3)、当AB=6,BC=m时,在线段CM中存在点E,使得EF和AB互相平分,求m的值.
(1)、求证:△BEF是直角三角形;(2)、求证:△BEF∽△BCA;(3)、当AB=6,BC=m时,在线段CM中存在点E,使得EF和AB互相平分,求m的值.