全国历年中考数学真题精选汇编:四边形2
试卷更新日期:2021-07-09 类型:二轮复习
一、单选题
-
1.
如图,在▱ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
 A、 B、2 C、2 D、42. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG, 的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为( )
A、 B、2 C、2 D、42. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG, 的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为( ) A、 B、 C、13 D、163. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
A、 B、 C、13 D、163. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( ) A、3 B、4 C、2 D、34. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )
A、3 B、4 C、2 D、34. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( ) A、①② B、①③ C、①②③ D、②③④5. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )
A、①② B、①③ C、①②③ D、②③④5. 如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=b﹣ ;③△ABM≌△NGF;④S四边形AMFN=a2+b2;⑤A,M,P,D四点共圆,其中正确的个数是( )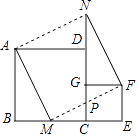 A、2 B、3 C、4 D、56. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )
A、2 B、3 C、4 D、56. 有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )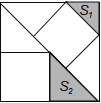 A、1: B、1:2 C、2:3 D、4:97. 如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A、1: B、1:2 C、2:3 D、4:97. 如图,EF过▱ABCD对角线的交点O,交AD于E,交BC于F,若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( ) A、14 B、13 C、12 D、108. 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
A、14 B、13 C、12 D、108. 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )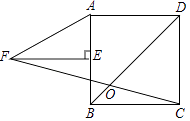 A、60° B、67.5° C、75° D、54°
A、60° B、67.5° C、75° D、54°二、填空题
-
9. 已知一个多边形的每一个外角都等于 ,则这个多边形的边数是 .10. 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .
 11. 图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中 ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为 cm.
11. 图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中 ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为 cm. 12. 如图,矩形 中, 、 交于点 , 、 分别为 、 的中点.若 ,则 的长为.
12. 如图,矩形 中, 、 交于点 , 、 分别为 、 的中点.若 ,则 的长为. 13. 如图,四边形 中, 平分 , , 、 分别为 、 的中点, ,则 的度数为.(用含 的式子表示)
13. 如图,四边形 中, 平分 , , 、 分别为 、 的中点, ,则 的度数为.(用含 的式子表示) 14. 四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE= ,则CE的长为 .15. 如图,在矩形ABCD中,AB= ,E是BC的中点,AE⊥BD于点F,则CF的长是 .
14. 四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE= ,则CE的长为 .15. 如图,在矩形ABCD中,AB= ,E是BC的中点,AE⊥BD于点F,则CF的长是 .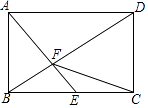 16. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=120°,AD=2,BD平分∠ABC,则梯形ABCD的周长是 .
16. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,∠A=120°,AD=2,BD平分∠ABC,则梯形ABCD的周长是 . 17. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .
17. 在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是 .三、解答题
-
18. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
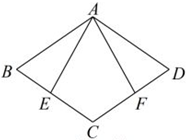 19. 已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断
19. 已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
(1)、构造一个真命题,画图并给出证明;
(2)、构造一个假命题,举反例加以说明.20.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
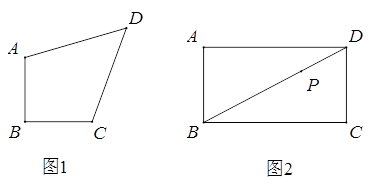 (1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
(1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)、如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.21.已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
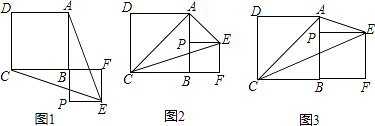
(Ⅰ)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(Ⅱ)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(Ⅲ)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
四、作图题
-
22. 如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
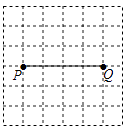 (1)、在图1中画出一个面积最小的¨PAQB.(2)、在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
(1)、在图1中画出一个面积最小的¨PAQB.(2)、在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.五、综合题
-
23. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
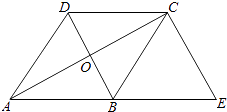 (1)、求证:BD=EC;(2)、若∠E=50°,求∠BAO的大小.24. 如图,在平行四边形 中, ,点 是 的中点,连接 并延长,交 的延长线于点 ,连接 .
(1)、求证:BD=EC;(2)、若∠E=50°,求∠BAO的大小.24. 如图,在平行四边形 中, ,点 是 的中点,连接 并延长,交 的延长线于点 ,连接 .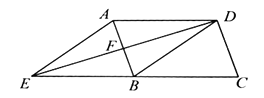 (1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积.25. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)、求证:四边形 是菱形;(2)、若 , ,求菱形 的面积.25. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.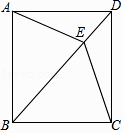 (1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.26. 如图,在矩形 中,线段 、 分别平行于 、 ,它们相交于点 ,点 、 分别在线段 、 上, , ,连接 、 , 与 交于点 .已知 .设 , .
(1)、求证:四边形ABCD是菱形;(2)、如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.26. 如图,在矩形 中,线段 、 分别平行于 、 ,它们相交于点 ,点 、 分别在线段 、 上, , ,连接 、 , 与 交于点 .已知 .设 , .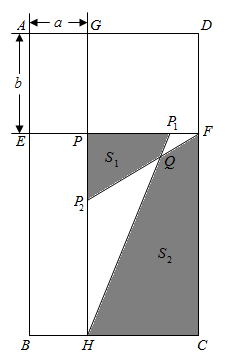 (1)、四边形 的面积四边形 的面积(填“ ”、“ ”或“ ”);(2)、求证: ;(3)、设四边形 的面积为 ,四边形 的面积为 ,求 的值.27.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ;
(1)、四边形 的面积四边形 的面积(填“ ”、“ ”或“ ”);(2)、求证: ;(3)、设四边形 的面积为 ,四边形 的面积为 ,求 的值.27.(1)、如图1,点P为矩形 对角线 上一点,过点P作 ,分别交 、 于点E、F.若 , , 的面积为 , 的面积为 ,则 ; (2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(2)、如图2,点 为 内一点(点 不在 上),点 、 、 、 分别为各边的中点.设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示); (3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示);
(3)、如图3,点 为 内一点(点 不在 上)过点 作 , ,与各边分别相交于点 、 、 、 .设四边形 的面积为 ,四边形 的面积为 (其中 ),求 的面积(用含 、 的代数式表示); (4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可).
(4)、如图4,点 、 、 、 把 四等分.请你在圆内选一点 (点 不在 、 上),设 、 、 围成的封闭图形的面积为 , 、 、 围成的封闭图形的面积为 , 的面积为 , 的面积为 .根据你选的点 的位置,直接写出一个含有 、 、 、 的等式(写出一种情况即可). 28. 问题呈现:
28. 问题呈现:(Ⅰ)如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD . (S表示面积)
(Ⅱ)实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1 , 得到矩形A1B1C1D1 .
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+S .
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与S 之间的数量关系,并说明理由.
(Ⅲ)迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
⑴如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF= ,求EG的长.

⑵如图5,在矩形ABCD中,AB=3,AD=5,点E、H分别在边AB、AD上,BE=1,DH=2,点F、G分别是边BC、CD上的动点,且FG= ,连接EF、HG,请直接写出四边形EFGH面积的最大值.
 29. 综合题
29. 综合题 (1)、【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.30. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)、【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .(2)、【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)(3)、【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.(4)、【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.30. 如图,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC. (1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.31. 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)、求证:四边形BECD是平行四边形;(2)、若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.31. 如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s). (1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.32. 如图
(1)、若m=6,求当P,E,B三点在同一直线上时对应的t的值.(2)、已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.32. 如图 (1)、如图1,菱形 的顶点 、 在菱形 的边上,且 ,请直接写出 的结果(不必写计算过程)(2)、将图1中的菱形 绕点 旋转一定角度,如图2,求 ;(3)、把图2中的菱形都换成矩形,如图3,且 ,此时 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.33. 如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)、如图1,菱形 的顶点 、 在菱形 的边上,且 ,请直接写出 的结果(不必写计算过程)(2)、将图1中的菱形 绕点 旋转一定角度,如图2,求 ;(3)、把图2中的菱形都换成矩形,如图3,且 ,此时 的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.33. 如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF. (1)、求证:四边形BFEP为菱形;(2)、当点E在AD边上移动时,折痕的端点P、Q也随之移动;
(1)、求证:四边形BFEP为菱形;(2)、当点E在AD边上移动时,折痕的端点P、Q也随之移动;①当点Q与点C重合时(如图2),求菱形BFEP的边长;
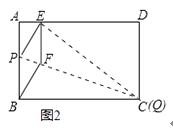
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
34. 如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.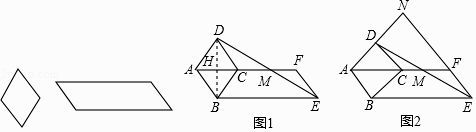 (1)、在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
(1)、在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)、如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求 的值;(3)、在(2)的条件下,若 =k(k为大于 的常数),直接用含k的代数式表示 的值.35. 如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.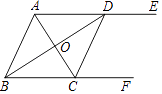 (1)、求证:四边形ABCD是菱形;(2)、若∠ADB=30°,BD=6,求AD的长.36. 如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)、求证:四边形ABCD是菱形;(2)、若∠ADB=30°,BD=6,求AD的长.36. 如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF. (1)、填空:点B的坐标为;(2)、是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)、①求证: = ;
(1)、填空:点B的坐标为;(2)、是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)、①求证: = ;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
37. 如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角. (1)、求证:AD⊥BF;(2)、若BF=BC,求∠ADC的度数.38. 如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.
(1)、求证:AD⊥BF;(2)、若BF=BC,求∠ADC的度数.38. 如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.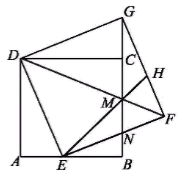 (1)、求证:CD⊥CG;(2)、若tan∠MEN= ,求 的值;(3)、已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为 ?请说明理由.
(1)、求证:CD⊥CG;(2)、若tan∠MEN= ,求 的值;(3)、已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为 ?请说明理由.
-