全国历年中考数学真题精选汇编:四边形1
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、182. 如图,将 绕边 的中点O顺时针旋转180°.嘉淇发现,旋转后的 与 构成平行四边形,并推理如下:
点A,C分别转到了点C,A处,
而点B转到了点D处.
∵ ,
∴四边形 是平行四边形.
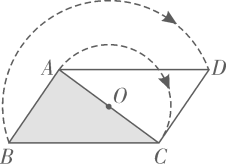
小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是( )
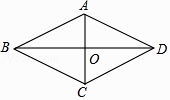
A、嘉淇推理严谨,不必补充 B、应补充:且 , C、应补充:且 D、应补充:且 ,3. 求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )
 A、③→②→①→④ B、③→④→①→② C、①→②→④→③ D、①→④→③→②4. 如图,矩形 的对角线 、 相交于点 , ,过点 作 ,过点 作 , 、 交于点 ,连接 ,则 ( )
A、③→②→①→④ B、③→④→①→② C、①→②→④→③ D、①→④→③→②4. 如图,矩形 的对角线 、 相交于点 , ,过点 作 ,过点 作 , 、 交于点 ,连接 ,则 ( )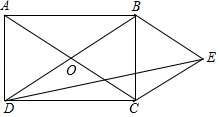 A、 B、 C、 D、5. 下列说法中不正确的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等6. 下列选项中,不能判定四边形ABCD是平行四边形的是
A、 B、 C、 D、5. 下列说法中不正确的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等6. 下列选项中,不能判定四边形ABCD是平行四边形的是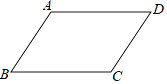 A、 , B、 , C、 , D、 ,7. 在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )A、22 B、20 C、22或20 D、188. 下列命题中,假命题是( )A、矩形的对角线相等 B、矩形对角线交点到四个顶点的距离相等 C、矩形的对角线互相平分 D、矩形对角线交点到四条边的距离相等9. 已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB10. 已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设 = , = ,那么向量 用向量 、 表示为( )A、 + B、 ﹣ C、﹣ + D、﹣ ﹣11. 下列结论中,矩形具有而菱形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直12. 如图,三角板的直角顶点落在矩形纸片的一边上,若∠1=35°,则∠2的度数是( )。
A、 , B、 , C、 , D、 ,7. 在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )A、22 B、20 C、22或20 D、188. 下列命题中,假命题是( )A、矩形的对角线相等 B、矩形对角线交点到四个顶点的距离相等 C、矩形的对角线互相平分 D、矩形对角线交点到四条边的距离相等9. 已知平行四边形ABCD,AC、BD是它的两条对角线,那么下列条件中,能判断这个平行四边形为矩形的是( )A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB10. 已知在△ABC中,AB=AC,AD是角平分线,点D在边BC上,设 = , = ,那么向量 用向量 、 表示为( )A、 + B、 ﹣ C、﹣ + D、﹣ ﹣11. 下列结论中,矩形具有而菱形不一定具有的性质是( )A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直12. 如图,三角板的直角顶点落在矩形纸片的一边上,若∠1=35°,则∠2的度数是( )。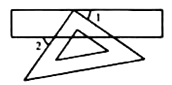 A、35° B、45° C、55° D、65°13. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( )
A、35° B、45° C、55° D、65°13. 如图,在 中, , , ,点D,E,F分别是AB,BC,CA的中点,连结DE,EF,则四边形ADEF的周长为( ) A、6 B、9 C、12 D、1514. 下是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )A、由②推出③,由③推出① B、由①推出②,由②推出③ C、由③推出①,由①推出② D、由①推出③,由③推出②15. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A、6 B、9 C、12 D、1514. 下是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )A、由②推出③,由③推出① B、由①推出②,由②推出③ C、由③推出①,由①推出② D、由①推出③,由③推出②15. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )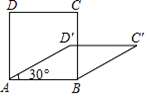 A、1 B、 C、 D、16. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )
A、1 B、 C、 D、16. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为( )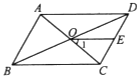 A、50° B、40° C、30° D、20°17. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 , ,则该矩形的面积为( )
A、50° B、40° C、30° D、20°17. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 , ,则该矩形的面积为( ) A、20 B、24 C、 D、
A、20 B、24 C、 D、二、填空题
-
18. 在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是 .19. 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为m.
 20. 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为 cm.
20. 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为 cm. 21. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .
21. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .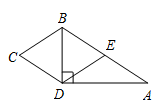 22. 如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件 , 使四边形ABCD是平行四边形(填一个即可).
22. 如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件 , 使四边形ABCD是平行四边形(填一个即可).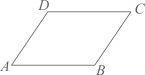 23. 如图,在四边形 中,连接 , .请你添加一个条件 , 使 .(填一种情况即可)
23. 如图,在四边形 中,连接 , .请你添加一个条件 , 使 .(填一种情况即可)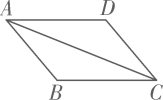 24. 如图,AC、BD是平行四边形ABCD的对角线,设 = , = ,那么向量 用向量 表示为 .
24. 如图,AC、BD是平行四边形ABCD的对角线,设 = , = ,那么向量 用向量 表示为 .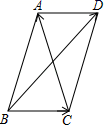 25. 通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是度.26. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)
25. 通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是度.26. 如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为.(结果保留根号)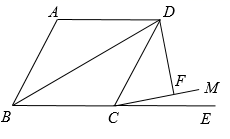 27. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .
27. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .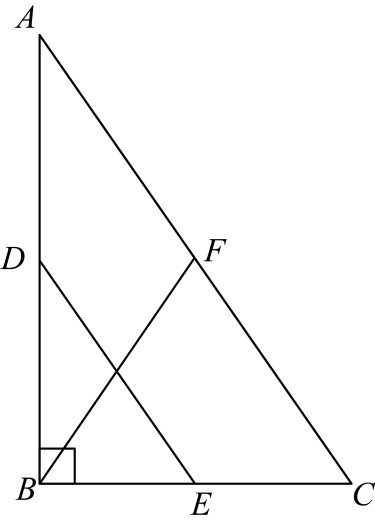 28. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=.
28. 如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=. 29. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。
29. 如图, ABCD的对角线AC,BD相交于点O,请添加一个条件: , 使 ABCD是菱形。 30. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是°.
30. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是°.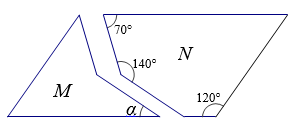
三、解答题
-
31. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.

证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
四、综合题
-
32. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 .
 (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
33. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.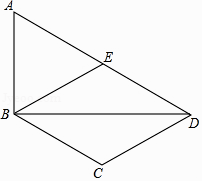 (1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.34. 已知n边形的内角和θ=(n-2)×180°.(1)、甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)、若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.35. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图:
(1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.34. 已知n边形的内角和θ=(n-2)×180°.(1)、甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;(2)、若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.35. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图: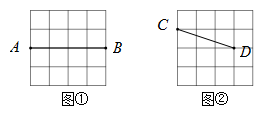 (1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .36. 如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .36. 如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.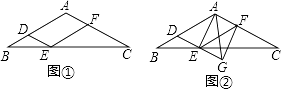 (1)、求证:四边形ADEF为平行四边形;
(1)、求证:四边形ADEF为平行四边形;
(2)、当点D为AB中点时,▱ADEF的形状为;(3)、延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
37. 如图,在 中, 的角平分线交 于点D, .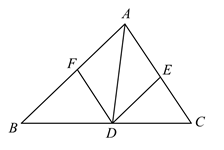 (1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.38. 如图,点C是 的中点,四边形 是平行四边形.
(1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.38. 如图,点C是 的中点,四边形 是平行四边形.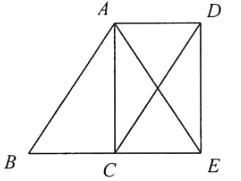 (1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.
(1)、求证:四边形 是平行四边形;(2)、如果 ,求证:四边形 是矩形.
-

