全国历年中考数学真题精选汇编:三角形2
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. △BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
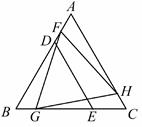 A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长2. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长2. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )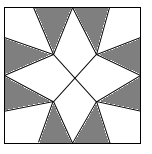 A、 :1 B、3:2 C、 :1 D、 :23. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、 :1 B、3:2 C、 :1 D、 :23. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、54. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )
A、2 B、3 C、4 D、54. 如图,在菱形ABCD中,AB=2,∠A=120°,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H.则四边形EFGH的周长为( )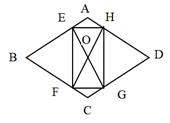 A、 B、 C、 D、5. 如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
A、 B、 C、 D、5. 如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )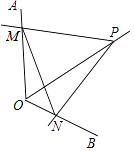 A、4 B、3 C、2 D、16.
A、4 B、3 C、2 D、16.如图,AD是△ABC的角平分线,则AB:AC等于( )
 A、BD:CD B、AD:CD C、BC:AD D、BC:AC7. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、BD:CD B、AD:CD C、BC:AD D、BC:AC7. 如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ) A、4 B、5 C、6 D、78. 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( )
A、4 B、5 C、6 D、78. 如图四边形ABCD中,AD∥BC,∠BCD=90°,AB=BC+AD,∠DAC=45°,E为CD上一点,且∠BAE=45°.若CD=4,则△ABE的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
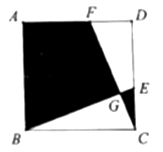
9. 如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .
 10. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .
10. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .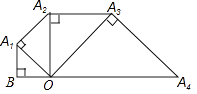 11. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .
11. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .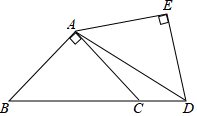 12. 如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP=.
12. 如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP=. 13. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)
13. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)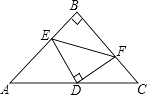 14. 如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为 .
14. 如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为 .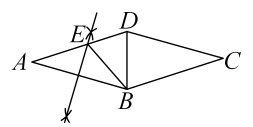 15. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .
15. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .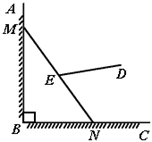 16. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且 ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;② 的周长为 ;③ ;④ 的面积的最大值 .其中正确的结论是.(填写所有正确结论的序号)
16. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且 ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;② 的周长为 ;③ ;④ 的面积的最大值 .其中正确的结论是.(填写所有正确结论的序号)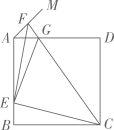 17.
17.如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 , 现有如下结论:
①S1:S2=AC2:BC2;
②连接AE,BD,则△BCD≌△ECA;
③若AC⊥BC,则S1•S2= S32 .
其中结论正确的序号是 .
 18. 如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.
18. 如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.
当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2 , 易知∠1=∠2.若A1A2⊥AO , 光线又会沿A2→A1→A原路返回到点A,此时∠A=°.
若光线从点A发出后,经若干次反射能沿原路返回到点A , 则锐角∠A的最小值=°.
三、解答题
-
19.
已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
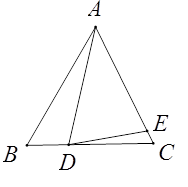 (1)、如图,若点D在线段BC上,点E在线段AC上.
(1)、如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)、是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.20.问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
 (1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)、△DEF是否为正三角形?请说明理由;(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系。21. 如图,在正方形 中, 是 边上一点,(与 、 不重合),连接 ,将 沿 所在的直线折叠得到 ,延长 交 于 ,连接 ,作 ,与 的延长线交于点 ,连接 .显然 是 的平分线, 是 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于 的角平分线),并说明理由.
(1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)、△DEF是否为正三角形?请说明理由;(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系。21. 如图,在正方形 中, 是 边上一点,(与 、 不重合),连接 ,将 沿 所在的直线折叠得到 ,延长 交 于 ,连接 ,作 ,与 的延长线交于点 ,连接 .显然 是 的平分线, 是 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于 的角平分线),并说明理由.
四、综合题
-
22. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形
 (1)、已知凸五边形ABCDE的各条边都相等
(1)、已知凸五边形ABCDE的各条边都相等①如图1,若AC=AD=BE=BD=CE,求证:五边形ABCDE是正五边形
②2如图2,若AC=BE=CE,请判断五边形ABCDE是不是正五边形,并说明理由
(2)、判断下列命题的真假,(在括号内填写“真”或“假”),如图3,已知凸六边形ABCDEF的各条边都相等①若AC=CE=EA,则六边形ABCDEF是正六边形()
②若AD=BE=CF,则六边形ABCDEF是正六边形()
23.如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴上的一动点,连接CD,DE,以CD,DE为边作▱CDEF.
 (1)、当0<m<8时,求CE的长(用含m的代数式表示);(2)、当m=3时,是否存在点D,使▱CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;(3)、点D在整个运动过程中,若存在唯一的位置,使得▱CDEF为矩形,请求出所有满足条件的m的值.24.
(1)、当0<m<8时,求CE的长(用含m的代数式表示);(2)、当m=3时,是否存在点D,使▱CDEF的顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;(3)、点D在整个运动过程中,若存在唯一的位置,使得▱CDEF为矩形,请求出所有满足条件的m的值.24.如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
 (1)、请用直尺和圆规画一个“好玩三角形”;(2)、如图在Rt△ABC中,∠C=90°,tanA= ,求证:△ABC是“好玩三角形”;(3)、如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
(1)、请用直尺和圆规画一个“好玩三角形”;(2)、如图在Rt△ABC中,∠C=90°,tanA= ,求证:△ABC是“好玩三角形”;(3)、如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.①当β=45°时,若△APQ是“好玩三角形”,试求 的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)、(本小题为选做题)依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
25.若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
 (1)、如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)、如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)、四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.26.
(1)、如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)、如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)、四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.26.一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
 (1)、
(1)、理清思路完成解答
本题证明的思路可用下列框图表示:

根据上述思路,请你完整地书写本题的证明过程.
(2)、若PB平分∠ABO,其余条件不变.求证:AP=CD.(3)、知识迁移,探索新知若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
27. 【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.

【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)、如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 , 可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)、如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)、在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)(4)、∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 , 则△ABC≌△DEF.28. 在 中, , , 于点 .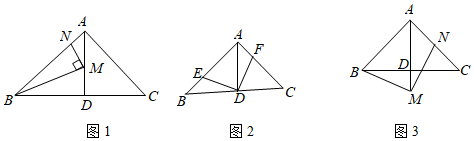 (1)、如图1,点 , 分别在 , 上,且 ,当 , 时,求线段 的长;(2)、如图2,点 , 分别在 , 上,且 ,求证: ;(3)、如图3,点 在 的延长线上,点 在 上,且 ,求证: .29. 问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC= AB.
(1)、如图1,点 , 分别在 , 上,且 ,当 , 时,求线段 的长;(2)、如图2,点 , 分别在 , 上,且 ,求证: ;(3)、如图3,点 在 的延长线上,点 在 上,且 ,求证: .29. 问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC= AB.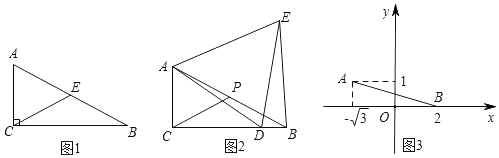
探究结论:小明同学对以上结论作了进一步研究.
(1)、如图1,连接AB边上中线CE,由于CE= AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .(2)、如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.(3)、当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论.拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣ ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
30.(1)、如图1,△ABC为等边三角形,现将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°),旋转后三角板的一直角边与AB交于点D,在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
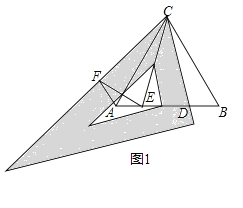
①求∠EAF的度数;
②DE与EF相等吗?请说明理由;
(2)、如图2,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°),旋转后三角板的一直角边与AB交于点D,在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF,请直接写出探究结果:
①求∠EAF的度数;
②线段AE,ED,DB之间的数量关系.
 31.
31.边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2
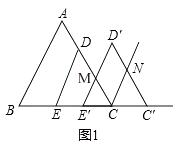 (1)、如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.(2)、
(1)、如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.(2)、如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
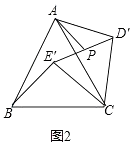
32.数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究:
 (1)、小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)、小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.33.
(1)、小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)、小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.33.按要求回答问题:
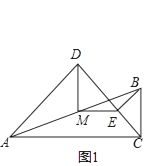
 (1)、已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;(2)、若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;(3)、若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)34. 在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.(1)、
(1)、已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;(2)、若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;(3)、若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)34. 在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.(1)、如图1,当∠ADC=90°时,线段MD与ME的数量关系是;
 (2)、
(2)、如图2,当∠ADC=60°时,试探究线段MD与ME的数量关系,并证明你的结论;
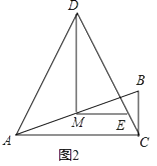 (3)、
(3)、如图3,当∠ADC=α时,求 的值.
 35. 如图,在Rt ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
35. 如图,在Rt ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).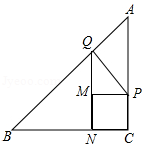 (1)、当t为何值时,点B在线段PQ的垂直平分线上?(2)、是否存在某一时刻t,使 APQ是以PQ为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;(3)、以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.36.
(1)、当t为何值时,点B在线段PQ的垂直平分线上?(2)、是否存在某一时刻t,使 APQ是以PQ为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;(3)、以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.36.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
 (1)、当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)、在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)、是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.37.
(1)、当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)、在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)、是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.37.如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE;过点F作FG⊥BC交BC的延长线于点G.
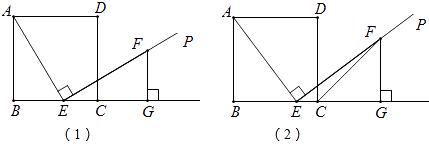 (1)、求证:FG=BE;(2)、连接CF,如图(2),求证:CF平分∠DCG;(3)、当 = 时,求sin∠CFE的值.38. 在等边 中, , ,垂足为D,点E为AB边上一点,点F为直线BD上一点,连接EF.
(1)、求证:FG=BE;(2)、连接CF,如图(2),求证:CF平分∠DCG;(3)、当 = 时,求sin∠CFE的值.38. 在等边 中, , ,垂足为D,点E为AB边上一点,点F为直线BD上一点,连接EF. (1)、将线段EF绕点E逆时针旋转60°得到线段EG,连接FG.
(1)、将线段EF绕点E逆时针旋转60°得到线段EG,连接FG.①如图1,当点E与点B重合,且GF的延长线过点C时,连接DG,求线段DG的长;
②如图2,点E不与点A,B重合,GF的延长线交BC边于点H,连接EH,求证: ;
(2)、如图3,当点E为AB中点时,点M为BE中点,点N在边AC上,且 ,点F从BD中点Q沿射线QD运动,将线段EF绕点E顺时针旋转60°得到线段EP,连接FP,当 最小时,直接写出 的面积.39. 在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.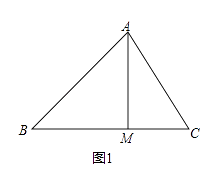
 (1)、如图1,若AB=3 ,BC=5,求AC的长;(2)、如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
(1)、如图1,若AB=3 ,BC=5,求AC的长;(2)、如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.