全国历年中考数学真题精选汇编:三角形1
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 下列长度的三条线段与长度为5的线段能组成四边形的是( )A、1,1,1 B、1,1,8 C、1,2,2 D、2,2,22. 折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )A、 B、2 C、 D、43. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )
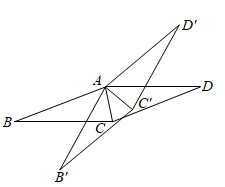 A、 B、 C、 D、4. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、 B、 C、 D、4. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )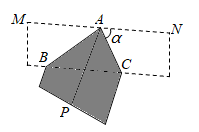 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm25. 两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M,若BC∥EF,则∠BMD的大小为( )
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm25. 两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M,若BC∥EF,则∠BMD的大小为( )
 A、60° B、67.5° C、75° D、82.5°6. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、60° B、67.5° C、75° D、82.5°6. 如图, 中, ,点D在 上, .若 ,则 的长度为( )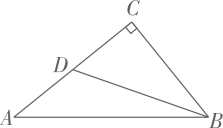 A、 B、 C、 D、47. 如图,直线m∥n , 三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若∠1=60°,则下列结论错误的是( )
A、 B、 C、 D、47. 如图,直线m∥n , 三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若∠1=60°,则下列结论错误的是( )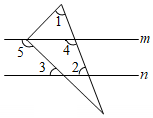 A、∠2=75° B、∠3=45° C、∠4=105° D、∠5=130°8. 如图,在平行四边形ABCD中,E是BD的中点,则下列四个结论:
A、∠2=75° B、∠3=45° C、∠4=105° D、∠5=130°8. 如图,在平行四边形ABCD中,E是BD的中点,则下列四个结论:①AM=CN;②若MD=AM , ∠A=90°,则BM=CM;③若MD=2AM , 则S△MNC=S△BNE;④若AB=MN , 则△MFN与△DFC全等.
其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个9. 如图,在矩形ABCD中,AB=5,BC=5 ,点P在线段BC上运动(含B、C两点),连接AP , 以点A为中心,将线段AP逆时针旋转60°到AQ , 连接DQ , 则线段DQ的最小值为( )
A、1个 B、2个 C、3个 D、4个9. 如图,在矩形ABCD中,AB=5,BC=5 ,点P在线段BC上运动(含B、C两点),连接AP , 以点A为中心,将线段AP逆时针旋转60°到AQ , 连接DQ , 则线段DQ的最小值为( )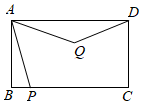 A、 B、 C、 D、310. 如图,在四边形ABCD中, , , , .分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )
A、 B、 C、 D、310. 如图,在四边形ABCD中, , , , .分别以点A,C为圆心,大于 长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为( )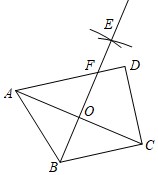 A、 B、4 C、3 D、11. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、 B、4 C、3 D、11. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )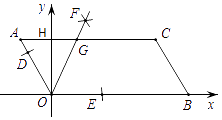 A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)12. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)12. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )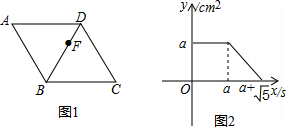 A、 B、2 C、 D、213. 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )
A、 B、2 C、 D、213. 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )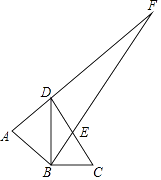 A、30° B、15° C、45° D、25°
A、30° B、15° C、45° D、25°二、填空题
-
14. 如图,在边长为6的等边 中,点 , 分别是边 , 上的动点,且 ,连接 , 交于点 ,连接 ,则 的最小值为.
 15. 如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在 上,边AB、AC分别交 于D、E两点﹐点B是 的中点,则∠ABE=.
15. 如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在 上,边AB、AC分别交 于D、E两点﹐点B是 的中点,则∠ABE=.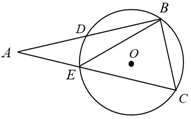 16. 《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为尺.
16. 《九章算术》中有一道“引葭赴岸”问题:“仅有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(示意图如图,则水深为尺. 17. 如图,在正五边形ABCDE中,连结AC,BD交于点F,则 的度数为.
17. 如图,在正五边形ABCDE中,连结AC,BD交于点F,则 的度数为.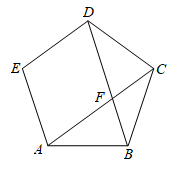 18. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , .
18. 图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且 ,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得 , , . (1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )19. 如图,在△ABC中,∠ACB=90°,AC<BC.分别以点A,B为圆心,大于 AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.若BC=3,则△AFH的周长为 .
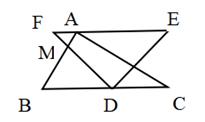
(1)、椅面CE的长度为cm.(2)、如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角 的度数达到最小值 时,A,B两点间的距离为cm(结果精确到0.1cm).(参考数据: , , )19. 如图,在△ABC中,∠ACB=90°,AC<BC.分别以点A,B为圆心,大于 AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF为半径画弧,交BC延长线于点H,连接AH.若BC=3,则△AFH的周长为 .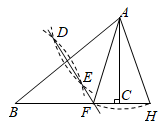 20. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究:
20. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究: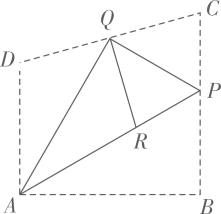 (1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .21. 如图,在 中, , , 分别为 、 的中点, ,过点 作 ,交 的延长线于点 ,则四边形 的面积为 .
(1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .21. 如图,在 中, , , 分别为 、 的中点, ,过点 作 ,交 的延长线于点 ,则四边形 的面积为 .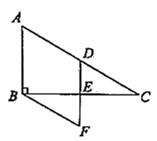 22. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE , 若DE=EF , CE=2,则AD的长为 .
22. 如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE , 若DE=EF , CE=2,则AD的长为 .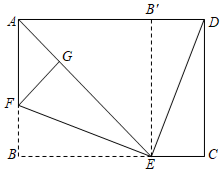 23. 如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为 .
23. 如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为 .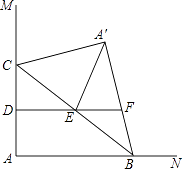
三、计算题
-
24. 化简求值: ,其中 与2,3构成三角形的三边,且 为整数.
四、解答题
-
25. 在①AE=CF;②OE=OF;③BE∥DF这三个条件中任选一个补充在下面横线上,并完成证明过程.

已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上, (填写序号).
求证:BE=DF.(注:如果选择多个条件分别解答,按第一个解答计分.)
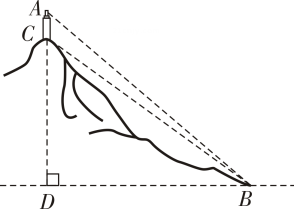
26. 如图,山顶上有一个信号塔 ,已知信号塔高 米,在山脚下点B处测得塔底C的仰角 ,塔顶A的仰角 .求山高 (点 在同一条竖直线上).(参考数据: )
 27. 如图,在菱形 中,点 、 分别在 、 上,且 ,求证: .
27. 如图,在菱形 中,点 、 分别在 、 上,且 ,求证: .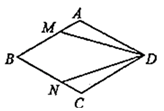
五、综合题
-
28. 如图,在平面直角坐标中, 的顶点坐标分别是 , , .
 (1)、将 以 为旋转中心旋转 ,画出旋转后对应的 ;(2)、将 平移后得到 ,若点 的对应点 的坐标为 ,求 的面积29. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
(1)、将 以 为旋转中心旋转 ,画出旋转后对应的 ;(2)、将 平移后得到 ,若点 的对应点 的坐标为 ,求 的面积29. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.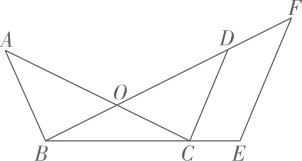 (1)、求证 ;(2)、若 ,求 的长.30. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.
(1)、求证 ;(2)、若 ,求 的长.30. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.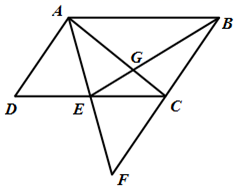 (1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.31. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF.
(1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.31. 如图,在 中, ,BC与 相切于点D,过点A作AC的垂线交CB的延长线于点E,交 于点F,连结BF. (1)、求证:BF是 的切线.(2)、若 , ,求EF的长.32. 如图,在四边形ABCD中,AB=AD=20,BC=DC=10 .
(1)、求证:BF是 的切线.(2)、若 , ,求EF的长.32. 如图,在四边形ABCD中,AB=AD=20,BC=DC=10 .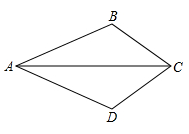 (1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.33. 如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E。已知∠ABC=60°,∠C=45°。
(1)、求证:△ABC≌△ADC;(2)、当∠BCA=45°时,求∠BAD的度数.33. 如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E。已知∠ABC=60°,∠C=45°。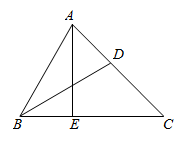 (1)、求证:AB=BD;(2)、若AE=3,求△ABC的面积。34. 如图1.已知四边形 是矩形.点E在 的延长线上. 与 相交于点G,与 相交于点(1)、求证: ;(2)、若 ,求 的长;
(1)、求证:AB=BD;(2)、若AE=3,求△ABC的面积。34. 如图1.已知四边形 是矩形.点E在 的延长线上. 与 相交于点G,与 相交于点(1)、求证: ;(2)、若 ,求 的长;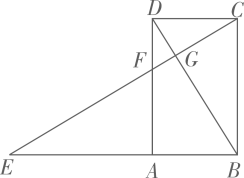 (3)、如图2,连接 ,求证: .
(3)、如图2,连接 ,求证: . 35. 如图,在边长为1个单位长度的小正方形组成的12×12的网格中,给出了以格点(网格线的交点)为端点的线段A
35. 如图,在边长为1个单位长度的小正方形组成的12×12的网格中,给出了以格点(网格线的交点)为端点的线段AB.
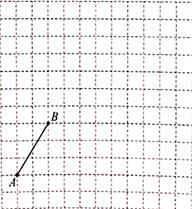 (1)、将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段C
(1)、将线段AB向右平移5个单位,再向上平移3个单位得到线段CD,请画出线段CD.
(2)、以线段CD为一边,作一个菱形CDEF,且点E,F也为格点.(作出一个菱形即可)36. 如图,点E在▱ABCD内部,AF∥BE,DF∥CE.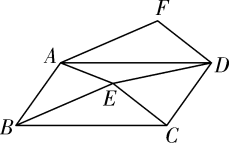 (1)、求证:△BCE≌△ADF;(2)、设▱ABCD的面积为S,四边形AEDF的面积为T,求 的值37. 四边形ABCD为矩形,E是AB延长线上的一点.
(1)、求证:△BCE≌△ADF;(2)、设▱ABCD的面积为S,四边形AEDF的面积为T,求 的值37. 四边形ABCD为矩形,E是AB延长线上的一点.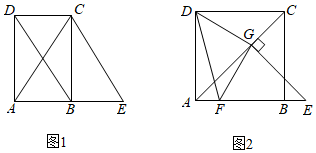 (1)、若AC=EC , 如图1,求证:四边形BECD为平行四边形;(2)、若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.38. 如图,在直角坐标系中,直线y1=ax+b与双曲线y2= (k≠0)分别相交于第二、四象限内的A(m,4),B(6,n)两点,与x轴相交于C点.已知OC=3,tan∠ACO= .
(1)、若AC=EC , 如图1,求证:四边形BECD为平行四边形;(2)、若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.38. 如图,在直角坐标系中,直线y1=ax+b与双曲线y2= (k≠0)分别相交于第二、四象限内的A(m,4),B(6,n)两点,与x轴相交于C点.已知OC=3,tan∠ACO= .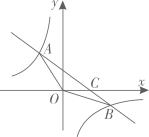 (1)、求y1 , y2对应的函数表达式;(2)、求△AOB的面积;(3)、直接写出当x<0时,不等式ax+b> 的解集.39. 如图
(1)、求y1 , y2对应的函数表达式;(2)、求△AOB的面积;(3)、直接写出当x<0时,不等式ax+b> 的解集.39. 如图 (1)、问题发现
(1)、问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
① 的值为;
②∠AMB的度数为 .
(2)、类比探究如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数,并说明理由;
(3)、拓展延伸在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB= ,请直接写出当点C与点M重合时AC的长.
40. (1)、问题发现
(1)、问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①∠AEB的度数为;
②线段AD,BE之间的数量关系为 .
(2)、拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)、解决问题如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
-