全国历年中考数学真题精选汇编:相交线与平行线
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
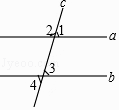 A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠42. 已知 ,直线EF分别交AB、CD于点G、H,∠EGB=25°,将一个60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于( )
A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠42. 已知 ,直线EF分别交AB、CD于点G、H,∠EGB=25°,将一个60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于( )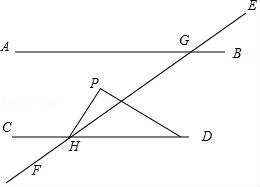 A、30° B、35° C、40° D、45°3. 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A、30° B、35° C、40° D、45°3. 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )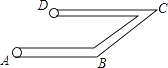 A、AB∥BC B、BC∥CD C、AB∥DC D、AB与CD相交4. 如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点G,则∠GEB的度数为( )
A、AB∥BC B、BC∥CD C、AB∥DC D、AB与CD相交4. 如图,AB∥CD,∠EFD=64°,∠FEB的角平分线EG交CD于点G,则∠GEB的度数为( ) A、66° B、56° C、68° D、58°5. 如图,直线 ,且 于点 ,若 ,则 的度数为( )
A、66° B、56° C、68° D、58°5. 如图,直线 ,且 于点 ,若 ,则 的度数为( )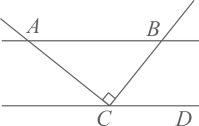 A、65° B、55° C、45° D、35°6. 如图,AC与BD交于点O,AB∥CD,∠AOB=105°,∠B=30°,则∠C的度数为( )
A、65° B、55° C、45° D、35°6. 如图,AC与BD交于点O,AB∥CD,∠AOB=105°,∠B=30°,则∠C的度数为( )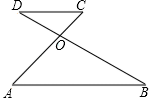 A、45° B、55° C、60° D、75°7. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )
A、45° B、55° C、60° D、75°7. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )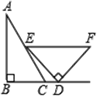 A、 B、 C、 D、8. 如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )
A、 B、 C、 D、8. 如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( ) A、50° B、55° C、60° D、65°9. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A、50° B、55° C、60° D、65°9. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )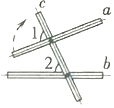 A、10° B、20° C、50° D、70°10. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是( )
A、10° B、20° C、50° D、70°10. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是( )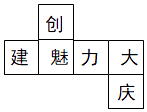 A、庆 B、力 C、大 D、魅11. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
A、庆 B、力 C、大 D、魅11. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )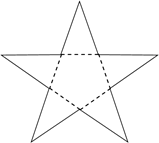 A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱12. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱12. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )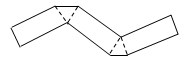 A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥13. 如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥13. 如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( ) A、36° B、34° C、32° D、30°14. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )
A、36° B、34° C、32° D、30°14. 将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是( )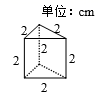 A、
A、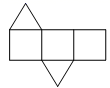 B、
B、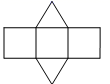 C、
C、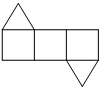 D、
D、 15. 将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( )
15. 将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( )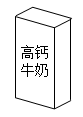 A、
A、 B、
B、 C、
C、 D、
D、 16. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )
16. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )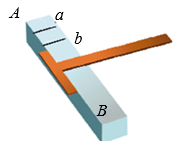 A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行17. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行17. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )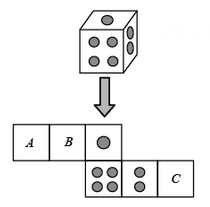 A、 代表
A、 代表 B、 代表
B、 代表  C、 代表
C、 代表  D、 代表
D、 代表  18. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
18. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )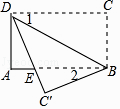 A、20° B、30° C、35° D、55°19. 如图,将一副三角尺按下列位置摆放,使 和 互余的摆放方式是( )A、
A、20° B、30° C、35° D、55°19. 如图,将一副三角尺按下列位置摆放,使 和 互余的摆放方式是( )A、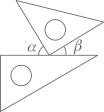 B、
B、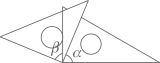 C、
C、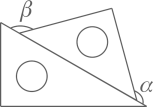 D、
D、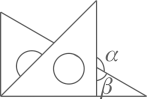 20. 直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
20. 直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )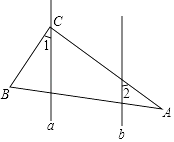 A、65° B、50° C、55° D、60°21. 如图,点C在∠AOB的边OA上,用尺规作出了CP∥OB,作图痕迹中, 是( )
A、65° B、50° C、55° D、60°21. 如图,点C在∠AOB的边OA上,用尺规作出了CP∥OB,作图痕迹中, 是( ) A、以点C为圆心、OD的长为半径的弧 B、以点C为圆心、DM的长为半径的弧 C、以点E为圆心、DM的长为半径的弧 D、以点E为圆心、OD的长为半径的弧22. 把 与 放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若 , ,则 的度数是( )
A、以点C为圆心、OD的长为半径的弧 B、以点C为圆心、DM的长为半径的弧 C、以点E为圆心、DM的长为半径的弧 D、以点E为圆心、OD的长为半径的弧22. 把 与 放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若 , ,则 的度数是( ) A、 B、57° C、 D、23. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )
A、 B、57° C、 D、23. 曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光。如图, 两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( ) A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线24. 如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上,若∠1=20°,则∠2的度数为( )
A、两点之间,线段最短 B、平行于同一条直线的两条直线平行 C、垂线段最短 D、两点确定一条直线24. 如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上,若∠1=20°,则∠2的度数为( ) A、20° B、30° C、40° D、50°25. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )
A、20° B、30° C、40° D、50°25. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )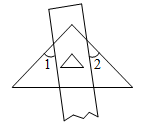 A、40° B、43° C、45° D、47°26. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )
A、40° B、43° C、45° D、47°26. 如图,设点P是直线 外一点,PQ⊥ ,垂足为点Q,点T是直线 上的一个动点,连结PT,则( )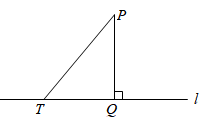 A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ27. 某同学的作业如下框,其中※处填的依据是( )
A、PT≥2PQ B、PT≤2PQ C、PT≥PQ D、PT≤PQ27. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
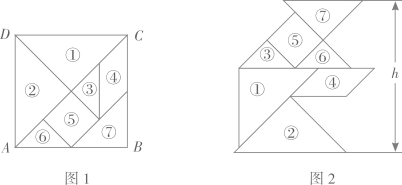
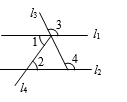 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补28. 七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补28. 七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )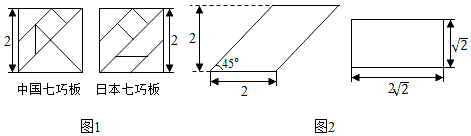 A、1和1 B、1和2 C、2和1 D、2和2
A、1和1 B、1和2 C、2和1 D、2和2二、填空题
-
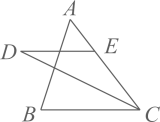
29. 如图,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E.若∠AED=50°,则∠D的度数为.
 30. 如图 , , ,则 °.
30. 如图 , , ,则 °.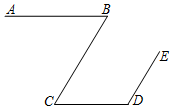 31. 如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
31. 如图,某单位要在河岸 上建一个水泵房引水到C处,他们的做法是:过点C作 于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 . 32. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
32. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .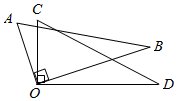 33. 如图,点O在直线 上, ,则 的度数是 .
33. 如图,点O在直线 上, ,则 的度数是 . 34. 如图,CD平分∠ECB,且CD∥AB,若∠A=36°,则∠B= .
34. 如图,CD平分∠ECB,且CD∥AB,若∠A=36°,则∠B= . 35. 如图,直线 , 的顶点 和 分别落在直线 和 上,若 , ,则 的度数是.
35. 如图,直线 , 的顶点 和 分别落在直线 和 上,若 , ,则 的度数是.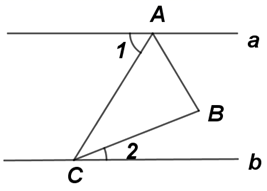 36. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”。已知正方形ABCD的边长为4dm,则图2中h的值为dm。
36. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”。已知正方形ABCD的边长为4dm,则图2中h的值为dm。
三、解答题
-
37.
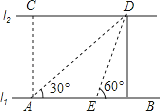
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
四、作图题
-
38. 如图,C为线段 外一点.
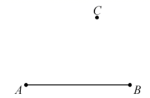 (1)、求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的四边形 中, , 相交于点P, , 的中点分别为 ,求证: 三点在同一条直线上.
(1)、求作四边形 ,使得 ,且 ;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的四边形 中, , 相交于点P, , 的中点分别为 ,求证: 三点在同一条直线上.五、综合题
-
39.
如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.
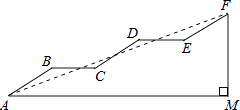 (1)、求FM的长;(2)、连接AF,若sin∠FAM= ,求AM的长.40.
(1)、求FM的长;(2)、连接AF,若sin∠FAM= ,求AM的长.40.用两种方法证明“三角形的外角和等于360°”.如图,
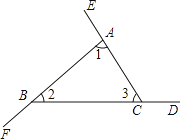
∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
请把证法1补充完整,并用不同的方法完成证法2.
(1)、证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
(2)、证法2
-
-