江西省南昌市2020-2021学年八年级下学期数学期末试卷
试卷更新日期：2021-07-08 类型：期末考试
一、选择题(本大题共6小题，每小题3分，共18分) 在每小题给出的四个选项中，只有一项是正确的，每小题选对得3分，选错、不选或多选均得零分。
-
1. 的相反数是（ ）A、 B、 C、3 D、2. 如图，△OAB为直角三角形，OA=5，AB=4，则点A的坐标为（ ）
A、(4，5) B、(4，3) C、(3，4) D、(3，5)3. 如图，矩形ABCD的对角线AC=8，∠BOC=120°，则AB的长为（ ）
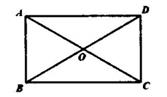A、3 B、4 C、5 D、64. 一次函数y=kx-3(k≠0)的函数值y随x的增人而减小，它的图象不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图，直线y=2x和y=kx+b相交于点P (2，4)，则不等式2x≤kx+b的解集为（ ）
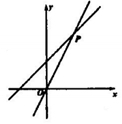A、x≥4 B、x≤4 C、x≥2 D、x≤26. 一组数据：a1 ， a2 ， ……，an ， 的平均数为P，众数为Z，中位数为W，则以下判断正确的是（ ）A、P一定出现在a1 ， a2 ， ……，an中 B、Z一定出现在a1 ， a2 ， ……，an中 C、W一定出现在a1 ， a2 ， ……，an中 D、P，Z，W都不会出现在a1 ， a2 ， ……，an中二、填空题(本大题共6小题，每小题3分，共18分)
-
7. 化简： = ．8. 将函数y=2x的图象向下平移3个单位后的函数解析式是y=9. 如图，点P是正方形ABCD内位于对角线AC下方的一点，已知：∠PCA=∠PBC，则∠BPC的度数为
10. 南吕是国家历史文化名城，其名源于“昌大南疆，南方昌盛”之意，市内的滕王阁、八一起义纪念馆、海昏侯遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴、某班同学分小组到以上五个地方进行研学，人数分别为：12，5，11，5，7 (单位：人)，这组数据的中位数是11. 一组数据3，5，3，x的众数只有一个，则x的值不能为12. 如图，在△ABC中，已知：∠ACB=90°，AB=10cm，AC=6cm，动点P从点B出发，沿射线BC以1cm/s的速度运动，设运动的时间为1秒，连接PA，当△ABP为等腰三角形时，t的值为
三、解答题(本大题共5小题，每小题6分，共30分)
-
13.(1)、计算：(2)、求x的值：14. 如图，点C为线段AB上一点且不与A，B两点重合，分别以AC，BC为边向AB的同侧做锐角为60°的菱形。请仅用无刻度的真尺分别按下列要求作图。(保留作图痕迹)
(1)、在图1中，连接DF，若AC=BC，作出线段DF的中点M；(2)、在图2中，连接DF，若AC≠BC，作出线段DF的中点N。15. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃(读kin，门槛的意思)一尺，不合二寸，问门广儿何？题目大意是：如图1、2 (图2为图1的俯视示意图)，今推开双门，门框上点C和点D到门J槛AB的距离DE为1尺(1尺=10寸)，双门间的缝隙CD为2寸。求门宽AB的长是多少寸？
16. 某种子站销售一种玉米种子，单价为5元千克，为惠民促销，推出以下销售方案：付款金额y (元)与购买种子数量x (千克)之间的函数关系如图所示。
(1)、当x≥2时，求y与x之间的函数关系式：(2)、徐大爷付款20元能购买这种玉米种子多少千克？17. 已知1：①1，2，3，4，5的平均数是3，方差是2；②2，3，4，5，6的平均数是4，方差是2；
③1，3，5，7，9的平均数是5，方差是8；
④2，4，6，8，10的平均数是6，方差是8；
请按要求填空：
(1)、n，n+1，n+2，n+3，n+4的平均数是 ， 方差是；(2)、n，n+2，n+4，n+6，n+8的平均数是 ，方差是；(3)、n，2n，3n，4n，5n的平均数是 ， 方差是。四、解答题(本大题共3小题，每小题8分，共24分)
-
18. 下表是某公司员工月收入的资料。
职位
总经理
财务总监
部门经理
技术人员
前台
保安
保洁
人数
1
1
2
10
2
3
1
月收入/元
40000
30000
6000
5000
43500
3000
2000
(1)、这家公司员工月收入的平均数是7500元，中位数是和众数是(2)、在(1)中的平均数，中位数和众数哪些统计量能反映该公司全体员工收入水平？说明理由；(3)、为了避免技术人员流失，该公司决定给他们每人每月加薪x元至公司员工月收入的平均数，求x的值。19. 已知：一次函数y=mx+(2-m(m#0)与x轴、y轴交于A点，B点。(1)、当m=4时，求△OAB的面积；(2)、请选择你喜欢的两个不同的m(m≠0)的值，求得到的两个一次函数的交点坐标；(3)、m为何值时，△OAB是等腰直角三角形？20. 如图1，岩DE是△ABC的中位线，则S△ABC=4S△ADE ， 解答下列问题：
(1)、如图2，点P是BC边上一点，连接PD、PE①若S△PBD=1，则S△ABC=；
②岩S△PBD=2，S△PCE=3，连接AP，则S△APD= ， S△APE= ， S△ABC=。
(2)、如图3，点P是△ABC外一点，连接PD、PE，已知：S△PBD=4，S△PBD=5，S△PDE=6，求S△ABC的值；(3)、如图4，点P是正六边形FGHIJK内一点，连接PG、PF、PK，已知：S△PGF=7，S△PKJ=8，S△PFK=9，求S六边形FGHIJK的值。
五、综合题(本大题共1小题，共10分)
-
21. 已知直线y=-x+4分别与x轴、y轴交于A点，B点，点Q(xn ， yn)为这条直线上的点，QP⊥x轴于点P，QR⊥y轴于点R。(1)、①将下表中的空格填写完整：
n
1
2
3
4
5
6
7
8
9
xn
-2
-1
0
1
2
3
4
5
6
yn
6
5
4
3
2
1
0
-1
-2
xn+yn
4
4
4
4
4
②根据表格中的数据，下列判断正确的是
A． =
B．
C． =0
(2)、当点Q在第一象限时，解答下列问题：
①求证：矩形OPQR的周长是一个定值，并求这个定值；
②设矩形OPQR的面积为S，求证：S≤4
(3)、当点Q在第四象限时，直接写出QP，QR满足的等式关系。