安徽省宣城市2020-2021学年八年级下学期数学期末试卷
试卷更新日期：2021-07-08 类型：期末考试
一、选择题：(每小题3分，共30分)
-
1. 下列二次根式中，最简二次根式是（ ）A、 B、 C、 D、2. 下列各组数中，以a、b、c为边的三角形不是直角三角形的是（ ）A、a=1、b=2、c= B、a=1.5、b=2、c=3 C、a=6、b=8、c= 10 D、a=3、b=4、c=53. 用配方法解方程3x2-6x-1=0时，方程可变形为（ ）A、(3x-1)2=1 B、3(x-1)2= C、(x-1)2= D、(x-3)2=4. 冉冉的妈妈在网上销售装饰品，最近一周每天销售某种装饰品的个数为：11，10，11，13，11，13，15，关于这组数据冉冉得出如下结果，其中错误的是（ ）A、众数是11 B、中位数是13 C、平均数是12 D、方差是5. 正多边形通过镶嵌能够密铺成一个无缝隙的平面，下列组合中不能镶嵌成一个平面的是（ ）A、正三角形和正方形 B、正三角形和正六边形 C、正方形和正六边形 D、正方形和正八边形6. 下列方程中，没有实数根的是（ ）A、3x2- x+2=0 B、4x2+4x+1=0 C、x2-3x-4=0 D、 x2-x-1=07. 下列说法：①一组对边平行，另一组对边相等的四边形是平行四边形；②对角线互相垂直的四边形是菱形；③四条边相等的四边形是正方形；④顺次连接菱形各边中点形成的四边形一定是矩形。其中正确的个数是（ ）A、4 B、3 C、2 D、18. 下表中记录了甲、乙、丙、丁四名运动员跳远选拔赛成绩(单位：cm)的平均数和方差，要从中选择一名成绩较高且发挥稳定的运动员参加决赛，最合适的运动员是（ ）
甲
乙
丙
丁
平均数
376
350
376
350
方差s2
12.5
13.5
2.4
5.4
A、甲 B、乙 C、丙 D、丁9. 如图为矩形ABCD，一条直线将该矩形分割成两个多边形，若这两个多边形的内角和分别为a和b，则a+b不可能是（ ）
A、360° B、540° C、720° D、900°10. 如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC=12，点P在正方形的边上，则满足PE+PF=9的点P的个数是（ ）
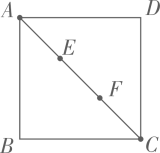A、0 B、4 C、6 D、8二、填空题：(每小题3分，共18分)
-
11. 已知y= + +3，则xy=12. “杂交水稻之父”袁隆平为提高水稻的产量奉献了自己的一生。某村种植了杂交水稻2018年的平均亩产300千克，2020年平均亩产363千克，则此水稻亩产量的平均增长率为13.
在数轴上表示实数a的点如图所示，化简 ＋|a－2|的结果为 ．
14. 已知2+ 是关于x的方程x2-4x+m=0的一个根，则m=。15. 如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长=
16. 如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB=10，MN=3，则AC的长为
三、计算题：(每小题5分，共10分)
-
17. 计算：18. 解方程：2x2-3x-5=0
四、解答题：(共5小题，共42分)
-
19. 精准扶贫是我国扶贫开发工作中的重点工作，某村提倡贫困户在家承接手工产品提高经济收入。张大爷一家承接的手工产品成本每件10元，销售单价为20元时，每月销量为300件，销售价每降低1元，每月销量增加10件。政府根据每月销量补贴每件2元扶贫补助金。(1)、当销售单价定为15元，那么政府本月补助张大爷一 家多少元？(2)、产品每月的销售利润加每月政府补助金是张大爷一家的手工产品收入，当某月销售单价为多少元时，张大爷一家能获得3200元的收入？20. 如图，在4×4的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形。
⑴在图1中，画一个直角三角形，使它的三边长都是有理数；⑵在图2中，画-个直角三角形，使它的一边长是有理数，另外两边长是无理数；
⑶在图3中，画一个直角三角形，使它的三边长都是无理数。
21. 已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD的中点，连接CG并延长，交BA的延长线于点F，连接FD。
(1)、求证：AB=AF；(2)、若AG=AB，∠BCD=120°，判断四边形ACDF的形状，并证明你的结论。22. 为了了解同学们对垃圾分类知识的知晓程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校环保社团的同学们设计了“垃圾分类知识及投放情况"的问卷，并在本校随机抽取了若干名同学进行了问卷测试，根据测试成绩分布情况，他们将全部成绩分成四组，并绘制了不完整的统计表和如图所示的统计图：分组
频数
频率
60≤x<70
a
b
70≤x<80
24
0.4
80≤x<90
18
c
90≤x≤100
12
0.2
请根据上述统计图表，解答下列问题：
(1)、共抽取了多少名学生进行问卷测试；(2)、补全频数分布直方图；(3)、如果测试成绩不低于80分的为“优秀”，请你估计全校2000名学生中“优秀”的学生有多少人。23. 我们把对角线互相垂直的四边形叫做垂美四边形。
(1)、概念理解：如图1，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由；(2)、性质探究：如图2，四边形ABCD的对角线AC、BD交于点O，AC⊥BD，试证明：AB2+CD2=AD2+BC2；(3)、解决问题：如图3，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE。已知AC=4，AB=5，求GE长。