安徽省六安市叶集区2020-2021学年八年级下学期数学期末试卷
试卷更新日期：2021-07-08 类型：期末考试
一、单项选择题(每小题4分，共10小题，满分40分)
-
1. 下列计算正确的是（ ）A、 ＝3 B、 ＝±3 C、 ＝3 D、 ＝±32. 下列方程中，关于x的一元二次方程有（ ）个。
①x2=0②ax2+bx+c=0③ x2-3= x④(x+1)2=x2-9
A、1 B、2 C、3 D、43. 关于一元二次方程x2﹣2x+1﹣a＝0无实根，则a的取值范围是（ ）A、a＜0 B、a＞0 C、a＜ D、a＞4. 如图，数轴上的点A表示的数是-2，点B表示的数是1，CB⊥AB于B，且BC=2，以点A为圆心，AC为半径画弧交数轴于点D，则点D表示的数为（ ）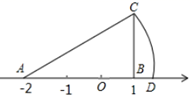
A、 B、 C、 D、25. 如图，在正方形ABCD中，以对角线BD为边作菱形BDFE，连接BF，则∠AFB=（ ）
A、30° B、25° C、22.5° D、不能确定6. 在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，则重叠部分△AFC的面积为（ ）
A、12 B、10 C、8 D、67. 若方程 有增根，则它的增根是（ ）A、0 B、1 C、-1 D、±18. 在某班30位男生跳高成绩绘制的频数直方图中，若各个小矩形的高的比依次是2：3：4：1，则第二个小矩形表示的频数是（ ）A、14 B、12 C、9 D、89. 如图，在边长为4的等边三角形ABC中，点D，E分别是边BC，AC的中点，DF⊥AB于点F，连结EF，则EF的长为（ ）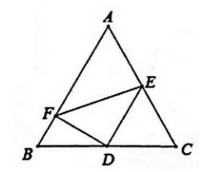
A、 B、2.5 C、 D、310. 在矩形ABCD中，AB=2，AD=3，E是BC边上一点，将△ABE沿AE折叠，使点B落在点B'处，连接CB'，则CB'的最小值是（ ）
A、 -2 B、 +2 C、 -3 D、1二、填空题(每小题5分，共4小题，满分20分)
-
11. 一元二次方程x2=(-4)2的解为 .12. 使式子 成立的x取值范围是13. 若样本x1+1，x2+1，……，xn+1的平均数是10，方差是2，则样本2x1+2，
2x2+2，……，2xn+2的平均数是 ， 方差是。
14. 如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD、CG，有下列结论：①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ABD= AB2 ， 其中正确的结论有 (填序号)。
三、解答题(共90分)
-
15. 计算:16. 解方程： 2x2+3x-1=0 .17. 对干任意实数k，方程(k2+1)x2-2(k+a)2x+k2+4k+b= 0总有一个根1。(1)、求实数a，b；(2)、当k=5时，求方程的另一个根。18. 某商店从厂家以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品的售价为a元，则可卖出(350-10a)件，但物价局限定每件物品加价不能超过进价的20%，商店计划要赚400元，需要卖出多少件商品？每件商品售价多少元？19. 已知元二次方程x2- x+ =0两个根为a，b，求下列各式的值。(1)、(2)、a2+ b+320. 已知关于x的一元二次方程(x-m)2+6x=4m-3有实数根。(1)、求m的取值范围；(2)、设方程的两实根分别为x1与x2 ，
若x1x2-x12-x22=-7，求m的值。
21. 如图，△ABC中，∠ACB=90°，D，E分别是BC，BA的中点，连接DE，F在DE的延长线上，且AF=AE。
(1)、求证：四边形ACEF是平行四边形；(2)、若四边形ACEP是菱形，求∠B的度数。22. 某校开展古诗词诵读大赛活动，现随机抽取部分同学的成绩进行统计，并绘制成如下的两个不完整的统计图，请结合图中提供的信息，解答下列各题：
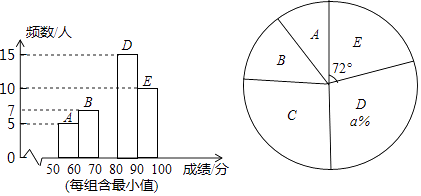(1)、直接写出a的值，a= ， 并把频数分布直方图补充完整 ；(2)、求扇形B的圆心角度数；(3)、如果全校有2000名学生参加这次活动，90分以上(含90分)为优秀，那么估计获得优秀奖的学生有多少人。23. 如图①，已知正方形ABCD的边长为1，点E为边AB上一点，EF⊥EC，且EF=EC，连接AF。
(1)、求证∠EAF的度数：若不变，请求出其值：若改变，请简述理由。
(2)、如图②，连接CF交BD于M，求证：M为CF的中点；(3)、如图②，当点E在正方形ABCD的边AB上运动时，式子AF+2DM的值是否改变？