天津市河西区2020-2021学年七年级下学期数学期末试卷
试卷更新日期：2021-07-08 类型：期末考试
一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，
-
1. 在平面直角坐标系中，点(5，-2)所在的象限为（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列各数中，是不等式x+3>6的解的是（ ）A、4 B、3 C、1 D、-23. 下列调查中，最适合采用全面调查的是（ ）A、了解一批电脑的使用寿命 B、了解某鱼塘中鱼的数量 C、了解电视栏目《朗读者》的收视率 D、了解某校七年一班学生对国家“一带一路"战略的知晓宰4. 估计 的值在（ ）A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间5. 在平面直角坐标系中，把点p(-3，2)向左平移个单位长度，所得到的对应点p'的坐标为（ ）A、(-3，2- ) B、(-3，2+ ) C、(-3- ，2) D、(-3+ ，2)6. 如图所示，三角形ABC中，∠BAC=90°，过点A画AD⊥BC。则下列说法不正确的是（ ）
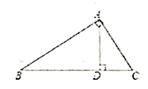A、线段AD是点A与直线BC上各点连接的所有线段中最短的 B、线段AB是点B到直线AD的垂线段 C、点A到直线BC的距离是线段AD的长 D、点C到直线AB的距离是线段AC的长7. 下面是甲、乙两人10次射击成绩(环数)的条形统计图，则下列说法正确的是（ ）
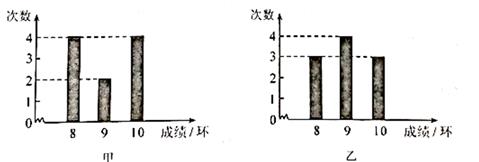A、甲、乙两人的成绩一样稳定 B、乙比甲的成绩稳定 C、甲比乙的成绩稳定 D、无法确定谁的成绩更稳定8. 已知实数a，b，且a>b，则下列结论错误的是（ ）A、a-6>b-6 B、3+a>3+b C、-4a>-4b D、9. 我国古代数学著作《孙子算经》中有“鸡兔同笼"问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？“通过计算鸡和兔的数众分别为（ ）A、23和12 B、12和23 C、24和12 D、12和2410. 如图，在一块长方形草地上原有一条等宽的笔直小路，现在要把这条小路改为同样宽度的等宽弯曲小路，则下列结论正确的有（ ）
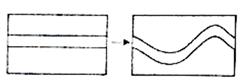A、改造后小路的长度不变 B、改造后小路的长度变小 C、改造后草地部分的面积变小 D、改造后草地部分的面积不变二、填空题：本大题共6小题，每小题3分，共18分，请将答案直接填在题中横线上。
-
11. 若2a+1表示负数，则a需要满足的条件为12. 任意写出一个解为 的二元一次方程组13. 如图，四边形OBCD是正方形，O，D两点的坐标分别是(0，0)，（0，5)，点C在第一象限，则点C的坐标是
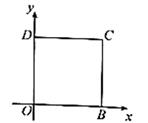14. 某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试。他们的成绩如下表所示：候选人
甲
乙
丙
丁
测试成绩(百分制)
面试
86
92
90
83
笔试
90
83
83
92
如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取
15. 商店为了对某种商品促销，将定价为3元的商品，以下列方式优惠销售：若购买不超过五件，按原价付款；若一次性购买五件以上超过部分打八折，现有39元钱，最多可以购买该商品的件数为16. 我国数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根，华罗庚脱口说出答案39，邻座的乘客忙问计算的奥妙(1)、下面是探究 的过程，请补充完整：①由103=1000，1003=1000000，可以确定 是两位数；
②由59319的个位上的数是9，可以确定 的个位上的数是9：
③如果划去59319后面的三位319得到数59，而33=27，44=64，可以确定 的十位上的数是；由此求得 =39
(2)、已知103823也是一个整数的立方，请你用类似的方法求 =三、解答题：本大题共7小题，共S2分．解答应写出文字说明、演算步骤或证明过程．
-
17. 解方程组 ．18. 解不等式组
请结合题意填空，完成本题的解答。
(Ⅰ)解不等式①，得；
(Ⅱ)解不等式②，得
(Ⅲ)把不等式①和②的解集在数轴上表示出来：
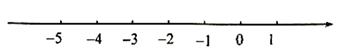
(Ⅳ)原不等式组的解集为
19. 为了推动阳光体育运动的广泛开展，引导学生走向操场、走进大自然、走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：
(1)、本次接受随机抽样调查的学生人数为 ， 图①中m的值为。(2)、求本次调查获取的样本数据的众数和中位数；(3)、根据样本数据，若学校计划购买200双运动鞋，建议购买37号运动鞋多少双？20. 如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA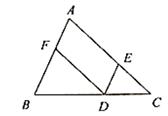
(1)、当∠A=70°时，求∠DEC的度数(2)、求证：∠A=∠EDF21. 某工厂计划招聘A，B两个工种的工人共120人，A，B两个工种的工人月工资分别为3200元和4000元。若该工厂每月支付工人的工资为440000元，那么A，B两个工种的工人各招聘多少人？设招聘A工种的工人x人，招聘B工种的工人y人，
(1)、根据题意填空：根据题意，列方程组得
(2)、完成对本题的解答：22. 在平面直角坐标系xOy中有A，B，C，D四点，其中A(-4，4)，B(4，4)，C(-2，-1)，D(2，-1)。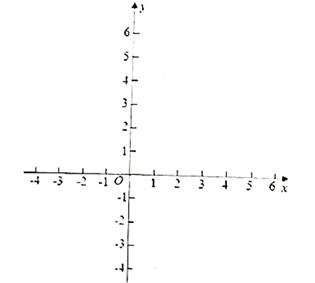
(1)、在下图中描出A，B，C，D四点，再连接AB，CD；(2)、直接写出线段AB与线段CD的位置关系；(3)、若AB与y轴交于点M，CD与y轴交于点N，在线段MN上是否存在一点P，使得三角形ABP与三角形CDP的面积相等．若存在，求点P的坐标；若不存在，请说明理由。23. 如图，在平面直角坐标系中，AB∥CD∥x轴，BC∥DE∥y轴，且AB=CD=4cm，OA=5cm，DE=2cm，动点P从点A出发，以每秒1 cm的速度，沿ABC路线向点C运动；动点2从点o出发，以每秒2cm的速度，沿OED路线向点D运动。若P，Q两点同时出发，其中一点到达终点时，运动停止。
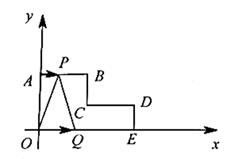(1)、直接写出B，C，D三个点的坐标；(2)、设两点运动的时间为1秒，用含t的式子表示运动过程中三角形OPQ的面积；(3)、当三角形OPQ的面积的范围小于16时，求运动的时间t的范围。