山西省太原市2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-07-08 类型:期末考试
一、选择题(本大题含 10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项符合题目要求,请将其字母标号填入下表相应位置。
-
1. 计算m2·m3的结果,正确的是( )A、m5 B、m6 C、m9 D、5m2. 下列事件中的必然事件是( )A、抛掷一枚图钉,落地后钉尖朝上 B、400人中有2人的生日在同一天 C、车辆随机到达一个路口,遇到绿灯 D、打开电视机,它正播放动画片3. 垃圾分类可提高垃圾的资源价值和经济价值,减少资源消耗,具有社会经济、生态等几方面的效益。《太原市生活垃圾分类管理条例》要求住宅区以及单位应当设置“可回收物、有害垃圾、易腐垃圾、其他垃圾”四类收集容器,并将垃圾分类投放到相应的垃圾收集容器内。下列图形分别是四类垃圾的图标,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算结果正确的是( )A、(a+1)2=a2+1 B、(a+2)(a+3)=a2+6 C、(a+1)(a-1)=a2-1 D、(-a-1)(a+1)=a2-15. 如图,下列条件中能判定直线l1∥l2的是( )
4. 下列计算结果正确的是( )A、(a+1)2=a2+1 B、(a+2)(a+3)=a2+6 C、(a+1)(a-1)=a2-1 D、(-a-1)(a+1)=a2-15. 如图,下列条件中能判定直线l1∥l2的是( )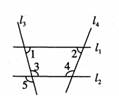 A、∠1=∠2 B、∠1+∠3= 180° C、∠4=∠5 D、∠3=∠56. 2021年2月22日,嫦娥五号带回的部分月壤在人民大会堂首次公开亮相。“月壤”是月球表面的一层细腻沙土,平均粒径约为0.0001米,具有极高的科研价值。数据“0.0001米”用科学记数法表示为( )
A、∠1=∠2 B、∠1+∠3= 180° C、∠4=∠5 D、∠3=∠56. 2021年2月22日,嫦娥五号带回的部分月壤在人民大会堂首次公开亮相。“月壤”是月球表面的一层细腻沙土,平均粒径约为0.0001米,具有极高的科研价值。数据“0.0001米”用科学记数法表示为( ) A、1.0×10-4米 B、1.0×10-6米 C、1.0×10-8米 D、0.1×10-6米7. 已知抛一枚均匀硬币正面朝上的概率为 ,下列说法错误的是( )A、通过抛-枚均匀硬币确定篮球赛中谁先发球是公平的 B、大量重复拋一枚均匀硬币,出现正面朝上的频率稳定 C、连续抛一枚均匀硬币10次可能都是正面朝上 D、连续抛一枚均匀硬币2次必有1次正面朝上8. 如图,已知∠ABC=∠DCB,AC与DB相交于点O。若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( )
A、1.0×10-4米 B、1.0×10-6米 C、1.0×10-8米 D、0.1×10-6米7. 已知抛一枚均匀硬币正面朝上的概率为 ,下列说法错误的是( )A、通过抛-枚均匀硬币确定篮球赛中谁先发球是公平的 B、大量重复拋一枚均匀硬币,出现正面朝上的频率稳定 C、连续抛一枚均匀硬币10次可能都是正面朝上 D、连续抛一枚均匀硬币2次必有1次正面朝上8. 如图,已知∠ABC=∠DCB,AC与DB相交于点O。若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( ) A、∠A=∠D B、AB=CD C、∠ACB=∠DBC D、AC=BD9. 如图,△ABC中,∠BAC=90°,AB=AC=2cm,AO⊥BC于点O。点P是两条直角边上一动点,点P从点B出发,沿BA-AC运动到点C停止。设P点运动的路程为x(cm),△POB的面积为y(cm2),则y随x变化关系的图象为( )
A、∠A=∠D B、AB=CD C、∠ACB=∠DBC D、AC=BD9. 如图,△ABC中,∠BAC=90°,AB=AC=2cm,AO⊥BC于点O。点P是两条直角边上一动点,点P从点B出发,沿BA-AC运动到点C停止。设P点运动的路程为x(cm),△POB的面积为y(cm2),则y随x变化关系的图象为( ) A、
A、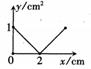 B、
B、 C、
C、 D、
D、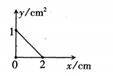 10. 数学课上,同学们用△ABC纸片进行折纸操作,按照下列各图所示的折叠过程和简要的文字说明,折痕AD是△ABC中线的是( )A、沿AD折叠,点C落在BC边上的点E处
10. 数学课上,同学们用△ABC纸片进行折纸操作,按照下列各图所示的折叠过程和简要的文字说明,折痕AD是△ABC中线的是( )A、沿AD折叠,点C落在BC边上的点E处 B、沿AD折叠,点C落在AB边上的点E处
B、沿AD折叠,点C落在AB边上的点E处  C、先沿DE折叠使点C与B重合,再沿AD折叠得到折痕AD
C、先沿DE折叠使点C与B重合,再沿AD折叠得到折痕AD  D、沿AD折叠,点C落在三角形外的点E处
D、沿AD折叠,点C落在三角形外的点E处 
二、填空题(本大题含5个小题,每小题2分,共10分)将答案直接写在题中横线上。
-
11. 计算3-2的结果为12. 如图1,小明用尺规作出∠AOB的角平分线OC。为探索作图的道理,在图1中连接CE,CD得到图2,根据作法可得△COE≌△COD.他判定两个三角形全等的依据是
 13. 如图是一个数值转换机,将自变量x值输入,输出的是因变量y的值。其中y与x的部分对应值如右表所示,根据表中数据,该数值转换机确定的y与x的关系式为
13. 如图是一个数值转换机,将自变量x值输入,输出的是因变量y的值。其中y与x的部分对应值如右表所示,根据表中数据,该数值转换机确定的y与x的关系式为
x
……
-1
0
1
2
3
4
……
y
……
-2
0
2
4
6
8
……
14. 如图,是一个面积为4cm2正方形微信二维码。小明利用所学概率知识估算二维码中黑色部分的面积,在正方形区域内随机掷点,经过大量重复试验,发现点落人黑色部分的频率稳定在0.7左右,据此可估计黑色部分的面积约为 15. 如图,在△ABC中,AB=AC,∠BAC=a,AD是BC边上的中线,以D为圆心,DC的长为半径的半圆交AD于点E,交AC于点F,连接EF,DF。请从下面A,B两题中任选一题作答。我选择( )题:
15. 如图,在△ABC中,AB=AC,∠BAC=a,AD是BC边上的中线,以D为圆心,DC的长为半径的半圆交AD于点E,交AC于点F,连接EF,DF。请从下面A,B两题中任选一题作答。我选择( )题: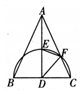
A.∠AFD=°(用含α的式子表示)
B.∠AFE=°
三、解答题(本大题含8个小题,共60分)解答应写出必要的文字说明、推理过程或演算步骤。
-
16.(1)、计算:(-2x)3·(x2y)2;(2)、计算:(x+2y)(2x-3y);(3)、先化简,再求值:[(a-2)2+(a+2)(a-2)]+(2a),其中a=8。17. 如图,已知∠α,∠β和线段c。求作:△ABC,使∠A=∠α,∠B=∠β,AB=c。(要求:在指定的作图区域内用尺规作图,保留作图痕迹,不写画法)
 18. 小明和小亮在学习概率后设计了一个游戏:任意掷一枚质地均匀的骰子,掷出的点数大于4,小明获胜;掷出的点数小于4,小亮获胜。请通过计算说明这个游戏是否公平;若不公平,请你修改游戏规则,使其公平.19. 如图,已知点E,F在线段BD上,AD∥BC,BF=DE,∠A=∠C。试判断线段AF与CE的数量关系和位置关系,并说明理由。
18. 小明和小亮在学习概率后设计了一个游戏:任意掷一枚质地均匀的骰子,掷出的点数大于4,小明获胜;掷出的点数小于4,小亮获胜。请通过计算说明这个游戏是否公平;若不公平,请你修改游戏规则,使其公平.19. 如图,已知点E,F在线段BD上,AD∥BC,BF=DE,∠A=∠C。试判断线段AF与CE的数量关系和位置关系,并说明理由。 20. 一直以来,人们力图探寻地球内部的奥秘,科学家做了大量的模拟试验后发现:地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可近似地表示为y=35x+20
20. 一直以来,人们力图探寻地球内部的奥秘,科学家做了大量的模拟试验后发现:地表以下岩层的温度y(℃)随着所处深度x(km)的变化而变化,在某个地点y与x之间的关系可近似地表示为y=35x+20 (1)、根据关系式,下表列出部分因变量y与自变量x的对应值,请补充表中所缺的数据;
(1)、根据关系式,下表列出部分因变量y与自变量x的对应值,请补充表中所缺的数据;所处深度x( km)
2
3
4
5
6
7
……
岩层的温度y(℃)
90
125
195
265
……
(2)、当所处深度x( km)每增加1km,岩层的温度y(℃)是怎样变化的?(3)、当岩层的温度y(℃)达到1000℃时,根据上述关系式,求所处的深度。21. 如图,已知直线EF∥MN,△ABC的顶点B,C分别在直线MN和EF上,AB与EF交于点D。若△ABC中,∠ACB=90°,∠A=30°,EF恰好平分∠ACB,求∠ABM的度数。 22. 阅读下列材料,解决相应问题:
22. 阅读下列材料,解决相应问题:“友好数对”
已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原两个两位数均不同的新数,若这两个两位数的乘积与交换位置后两个新两位数的乘积相等,则称这样的两个两位数为“友好数对”。例如:43×68=34×86=2924,所以43和68与34和86都是“友好数对”。
(1)、为探究“友好数对”的本质,可设“友好数对”中一个数的十位数字为a,个位数字为b,且a≠b;另一个数的十位数字为c,个位数字为d,且c≠d,则a,b,c,d之间存在一个等量关系,其探究和说理过程如下,请你将其补充完整。解:根据题意,“好友数对”中的两个数分别表示为10a+b和10c+d ,将它们各自的十位数字和个位数字交换位置后两个数依次表示为和
因为它们是友好数对,
所以(10a+b)(10c+d)=
即a,b,c,d的等量关系为:
(2)、请从下面A,B两题中任选一题作答,我选择 题。A.请再写出一对“友好数对”,与本题已给的“友好数对”不同。
B.若有一个两位数,十位数字为x+2,个位数字为x,另一个两位数,十位数字为x+2,个位数字为x+8。且这两个数为“友好数对”,直接写出这两个两位数。
(3)、36和84“友好数对”. (填“是”或“不是”)23. 综合与实践:问题情境:如图1,在△ABC中,AB=AC,∠BAC为钝角,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F。试判断线段DE与DF的数量关系,并说明理由。
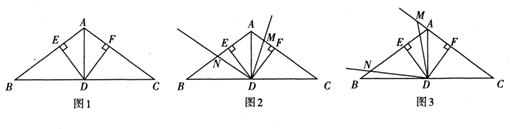
探究展示:小宇同学展示出如下正确的解法:
解:DE=DF,理由如下:
∵点D是BC的中点,∴AD是BC边上中线,
∵AB=AC,∴AD是∠BAC的角平分线(依据1)
∵DF⊥AC,DE⊥AB,∴DE=DF。(依据2)
(1)、请探究线段AE与AF的数量关系,并说明理由。(2)、拓展延伸:
请从下面A,B两题中任选一题作答。我选择题。A.在图1的条件下,点M是线段AF上一点,作∠MDN=∠EDF,射线DN交AB于点N,试判断AM+EN=AE是否成立,并说明理由。
B.在图1的条件下,点M是线段FA延长上一点,作∠MDN=∠EDF,射线DN交线段BE于点N,试写出AM,EN与AE的等量关系并说明理由。
(3)、反思交流:
写出上述过程中的“依据1”和“依据2”:依据1:;
依据2:。