2021年高考数学真题试卷(天津卷)
试卷更新日期:2021-07-08 类型:高考真卷
一、选择题,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 ,则 ( )A、 B、 C、 D、2. 已知 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不允分也不必要条件3. 函数 的图像大致为( )A、
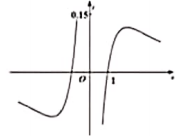 B、
B、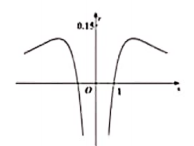 C、
C、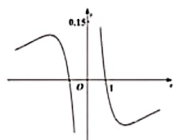 D、
D、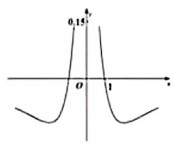 4. 从某网格平台推荐的影视作品中抽取400部,统计其评分分数据,将所得400个评分数据分为8组: ,并整理得到如下的费率分布直方图,则评分在区间 内的影视作品数量是( )
4. 从某网格平台推荐的影视作品中抽取400部,统计其评分分数据,将所得400个评分数据分为8组: ,并整理得到如下的费率分布直方图,则评分在区间 内的影视作品数量是( ) A、20 B、40 C、64 D、805. 设 ,则a , b , c的大小关系为( )A、 B、 C、 D、6. 两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为 ,两个圆锥的高之比为 ,则这两个圆锥的体积之和为( )A、 B、 C、 D、7. 若 ,则 ( )A、-1 B、 C、1 D、8. 已知双曲线 的右焦点与抛物线 的焦点重合,抛物线的准线交双曲线于A , B两点,交双曲钱的渐近线于C、D两点,若 .则双曲线的离心率为( )A、 B、 C、2 D、39. 设 ,函数 ,若 在区间 内恰有6个零点,则a的取值范围是( )A、 B、 C、 D、 .
A、20 B、40 C、64 D、805. 设 ,则a , b , c的大小关系为( )A、 B、 C、 D、6. 两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为 ,两个圆锥的高之比为 ,则这两个圆锥的体积之和为( )A、 B、 C、 D、7. 若 ,则 ( )A、-1 B、 C、1 D、8. 已知双曲线 的右焦点与抛物线 的焦点重合,抛物线的准线交双曲线于A , B两点,交双曲钱的渐近线于C、D两点,若 .则双曲线的离心率为( )A、 B、 C、2 D、39. 设 ,函数 ,若 在区间 内恰有6个零点,则a的取值范围是( )A、 B、 C、 D、 .二、填空题,本大题共6小题,每小题5分,共30分,试题中包含两个空的,答对1个的给3分,全部答对的给5分.
-
10. i是虚数单位,复数 .11. 在 的展开式中, 的系数是 .12. 若斜率为 的直线与y轴交于点A , 与圆 相切于点B , 则 .13. 若 ,则 的最小值为 .14. 甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局,已知每次活动中,甲、乙猜对的概率分别为 和 ,且每次活动中甲、乙猜对与否互不影响,各次活动也互不影响,则一次活动中,甲获胜的概率为 , 3次活动中,甲至少获胜2次的概率为 .15. 在边长为1的等边三角形ABC中,D为线段BC上的动点, 且交AB于点E . 且交AC于点F , 则 的值为; 的最小值为 .
三、解答题,本大题共5小题,共75分,解答应写出文字说明,证明过程成演算步骤.
-
16. 在 ,角 所对的边分别为 ,已知 , .(1)、求a的值;(2)、求 的值;(3)、求 的值.17. 如图,在棱长为2的正方体 中,E为棱BC的中点,F为棱CD的中点.
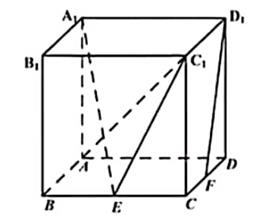 (1)、求证: 平面 ;(2)、求直线 与平面 所成角的正正弦值.(3)、求二面角 的正弦值.18. 已知椭圆 的右焦点为F , 上顶点为B , 离心率为 ,且 .(1)、求椭圆的方程;(2)、直线l与椭圆有唯一的公共点M , 与y轴的正半轴交于点N , 过N与BF垂直的直线交x轴于点P . 若 ,求直线l的方程.
(1)、求证: 平面 ;(2)、求直线 与平面 所成角的正正弦值.(3)、求二面角 的正弦值.18. 已知椭圆 的右焦点为F , 上顶点为B , 离心率为 ,且 .(1)、求椭圆的方程;(2)、直线l与椭圆有唯一的公共点M , 与y轴的正半轴交于点N , 过N与BF垂直的直线交x轴于点P . 若 ,求直线l的方程.