全国历年中考数学真题精选汇编:二次函数2
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 已知抛物线 ( 是常数, )经过点 ,其对称轴是直线 .有下列结论:
① ;②关于x的方程 有两个不等的实数根;③ .其中,正确结论的个数是( )
A、0 B、1 C、2 D、32. 已知抛物线y=x2﹣4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为( )A、y=x2+2x+1 B、y=x2+2x﹣1 C、y=x2﹣2x+1 D、y=x2﹣2x﹣13. 如图,在四边形 中, , , , , .动点M,N同时从点A出发,点M以 的速度沿 向终点B运动,点N以 的速度沿折线 向终点C运动.设点N的运动时间为 , 的面积为 ,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、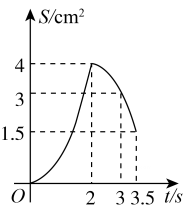 C、
C、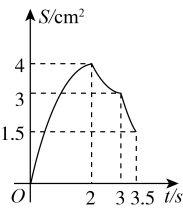 D、
D、 4. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:
4. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象给出下列结论:①ac<0;
②4a﹣2b+c>0;
③当x>2时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的结论有( )
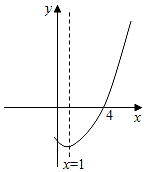 A、1个 B、2个 C、3个 D、4个5. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为 ,且经过点(2,0). 下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若 , 是抛物线上的两点,则y1<y2;⑤ b>m(am+b) (其中m≠ ).其中说法正确的是( )
A、1个 B、2个 C、3个 D、4个5. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为 ,且经过点(2,0). 下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若 , 是抛物线上的两点,则y1<y2;⑤ b>m(am+b) (其中m≠ ).其中说法正确的是( )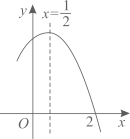 A、①②④⑤ B、①②④ C、①④⑤ D、③④⑤6. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )
A、①②④⑤ B、①②④ C、①④⑤ D、③④⑤6. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )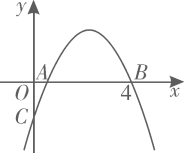 A、5 B、4 C、3 D、27. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )
A、5 B、4 C、3 D、27. 如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2 , y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1 , 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和 其中正确结论的个数是( )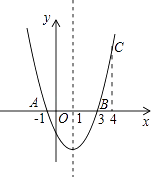 A、1 B、2 C、3 D、48. 已知抛物线 与 轴的交点为A(1,0)和B(3,0),点P1( , ),P2( , )是抛物线上不同于A,B的两个点,记△P1AB的面积为S1 , △P2AB的面积为S2。有下列结论:①当 时,S1>S2;②当 时,S1<S2;③当 时,S1>S2;④当 时,S1<S2。其中正确结论的个数是A、1 B、2 C、3 D、49. 如图,二次函数 (a>0)的图象与x轴交于A,B两点,与y轴正半轴交于点C,它的对称轴为直线x=-1.则下列选项中正确的是( )
A、1 B、2 C、3 D、48. 已知抛物线 与 轴的交点为A(1,0)和B(3,0),点P1( , ),P2( , )是抛物线上不同于A,B的两个点,记△P1AB的面积为S1 , △P2AB的面积为S2。有下列结论:①当 时,S1>S2;②当 时,S1<S2;③当 时,S1>S2;④当 时,S1<S2。其中正确结论的个数是A、1 B、2 C、3 D、49. 如图,二次函数 (a>0)的图象与x轴交于A,B两点,与y轴正半轴交于点C,它的对称轴为直线x=-1.则下列选项中正确的是( ) A、 B、 C、 D、当 (n为实数)时,
A、 B、 C、 D、当 (n为实数)时,二、填空题
-
10. 对任意实数 ,若多项式 的值总大于 ,则实数 的取值范围是 .
三、解答题
-
11. 已知抛物线y=x2﹣bx+c(b , c为常数,b>0)经过点A(﹣1,0),点M(m , 0)是x轴正半轴上的动点.
(Ⅰ)当b=2时,求抛物线的顶点坐标;
(Ⅱ)点D(b , yD)在抛物线上,当AM=AD , m=5时,求b的值;
(Ⅲ)点Q(b+ ,yQ)在抛物线上,当 AM+2QM的最小值为 时,求b的值.
四、综合题
-
12. 在平面直角坐标系 中, 为抛物线 上任意两点,其中 .(1)、若抛物线的对称轴为 ,当 为何值时,(2)、设抛物线的对称轴为 .若对于 ,都有 ,求t的取值范围.13. 如图, 是 与弦 所围成的图形的内部的一定点, 是弦 上一动点,连接 并延长交 于点 ,连接 .已知 ,设 , 两点间的距离为 , , 两点间的距离为 , , 两点间的距离为 .

小腾根据学习函数的经验,分别对函数 , 随自变量 的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)、按照下表中自变量 的值进行取点、画图、测量,分别得到了 , 与 的几组对应值;0
1
2
3
4
5
6
(2)、在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点( , ),( , ),并画出函数 , 的图象; (3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .14. 综合与探究
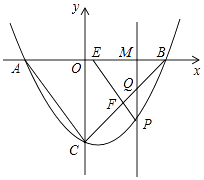
(3)、结合函数图象,解决问题:当 为等腰三角形时, 的长度约为 .14. 综合与探究如图,抛物线y= 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.
 (1)、求A,B,C三点的坐标
(1)、求A,B,C三点的坐标
(2)、试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)、请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.15. 如图所示,抛物线y=ax2﹣ x+c经过原点O与点A(6,0)两点,过点A作AC⊥x轴,交直线y=2x﹣2于点C,且直线y=2x﹣2与x轴交于点D.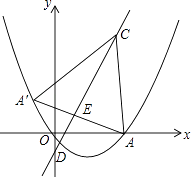 (1)、求抛物线的解析式,并求出点C和点D的坐标;(2)、求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;(3)、点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.16. 已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ,﹣ ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.(1)、求该二次函数的解析式,及顶点D的坐标;(2)、求|PC﹣PD|的最大值及对应的点P的坐标;(3)、设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.17. 如图,抛物线 与 轴相交于点 和点 ,与 轴相交于点 ,作直线 .
(1)、求抛物线的解析式,并求出点C和点D的坐标;(2)、求点A关于直线y=2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由;(3)、点P(x,y)是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值.16. 已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ,﹣ ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.(1)、求该二次函数的解析式,及顶点D的坐标;(2)、求|PC﹣PD|的最大值及对应的点P的坐标;(3)、设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.17. 如图,抛物线 与 轴相交于点 和点 ,与 轴相交于点 ,作直线 .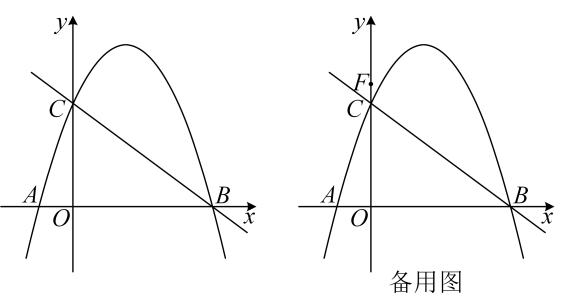 (1)、求抛物线的解析式;(2)、在直线 上方的抛物线上存在点 ,使 ,求点 的坐标;(3)、在(2)的条件下,点 的坐标为 ,点 在抛物线上,点 在直线 上,当以 为顶点的四边形是平行四边形时,请直接写出点 的坐标.18. 在平面直角坐标系中,抛物线 交x轴于 两点,交y轴于点C.
(1)、求抛物线的解析式;(2)、在直线 上方的抛物线上存在点 ,使 ,求点 的坐标;(3)、在(2)的条件下,点 的坐标为 ,点 在抛物线上,点 在直线 上,当以 为顶点的四边形是平行四边形时,请直接写出点 的坐标.18. 在平面直角坐标系中,抛物线 交x轴于 两点,交y轴于点C.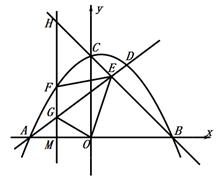
 (1)、求抛物线的表达式;(2)、如图,直线 与抛物线交于A,D两点,与直线 于点E.若 是线段 上的动点,过点M作x轴的垂线,交抛物线于点F,交直线 于点G,交直线 于点H.
(1)、求抛物线的表达式;(2)、如图,直线 与抛物线交于A,D两点,与直线 于点E.若 是线段 上的动点,过点M作x轴的垂线,交抛物线于点F,交直线 于点G,交直线 于点H.①当点F在直线 上方的抛物线上,且 时,求m的值;
②在平面内是否在点P,使四边形 为正方形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
19. 如图,二次函数 的图象交x轴于点 , ,交y轴于点C.点 是x轴上的一动点, 轴,交直线 于点M,交抛物线于点N. (1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;
(1)、求这个二次函数的表达式;(2)、①若点P仅在线段 上运动,如图1.求线段 的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
20. 如图1,在平面直角坐标系中,抛物线 与 轴交于 , 两点, 点坐标为 ,与 轴交于点 ,直线 与抛物线交于 , 两点.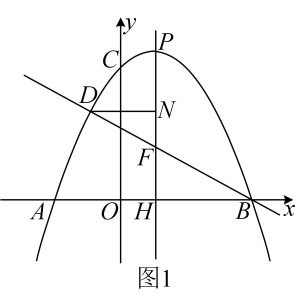 (1)、求抛物线的函数表达式;(2)、求 的值和 点坐标;(3)、点 是直线 上方抛物线上的动点,过点 作 轴的垂线,垂足为 ,交直线 于点 ,过点 作 轴的平行线,交 于点 ,当 是线段 的三等分点时,求 点坐标;(4)、如图2, 是 轴上一点,其坐标为 ,动点 从 出发,沿 轴正方向以每秒5个单位的速度运动,设 的运动时间为 ( ),连接 ,过 作 于点 ,以 所在直线为对称轴,线段 经轴对称变换后的图形为 ,点 在运动过程中,线段 的位置也随之变化,请直接写出运动过程中线段 与抛物线有公共点时 的取值范围.
(1)、求抛物线的函数表达式;(2)、求 的值和 点坐标;(3)、点 是直线 上方抛物线上的动点,过点 作 轴的垂线,垂足为 ,交直线 于点 ,过点 作 轴的平行线,交 于点 ,当 是线段 的三等分点时,求 点坐标;(4)、如图2, 是 轴上一点,其坐标为 ,动点 从 出发,沿 轴正方向以每秒5个单位的速度运动,设 的运动时间为 ( ),连接 ,过 作 于点 ,以 所在直线为对称轴,线段 经轴对称变换后的图形为 ,点 在运动过程中,线段 的位置也随之变化,请直接写出运动过程中线段 与抛物线有公共点时 的取值范围.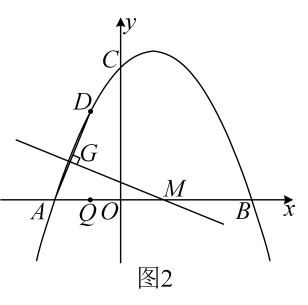 21. 如图,抛物线 与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线 ,点C坐标为 .
21. 如图,抛物线 与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线 ,点C坐标为 . (1)、求抛物线表达式;(2)、在抛物线上是否存在点P,使 ,如果存在,求出点P坐标;如果不存在,请说明理由;(3)、在(2)的条件下,若点P在x轴上方,点M是直线BP上方抛物线上的一个动点,求点M到直线BP的最大距离;(4)、点G是线段AC上的动点,点H是线段BC上的动点,点Q是线段AB上的动点,三个动点都不与点 重合,连接 ,得到 ,直接写出 周长的最小值.22. 在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)、求抛物线表达式;(2)、在抛物线上是否存在点P,使 ,如果存在,求出点P坐标;如果不存在,请说明理由;(3)、在(2)的条件下,若点P在x轴上方,点M是直线BP上方抛物线上的一个动点,求点M到直线BP的最大距离;(4)、点G是线段AC上的动点,点H是线段BC上的动点,点Q是线段AB上的动点,三个动点都不与点 重合,连接 ,得到 ,直接写出 周长的最小值.22. 在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D. (1)、求抛物线的解析式;(2)、点P为直线CD上的一个动点,连接BC;
(1)、求抛物线的解析式;(2)、点P为直线CD上的一个动点,连接BC;①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
23. 如图,在平面直角坐标系中,O是坐标原点,抛物线 经过点 和点 ,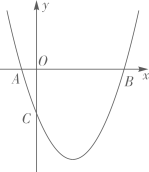 (1)、求抛物线的表达式;(2)、如图,线段 绕原点O逆时针旋转30°得到线段 .过点 作射线 ,点M是射线 上一点(不与点B重合),点M关于x轴的对称点为点N,连接
(1)、求抛物线的表达式;(2)、如图,线段 绕原点O逆时针旋转30°得到线段 .过点 作射线 ,点M是射线 上一点(不与点B重合),点M关于x轴的对称点为点N,连接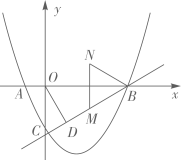
①请直接写出 的形状为_▲_.
②设 的面积为 的面积为是 ,当 时,求点M的坐标;
(3)、如图,在(2)的结论下,过点B作 ,交 的延长线于点E,线段 绕点B逆时针旋转,旋转角为 得到线段 ,过点F作 轴,交射线 于点K, 的角平分线和 的角平分线相交于点G,当 时,请直接写出点G的坐标为. 24. 在平面直角坐标系中,抛物线 经过点 和点 ,与y轴交于点D,与x轴的另一交点为点B.
24. 在平面直角坐标系中,抛物线 经过点 和点 ,与y轴交于点D,与x轴的另一交点为点B.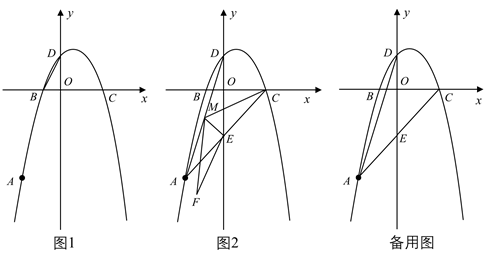 (1)、求抛物线的解析式;(2)、如图1,连接 ,在抛物线上是否存在点P,使得 ?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、如图2,连接 ,交y轴于点E,点M是线段 上的动点(不与点A,点D重合),将 沿 所在直线翻折,得到 ,当 与 重叠部分的面积是 面积的 时,请直接写出线段 的长.25. 如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.
(1)、求抛物线的解析式;(2)、如图1,连接 ,在抛物线上是否存在点P,使得 ?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、如图2,连接 ,交y轴于点E,点M是线段 上的动点(不与点A,点D重合),将 沿 所在直线翻折,得到 ,当 与 重叠部分的面积是 面积的 时,请直接写出线段 的长.25. 如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.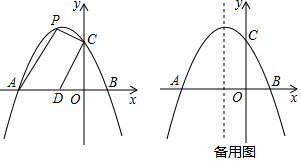 (1)、求这个抛物线的函数表达式.(2)、点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.(3)、点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.26. 在平面直角坐标系中,函数 ( 为常数)的图象与y轴交于点A.
(1)、求这个抛物线的函数表达式.(2)、点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.(3)、点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.26. 在平面直角坐标系中,函数 ( 为常数)的图象与y轴交于点A.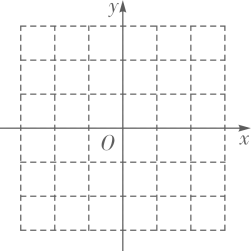 (1)、求点A的坐标.(2)、当此函数图象经过点 时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当 时,若函数 (a为常数)的图象的最低点到直线 的距离为2,求a的值.(4)、设 , 三个顶点的坐标分别为 、 、 .当函数 ( 为常数)的图象与 的直角边有交点时,交点记为点P.过点P作y轴的垂线,与此函数图象的另一个交点为 ( 与P不重合),过点A作y轴的垂线,与此函数图象的另一个交点为 .若 ,直接写出a的值.27. 已知函数y= (n为常数)(1)、当n=5,
(1)、求点A的坐标.(2)、当此函数图象经过点 时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当 时,若函数 (a为常数)的图象的最低点到直线 的距离为2,求a的值.(4)、设 , 三个顶点的坐标分别为 、 、 .当函数 ( 为常数)的图象与 的直角边有交点时,交点记为点P.过点P作y轴的垂线,与此函数图象的另一个交点为 ( 与P不重合),过点A作y轴的垂线,与此函数图象的另一个交点为 .若 ,直接写出a的值.27. 已知函数y= (n为常数)(1)、当n=5,①点P(4,b)在此函数图象上,求b的值
②求此函数的最大值
(2)、已知线段AB的两个端点坐标分别为4(2,2)、B(4,2),当此函数的图象与线段AB只有一个交点时,直接写出n的取值范围.(3)、当此函数图象上有4个点到x轴的距离等于4时,求n的取值范围.28. 《函数的图象与性质》拓展学习片段展示: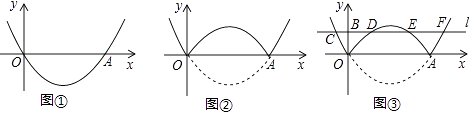 (1)、【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ 经过原点O,与x轴的另一个交点为A,则a= .
(1)、【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ 经过原点O,与x轴的另一个交点为A,则a= .
(2)、【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.(3)、【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.(4)、【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.29. 已知抛物线y=ax2+bx+3的对称轴为直线x= ,交x轴于点A、B,交y轴于点C,且点A坐标为A(-2,0),直线y=-mx-n(m>0)与抛物线交于点P、Q(点P在点Q的右边),交y轴于点H (1)、求该抛物线的解析式(2)、若n=5,且△CPQ的面积为3,求m的值(3)、当m≠1时,若n=-3m,直线AQ交y轴于点K.设△PQK的面积为S,求S与m之间的函数解析式。30. 如图,二次函数 ( 是实数,且 )的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 ,已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, .连接 并延长交 轴于点 ,连接 .
(1)、求该抛物线的解析式(2)、若n=5,且△CPQ的面积为3,求m的值(3)、当m≠1时,若n=-3m,直线AQ交y轴于点K.设△PQK的面积为S,求S与m之间的函数解析式。30. 如图,二次函数 ( 是实数,且 )的图象与 轴交于 、 两点(点 在点 的左侧),其对称轴与 轴交于点 ,已知点 位于第一象限,且在对称轴上, ,点 在 轴的正半轴上, .连接 并延长交 轴于点 ,连接 . (1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.31. 甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:
(1)、求 、 、 三点的坐标(用数字或含 的式子表示);(2)、已知点 在抛物线的对称轴上,当 的周长的最小值等于 ,求 的值.31. 甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.
乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;
②月利润=月租车费-月维护费;
③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)、当每个公司租出的汽车为10辆时,甲公司的月利润是元;当每个公司租出的汽车为辆时,两公司的月利润相等;(2)、求两公司月利润差的最大值;(3)、甲公司热心公益事业,每租出1辆汽车捐出a元 给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求a的取值范围.32. 如图,在平面直角坐标系中,函数 的图像交 轴于点 、 ,交 轴于点 ,它的对称轴交 轴于点 .过点 作 轴交抛物线于点 ,连接 并延长交 轴于点 ,交抛物线于点 .直线 交 于点 ,交抛物线于点 ,连接 、 .

备用图
(1)、点 的坐标为:;(2)、当 是直角三角形时,求 的值;(3)、 与 有怎样的位置关系?请说明理由.33. 如图,二次函数 、 的图像分别为 、 , 交 轴于点 ,点 在 上,且位于 轴右侧,直线 与 在 轴左侧的交点为 . (1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .
(1)、若 点的坐标为 , 的顶点坐标为 ,求 的值;(2)、设直线 与 轴所夹的角为 .①当 ,且 为 的顶点时,求 的值;
②若 ,试说明:当 、 、 各自取不同的值时, 的值不变;
(3)、若 ,试判断点 是否为 的顶点?请说明理由.34. 二次函数 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.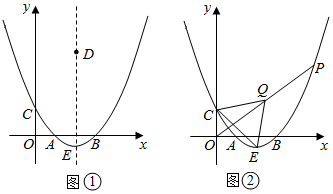 (1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.35. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.36. 有一块矩形地块 , 米, 米,为美观,拟种植不同的花卉,如图所示,将矩形 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形 和 中种植甲种花卉;在等腰梯形 和 中种植乙种花卉;在矩形 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 、60 元/米 、40元/米 ,设三种花卉的种植总成本为y元.
(1)、求这个二次函数的表达式,并写出点E的坐标;(2)、如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;(3)、如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.35. 已知抛物线y=ax2+bx+c经过A(2,0),B(3n﹣4,y1),C(5n+6,y2)三点,对称轴是直线x=1.关于x的方程ax2+bx+c=x有两个相等的实数根.(1)、求抛物线的解析式;(2)、若n<﹣5,试比较y1与y2的大小;(3)、若B,C两点在直线x=1的两侧,且y1>y2 , 求n的取值范围.36. 有一块矩形地块 , 米, 米,为美观,拟种植不同的花卉,如图所示,将矩形 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为x米.现决定在等腰梯形 和 中种植甲种花卉;在等腰梯形 和 中种植乙种花卉;在矩形 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米 、60 元/米 、40元/米 ,设三种花卉的种植总成本为y元.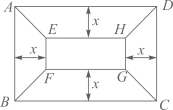 (1)、当 时,求种植总成本y;(2)、求种植总成本y与x的函数表达式,并写出自变量x的取值范围;(3)、若甲、乙两种花卉的种植面积之差不超过120米 ,求三种花卉的最低种植总成本.37. 如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为 ,点D的坐标为 .
(1)、当 时,求种植总成本y;(2)、求种植总成本y与x的函数表达式,并写出自变量x的取值范围;(3)、若甲、乙两种花卉的种植面积之差不超过120米 ,求三种花卉的最低种植总成本.37. 如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为 ,点D的坐标为 . (1)、求该二次函数的表达式;(2)、点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且 ,求点E的坐标.(3)、试问在该二次函数图象上是否存在点G,使得 的面积是 的面积的 ?若存在,求出点G的坐标;若不存在,请说明理由.38. 已知:二次函数 (a为常数).(1)、请写出该二次函数图象的三条性质;(2)、在同一直角坐标系中,若该二次函数的图象在 的部分与一次函数 的图象有两个交点,求 的取值范围.39. 如图,在平面直角坐标系xOy中,抛物线L1: 过点C(0,﹣3),与抛物线L2: 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)、求该二次函数的表达式;(2)、点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且 ,求点E的坐标.(3)、试问在该二次函数图象上是否存在点G,使得 的面积是 的面积的 ?若存在,求出点G的坐标;若不存在,请说明理由.38. 已知:二次函数 (a为常数).(1)、请写出该二次函数图象的三条性质;(2)、在同一直角坐标系中,若该二次函数的图象在 的部分与一次函数 的图象有两个交点,求 的取值范围.39. 如图,在平面直角坐标系xOy中,抛物线L1: 过点C(0,﹣3),与抛物线L2: 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.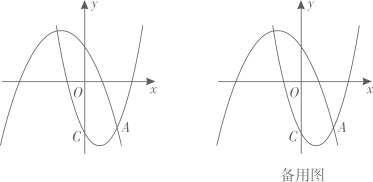 (1)、求抛物线L1对应的函数表达式;(2)、若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;(3)、设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.40. 已知二次函数y=﹣x2+6x﹣5.(1)、求二次函数图象的顶点坐标;(2)、当1≤x≤4时,函数的最大值和最小值分别为多少?(3)、当t≤x≤t+3时,函数的最大值为m , 最小值为n , 若m﹣n=3,求t的值.
(1)、求抛物线L1对应的函数表达式;(2)、若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;(3)、设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.40. 已知二次函数y=﹣x2+6x﹣5.(1)、求二次函数图象的顶点坐标;(2)、当1≤x≤4时,函数的最大值和最小值分别为多少?(3)、当t≤x≤t+3时,函数的最大值为m , 最小值为n , 若m﹣n=3,求t的值.
-
-