全国历年中考数学真题精选汇编:反比例函数2
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 已知A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是反比例函数y= 上的三点,若x1<x2<x3 , y2<y1<y3 , 则下列关系式不正确的是( )A、x1•x2<0 B、x1•x3<0 C、x2•x3<0 D、x1+x2<02. 已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④3. 如图,平行于x轴的直线与函数 (k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为( )
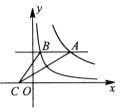 A、8 B、-8 C、4 D、-44. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y= (x<0)图象上一点,AO的延长线交函数y= (x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( )
A、8 B、-8 C、4 D、-44. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y= (x<0)图象上一点,AO的延长线交函数y= (x>0,k是不等于0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,交于x轴于点B,连结AB,AA′,A′C′.若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于( ) A、8 B、10 C、3 D、45. 在平面直角坐标系中,分别过点A(m,0),B(m+2,0)作x轴的垂线l1和l2 , 探究直线l1 , 直线l2与双曲线y= 的关系,下列结论错误的是( )A、两直线中总有一条与双曲线相交 B、当m=1时,两直线与双曲线的交点到原点的距离相等 C、当﹣2<m<0时,两直线与双曲线的交点在y轴两侧 D、当两直线与双曲线都有交点时,这两交点的最短距离是26. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
A、8 B、10 C、3 D、45. 在平面直角坐标系中,分别过点A(m,0),B(m+2,0)作x轴的垂线l1和l2 , 探究直线l1 , 直线l2与双曲线y= 的关系,下列结论错误的是( )A、两直线中总有一条与双曲线相交 B、当m=1时,两直线与双曲线的交点到原点的距离相等 C、当﹣2<m<0时,两直线与双曲线的交点在y轴两侧 D、当两直线与双曲线都有交点时,这两交点的最短距离是26. 如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )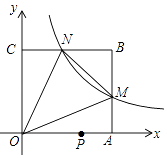 A、6 B、10 C、2 D、27. 在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y= 相交于点A、B,且AC+BC=4,则△OAB的面积为( )
A、6 B、10 C、2 D、27. 在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y= 相交于点A、B,且AC+BC=4,则△OAB的面积为( )
A、2 +3或2 ﹣3 B、 +1或 ﹣1 C、2 ﹣3 D、 ﹣18. 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ,反比例函数y= 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )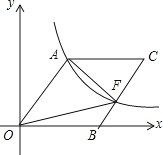 A、60 B、80 C、30 D、409. 如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
A、60 B、80 C、30 D、409. 如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) A、3 B、4 C、6 D、810. 如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
A、3 B、4 C、6 D、810. 如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 (m为1~8的整数).函数 ( )的图象为曲线L.
 (1)、若L过点 ,则k=;(2)、若L过点 ,则它必定还过另一点 ,则m=;(3)、若曲线L使得 这些点分布在它的两侧,每侧各4个点,则k的整数值有个.12. 如图,等腰 的两个顶点 、 在反比例函数 ( )的图象上, .过点C作边 的垂线交反比例函数 ( )的图象于点D,动点P从点D出发,沿射线 方向运动 个单位长度,到达反比例函数 ( )图象上一点,则 .
(1)、若L过点 ,则k=;(2)、若L过点 ,则它必定还过另一点 ,则m=;(3)、若曲线L使得 这些点分布在它的两侧,每侧各4个点,则k的整数值有个.12. 如图,等腰 的两个顶点 、 在反比例函数 ( )的图象上, .过点C作边 的垂线交反比例函数 ( )的图象于点D,动点P从点D出发,沿射线 方向运动 个单位长度,到达反比例函数 ( )图象上一点,则 .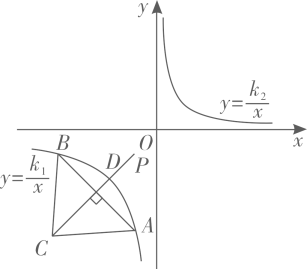 13. 如图,已知在平面直角坐标系xOy中,直线 分别交x轴,y轴于点A和点B,分别交反比例函数 , 的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD. 若△COE的面积与△DOB的面积相等,则k的值是.
13. 如图,已知在平面直角坐标系xOy中,直线 分别交x轴,y轴于点A和点B,分别交反比例函数 , 的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD. 若△COE的面积与△DOB的面积相等,则k的值是.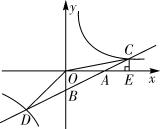 14. 已知△ABC的三个顶点为A ,B ,C ,将△ABC向右平移m( )个单位后,△ABC某一边的中点恰好落在反比例函数 的图象上,则m的值为.15. 如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
14. 已知△ABC的三个顶点为A ,B ,C ,将△ABC向右平移m( )个单位后,△ABC某一边的中点恰好落在反比例函数 的图象上,则m的值为.15. 如图,一次函数y=﹣x+b与反比例函数y= (x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.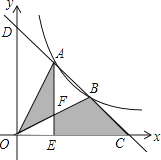 (1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .16. 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)、k的值是;(2)、如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y= 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是 .
(1)、b=(用含m的代数式表示);(2)、若S△OAF+S四边形EFBC=4,则m的值是 .16. 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)、k的值是;(2)、如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y= 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是 .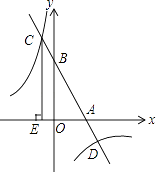 17. 如图,在平面直角坐标系中,经过点A的双曲线y= (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为 ,∠AOB=∠OBA=45°,则k的值为 .
17. 如图,在平面直角坐标系中,经过点A的双曲线y= (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为 ,∠AOB=∠OBA=45°,则k的值为 .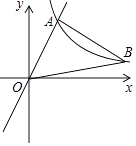 18. 如图,已知菱形 的对角线相交于坐标原点O,四个顶点分别在双曲线 和 上, .平行于x轴的直线与两双曲线分别交于点E,F,连接 , ,则 的面积为.
18. 如图,已知菱形 的对角线相交于坐标原点O,四个顶点分别在双曲线 和 上, .平行于x轴的直线与两双曲线分别交于点E,F,连接 , ,则 的面积为. 19. 如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2 ,点D为AC与反比例函数y= 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 .
19. 如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2 ,点D为AC与反比例函数y= 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 . 20. 如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
20. 如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:① = ;
②阴影部分面积是 (k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.

其中正确的结论是(把所有正确的结论的序号都填上).
三、综合题
-
21. 已知一次函数 和反比例函数 .
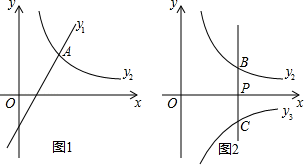 (1)、如图1,若 ,且函数 、 的图象都经过点 .
(1)、如图1,若 ,且函数 、 的图象都经过点 .①求 , 的值;
②直接写出当 时 的范围;
(2)、如图2,过点 作 轴的平行线 与函数 的图象相交于点 ,与反比例函数 的图象相交于点 .①若 ,直线 与函数 的图象相交点 .当点 、 、 中的一点到另外两点的距离相等时,求 的值;
②过点 作 轴的平行线与函数 的图象相交于点 .当 的值取不大于1的任意实数时,点 、 间的距离与点 、 间的距离之和 始终是一个定值.求此时 的值及定值 .
22. 如图1,一次函数y=﹣x+b与反比例函数y= (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数y= (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.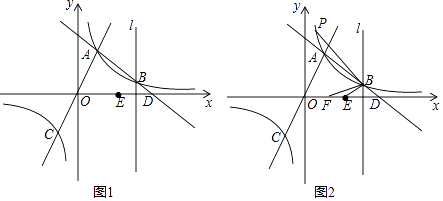 (1)、k=;(2)、判断点B,E,C是否在同一条直线上,并说明理由;(3)、如图2,已知点F在x轴正半轴上,OF= ,点P是反比例函数y= (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).23. 如图,在平面直角坐标系中,正次边形ABCDEF的对称中心P在反比例函数y= (k>0,x>0)的图象上,边CD在x轴上,点B在y轴上,已知CD=2.
(1)、k=;(2)、判断点B,E,C是否在同一条直线上,并说明理由;(3)、如图2,已知点F在x轴正半轴上,OF= ,点P是反比例函数y= (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).23. 如图,在平面直角坐标系中,正次边形ABCDEF的对称中心P在反比例函数y= (k>0,x>0)的图象上,边CD在x轴上,点B在y轴上,已知CD=2.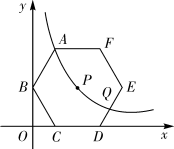 (1)、点A是否在该反比例函数的图象上?请说明理曲。(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标。(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程。24. 如图,点P是反比例函数y= (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= .
(1)、点A是否在该反比例函数的图象上?请说明理曲。(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标。(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程。24. 如图,点P是反比例函数y= (k<0)图象上的点,PA垂直x轴于点A(﹣1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= . (1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .25. 如图,反比例函数y= 的图象经过点(﹣1,﹣2 ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.
(1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是 .25. 如图,反比例函数y= 的图象经过点(﹣1,﹣2 ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP. (1)、k的值为 .(2)、在点A运动过程中,当BP平分∠ABC时,点C的坐标是 .26.
(1)、k的值为 .(2)、在点A运动过程中,当BP平分∠ABC时,点C的坐标是 .26.【合作学习】

如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数y= (k≠0)的图象分别相交于点E,F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
①该反比例函数的解析式是什么?
②当四边形AEGF为正方形时,点F的坐标是多少?
(1)、阅读合作学习内容,请解答其中的问题;(2)、小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
27. 如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB= ,反比例函数y= (k>0)在第一象限内的图象经过点A,与BC交于点F. (1)、若OA=10,求反比例函数解析式;(2)、若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;(3)、在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.28. 如图,点P为函数y= x+1与函数y= (x>0)图象的交点,点P的纵坐标为4,PB⊥x轴,垂足为点B .
(1)、若OA=10,求反比例函数解析式;(2)、若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;(3)、在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.28. 如图,点P为函数y= x+1与函数y= (x>0)图象的交点,点P的纵坐标为4,PB⊥x轴,垂足为点B . (1)、求m的值;(2)、点M是函数y= (x>0)图象上一动点,过点M作MD⊥BP于点D , 若tan∠PMD= ,求点M的坐标.29. 定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
(1)、求m的值;(2)、点M是函数y= (x>0)图象上一动点,过点M作MD⊥BP于点D , 若tan∠PMD= ,求点M的坐标.29. 定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y= (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
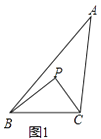 (1)、如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ,3),点N的坐标是( ,0)时,求点P的坐标;
(1)、如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ,3),点N的坐标是( ,0)时,求点P的坐标;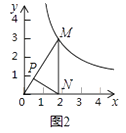 (2)、如图3,当点M的坐标是(3, ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
(2)、如图3,当点M的坐标是(3, ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;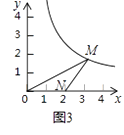 (3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.30. 有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= x与y= (k≠0)的图象性质.
(3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.30. 有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= x与y= (k≠0)的图象性质.小明根据学习函数的经验,对函数y= x与y= ,当k>0时的图象性质进行了探究.
下面是小明的探究过程:
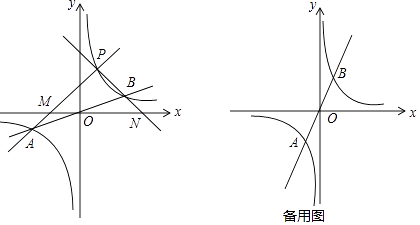 (1)、如图所示,设函数y= x与y= 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;(2)、若点P为第一象限内双曲线上不同于点B的任意一点.
(1)、如图所示,设函数y= x与y= 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;(2)、若点P为第一象限内双曲线上不同于点B的任意一点.①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ),直线PA的解析式为y=ax+b(a≠0).
则 ,
解得
∴直线PA的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.
31. 如图,一次函数y=kx+b与反比例函数y= 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.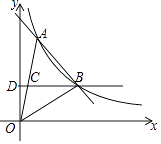 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积.32. 如图,直线 与反比例函数 的图象交于A,B两点,已知点A的坐标为 , 的面积为8.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积.32. 如图,直线 与反比例函数 的图象交于A,B两点,已知点A的坐标为 , 的面积为8. (1)、填空:反比例函数的关系式为;(2)、求直线 的函数关系式;(3)、动点P在y轴上运动,当线段 与 之差最大时,求点P的坐标.33. 如图,直线y=2x+4与反比例函数y= 的图象相交于A(﹣3,a)和B两点
(1)、填空:反比例函数的关系式为;(2)、求直线 的函数关系式;(3)、动点P在y轴上运动,当线段 与 之差最大时,求点P的坐标.33. 如图,直线y=2x+4与反比例函数y= 的图象相交于A(﹣3,a)和B两点 (1)、求k的值;(2)、直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;(3)、直接写出不等式 >x的解集.34. 如图,已知函数 的图象与一次函数 的图象相交不同的点A、B,过点A作AD⊥ 轴于点D,连接AO,其中点A的横坐标为 ,△AOD的面积为2.
(1)、求k的值;(2)、直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;(3)、直接写出不等式 >x的解集.34. 如图,已知函数 的图象与一次函数 的图象相交不同的点A、B,过点A作AD⊥ 轴于点D,连接AO,其中点A的横坐标为 ,△AOD的面积为2. (1)、求 的值及 =4时 的值;(2)、记 表示为不超过 的最大整数,例如: , ,设 ,若 ,求 值35. 如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.
(1)、求 的值及 =4时 的值;(2)、记 表示为不超过 的最大整数,例如: , ,设 ,若 ,求 值35. 如图,一次函数y=k1x+5(k1<0)的图象与坐标轴交于A,B两点,与反比例函数y= (k2>0)的图象交于M,N两点,过点M作MC⊥y轴于点C,已知CM=1.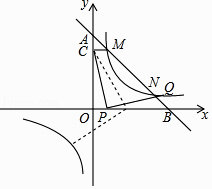 (1)、求k2﹣k1的值;(2)、若 = ,求反比例函数的解析式;(3)、在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.36. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= .
(1)、求k2﹣k1的值;(2)、若 = ,求反比例函数的解析式;(3)、在(2)的条件下,设点P是x轴(除原点O外)上一点,将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由.36. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= . (1)、求反比例函数的解析式;(2)、连接OB,求△AOB的面积.37. 如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO= ,OB=4,OE=2.
(1)、求反比例函数的解析式;(2)、连接OB,求△AOB的面积.37. 如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO= ,OB=4,OE=2. (1)、求一次函数的解析式和反比例函数的解析式;(2)、求△OCD的面积;(3)、根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.38. 如图,设反比例函数的解析式为y= (k>0).
(1)、求一次函数的解析式和反比例函数的解析式;(2)、求△OCD的面积;(3)、根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.38. 如图,设反比例函数的解析式为y= (k>0).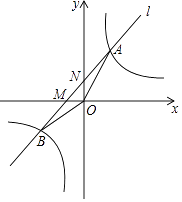 (1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.
(1)、若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;(2)、若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.