全国历年中考数学真题精选汇编:反比例函数1
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
1. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、2. 若点 , , 在反比例函数 的图像上,则 , , 的大小关系是( )A、 B、 C、 D、3. 若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y3<y2 B、y1<y2<y3 C、y3<y2<y1 D、y2<y1<y34. 已知点 在反比例函数 的图象上.若 ,则( )A、 B、 C、 D、5. 已知三个点(x1 , y1),(x2 , y2),(x3 , y3)在反比例函数y= 的图象上,其中x1<x2<0<x3 , 下列结论中正确的是( )A、y2<y1<0<y3 B、y1<y2<0<y3 C、y3<0<y2<y1 D、y3<0<y1<y26. 已知点(-2,a),(2,b),(3,c)在函数 的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a7. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A、 B、 C、 D、8. 已知双曲线 过点(3, )、(1, )、(-2, ),则下列结论正确的是( )A、 B、 C、 D、9. 反比例函数 与一次函数 的图形有一个交点 ,则k的值为( )A、1 B、2 C、 D、10. 若 、 都在函数 的图象上,且 ,则( )A、 B、 C、 D、11.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数y= (x>0)的图象与△ABC有公共点,则k的取值范围是( )
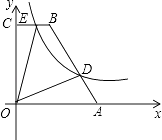
 A、2≤k≤9 B、2≤k≤8 C、2≤k≤5 D、5≤k≤812. 反比例函数y=﹣ 的图象上有P1(x1 , ﹣2),P2(x2 , ﹣3)两点,则x1与x2的大小关系是( )A、x1>x2 B、x1=x2 C、x1<x2 D、不确定13. 若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y= (k<0)上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y214. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、
A、2≤k≤9 B、2≤k≤8 C、2≤k≤5 D、5≤k≤812. 反比例函数y=﹣ 的图象上有P1(x1 , ﹣2),P2(x2 , ﹣3)两点,则x1与x2的大小关系是( )A、x1>x2 B、x1=x2 C、x1<x2 D、不确定13. 若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y= (k<0)上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y214. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、二、填空题
-
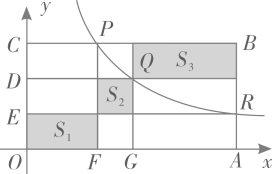
15. 点P,Q,R在反比例函数y= (常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1 , S2 , S3;若OE=ED=DC,S1+S3=27,则S2的值为。
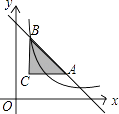
 16. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =.
16. 如图,点A、B在反比例函数 的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则 =. 17. 如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为.
17. 如图,点A在反比例函数y= (x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若 = ,△AOB的面积为6,则k的值为.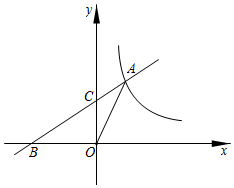 18. 将双曲线y= 向右平移1个单位长度,再向下平移2个单位长度,得到的新双曲线与直线y=kx﹣2﹣k(k>0)相交于两点,其中一个点的横坐标为a,另一个点的纵坐标为b,则(a﹣1)(b+2)=.19. 已知点 、 都在反比例函数 的图象上,则 .(填“>”或“<”)20. 如图,一次函数 的图象与x轴和y轴分别交于点A和点B与反比例函数 上的图象在第一象限内交于点 轴, 轴,垂足分别为点 ,当矩形 与 的面积相等时,k的值为 .
18. 将双曲线y= 向右平移1个单位长度,再向下平移2个单位长度,得到的新双曲线与直线y=kx﹣2﹣k(k>0)相交于两点,其中一个点的横坐标为a,另一个点的纵坐标为b,则(a﹣1)(b+2)=.19. 已知点 、 都在反比例函数 的图象上,则 .(填“>”或“<”)20. 如图,一次函数 的图象与x轴和y轴分别交于点A和点B与反比例函数 上的图象在第一象限内交于点 轴, 轴,垂足分别为点 ,当矩形 与 的面积相等时,k的值为 .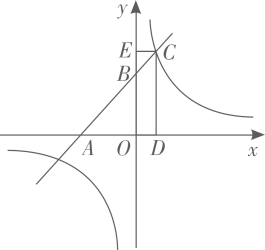 21. 如图,菱形ABCD顶点A在例函数y= (x>0)的图象上,函数 y= (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为.
21. 如图,菱形ABCD顶点A在例函数y= (x>0)的图象上,函数 y= (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为.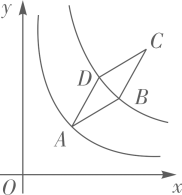 22. 已知矩形ABCD的四个顶点均在反比例函数y= 的图象上,且点A的横坐标是2,则矩形ABCD的面积为 .23.
22. 已知矩形ABCD的四个顶点均在反比例函数y= 的图象上,且点A的横坐标是2,则矩形ABCD的面积为 .23.如图,点A、B是双曲线y= 上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为
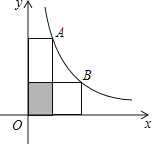 24. 若正比例函数 的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为 .25. 如图,点A是反比例函数 图象上的一点, 垂直于x轴,垂足为B. 的面积为6.若点 也在此函数的图象上,则 .
24. 若正比例函数 的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为 .25. 如图,点A是反比例函数 图象上的一点, 垂直于x轴,垂足为B. 的面积为6.若点 也在此函数的图象上,则 .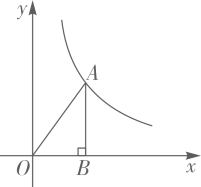 26. 如图,反比例函数 与一次函数 在第三象限交于点 .点 的坐标为(一3,0),点 是 轴左侧的一点.若以 为顶点的四边形为平行四边形.则点 的坐标为.
26. 如图,反比例函数 与一次函数 在第三象限交于点 .点 的坐标为(一3,0),点 是 轴左侧的一点.若以 为顶点的四边形为平行四边形.则点 的坐标为.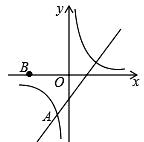 27. 如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1 , △COE的面积为S2 , 当S1>S2时,点P的横坐标x的取值范围为 .
27. 如图,直线AB与双曲线y= (k<0)交于点A,B,点P是直线AB上一动点,且点P在第二象限.连接PO并延长交双曲线于点C.过点P作PD⊥y轴,垂足为点D.过点C作CE⊥x轴,垂足为E.若点A的坐标为(﹣2,3),点B的坐标为(m,1),设△POD的面积为S1 , △COE的面积为S2 , 当S1>S2时,点P的横坐标x的取值范围为 .
三、解答题
-
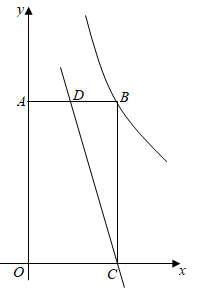
28. 如图,在平面直角坐标系中.四边形 为矩形,点 、 分别在 轴和 轴的正半轴上,点 为 的中点已知实数 ,一次函数 的图象经过点 、 ,反比例函数 的图象经过点 ,求 的值.
四、综合题
-
29. 如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y= (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
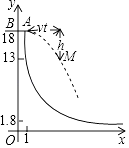 (1)、求k,并用t表示h;(2)、设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;(3)、若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
(1)、求k,并用t表示h;(2)、设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;(3)、若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
30. 在直角坐标系中,设函数 ( 是常数, , )与函数 ( 是常数, )的图象交于点A,点A关于 轴的对称点为点B。 (1)、若点B的坐标为(-1,2),
(1)、若点B的坐标为(-1,2),①求 , 的值; ②当 时,直接写出 的取值范围;
(2)、若点B在函数 ( 是常数, )的图象上,求 的值。31. 小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当. 当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系. 完成第3次训练所需时间为400秒.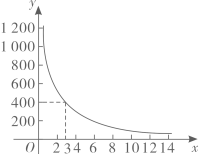 (1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.32. 经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表。
(1)、求y与x之间的函数关系式;(2)、当x的值为6,8,10时,对应的函数值分别为y1 , y2 , y3 , 比较(y1-y2)与(y2-y3)的大小: y1-y2y2-y3.32. 经过实验获得两个变量x(x>0),y(y>0)的一组对应值如下表。x
1
2
3
4
5
6
y
6
2.9
2
1.5
1.2
1
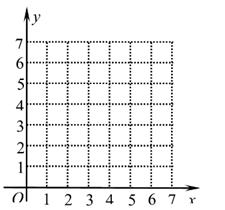 (1)、请画出相应函数的图象,并求出函数表达式。(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上。若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由。33. 设函数y1= ,y2=- (k>0)。(1)、当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a-4,求a和k的值。(2)、设m≠0,且m≠-1,当x=m时,y1=p;当x=m+1时,y1=q。圆圆说:“p一定大于q”。你认为圆圆的说法正确吗?为什么?34. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)、请画出相应函数的图象,并求出函数表达式。(2)、点A(x1 , y1),B(x2 , y2)在此函数图象上。若x1<x2 , 则y1 , y2有怎样的大小关系?请说明理由。33. 设函数y1= ,y2=- (k>0)。(1)、当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a-4,求a和k的值。(2)、设m≠0,且m≠-1,当x=m时,y1=p;当x=m+1时,y1=q。圆圆说:“p一定大于q”。你认为圆圆的说法正确吗?为什么?34. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.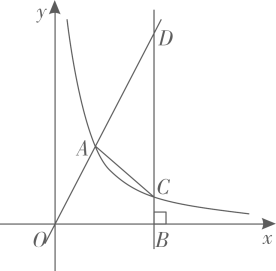 (1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.35. 已知正比例函数y=kx(k≠0)与反比例函数 的图像都经过点A(m,2).
(1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.35. 已知正比例函数y=kx(k≠0)与反比例函数 的图像都经过点A(m,2).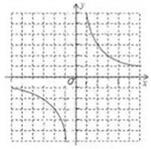 (1)、求k,m的值;(2)、在图中画出正比例函数y=kx的图像,并根据图像,写出正比例函数值大于反比例函数值时x的取值范围.36. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位: )是反比例函数关系.当 时, .(1)、写出I关于R的函数解析式;(2)、完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
(1)、求k,m的值;(2)、在图中画出正比例函数y=kx的图像,并根据图像,写出正比例函数值大于反比例函数值时x的取值范围.36. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位: )是反比例函数关系.当 时, .(1)、写出I关于R的函数解析式;(2)、完成下表,并在给定的平面直角坐标系中画出这个函数的图象;…
…
…
…
 (3)、如果以此蓄电池为电源的用电器的限制电流不能超过 .那么用电器可变电阻应控制在什么范围内?37. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
(3)、如果以此蓄电池为电源的用电器的限制电流不能超过 .那么用电器可变电阻应控制在什么范围内?37. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0. (1)、当y1﹣y2=4时,求m的值;
(1)、当y1﹣y2=4时,求m的值;
(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).
38. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: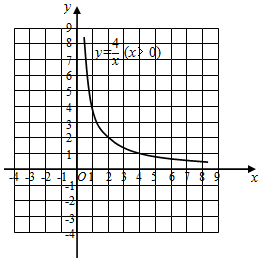 (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为m,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,周长m的值为;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为.
-