全国历年中考数学真题精选汇编:一次函数2
试卷更新日期:2021-07-08 类型:二轮复习
一、单选题
-
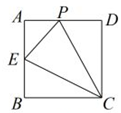
1. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
 A、
A、 B、
B、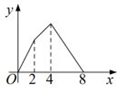 C、
C、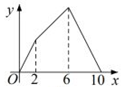 D、
D、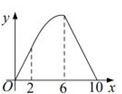 2. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
2. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A、7:20 B、7:30 C、7:45 D、7:503. 过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )A、(4, ) B、(4,3) C、(5, ) D、(5,3)4. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( ) A、12 B、8 C、10 D、135. 如图,在平面直角坐标系中,点 在x轴正半轴上,点 在直线 上,若 ,且 均为等边三角形,则线段 的长度为( )
A、12 B、8 C、10 D、135. 如图,在平面直角坐标系中,点 在x轴正半轴上,点 在直线 上,若 ,且 均为等边三角形,则线段 的长度为( )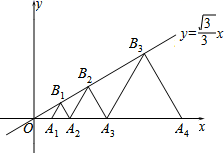 A、 B、 C、 D、6. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:
A、 B、 C、 D、6. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;
②乙行走的速度是甲的1.5倍;
③b=960;
④a=34.
以上结论正确的有( )
 A、①② B、①②③ C、①③④ D、①②④
A、①② B、①②③ C、①③④ D、①②④二、填空题
-
7. 元朝朱世杰的《算学启蒙》一书记载:“今有良马目行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之,”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是 .
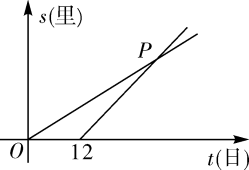 8. 如图,在平面直角坐标系 中,半径为2的 与 轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为.
8. 如图,在平面直角坐标系 中,半径为2的 与 轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为. 9. 在平面直角坐标系中,直线 与 轴交于点 ,如图所示,依次作正方形 ,正方形 ,正方形 ,正方形 ,…,点 , , , ,…在直线 上,点 , , , ,…在 轴正半轴上,则前 个正方形对角线的和是.
9. 在平面直角坐标系中,直线 与 轴交于点 ,如图所示,依次作正方形 ,正方形 ,正方形 ,正方形 ,…,点 , , , ,…在直线 上,点 , , , ,…在 轴正半轴上,则前 个正方形对角线的和是.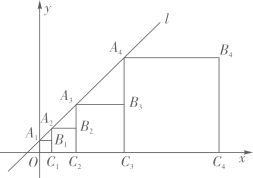 10. 如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2 , 使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3 , 使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4 , Rt△OA4A5 , …,Rt△OA2016A2017 , 若点A0(1,0),则点A2017的横坐标为 .
10. 如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2 , 使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3 , 使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4 , Rt△OA4A5 , …,Rt△OA2016A2017 , 若点A0(1,0),则点A2017的横坐标为 .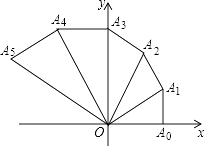
三、综合题
-
11. 方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
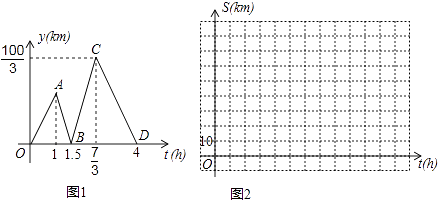 (1)、分别求出线段BC,CD所在直线的函数表达式;(2)、当20<y<30时,求t的取值范围;(3)、分别求出甲,乙行驶的路程S甲 , S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;(4)、丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过 h与乙相遇,问丙出发后多少时间与甲相遇?12. 如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 .
(1)、分别求出线段BC,CD所在直线的函数表达式;(2)、当20<y<30时,求t的取值范围;(3)、分别求出甲,乙行驶的路程S甲 , S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;(4)、丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过 h与乙相遇,问丙出发后多少时间与甲相遇?12. 如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 .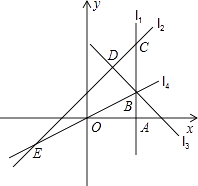 (1)、若点B在线段AC上,且S1=S2 , 则B点坐标为;(2)、若点B在直线l1上,且S2= S1 , 则∠BOA的度数为 .13. 如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点 .甲从中山路上点 出发,骑车向北匀速直行;与此同时,乙从点 出发,沿北京路步行向东匀速直行.设出发 时,甲、乙两人与点 的距离分别为 、 .已知 、 与 之间的函数关系如图②所示.
(1)、若点B在线段AC上,且S1=S2 , 则B点坐标为;(2)、若点B在直线l1上,且S2= S1 , 则∠BOA的度数为 .13. 如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点 .甲从中山路上点 出发,骑车向北匀速直行;与此同时,乙从点 出发,沿北京路步行向东匀速直行.设出发 时,甲、乙两人与点 的距离分别为 、 .已知 、 与 之间的函数关系如图②所示.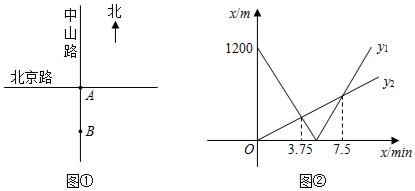 (1)、求甲、乙两人的速度;(2)、当 取何值时,甲、乙两人之间的距离最短?14. 某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.(1)、若基地一天的总销售收入为y元,求y与x的函数关系式;(2)、试求如何分配工人,才能使一天的销售收入最大?并求出最大值.15. 平面直角坐标系xOy中,点A,B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A,B,且a、m满足2a﹣m=d(d为常数).(1)、若一次函数y1=kx+b的图象经过A、B两点.
(1)、求甲、乙两人的速度;(2)、当 取何值时,甲、乙两人之间的距离最短?14. 某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤,设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.(1)、若基地一天的总销售收入为y元,求y与x的函数关系式;(2)、试求如何分配工人,才能使一天的销售收入最大?并求出最大值.15. 平面直角坐标系xOy中,点A,B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A,B,且a、m满足2a﹣m=d(d为常数).(1)、若一次函数y1=kx+b的图象经过A、B两点.①当a=1、d=﹣1时,求k的值;
②若y1随x的增大而减小,求d的取值范围;
(2)、当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;(3)、点A,B的位置随着a的变化而变化,设点A,B运动的路线与y轴分别相交于点C,D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.16. 操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.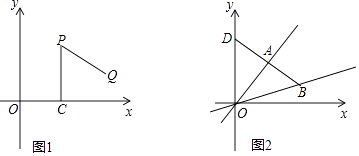 (1)、点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣ ),则点M的坐标为 .(2)、A是函数y= x图象上异于原点O的任意一点,经过T变换后得到点B.
(1)、点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,﹣ ),则点M的坐标为 .(2)、A是函数y= x图象上异于原点O的任意一点,经过T变换后得到点B.①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
17. 科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程:①在科研所到宿舍楼之间修一条笔直的道路;②对宿舍楼进行防辐射处理,已知防辐射费y万元与科研所到宿舍楼的距离xkm之间的关系式为y=ax+b(0≤x≤9).当科研所到宿舍楼的距离为1km时,防辐射费用为720万元;当科研所到宿舍楼的距离为9km或大于9km时,辐射影响忽略不计,不进行防辐射处理.设每公里修路的费用为m万元,配套工程费w=防辐射费+修路费.
(1)、当科研所到宿舍楼的距离x=9km时,防辐射费y=万元,a= , b=(2)、若每公里修路的费用为90万元,求当科研所到宿舍楼的距离为多少km时,配套工程费最少?(3)、如果配套工程费不超过675万元,且科研所到宿舍楼的距离小于9km,求每公里修路费用m万元的最大值.18. 已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2 .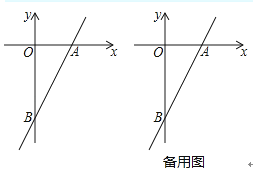 (1)、当P为线段AB的中点时,求d1+d2的值。
(1)、当P为线段AB的中点时,求d1+d2的值。
(2)、直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标。
(3)、若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值。
19. 阅读材料:在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= .
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= = .
根据以上材料,解决下列问题:
(1)、点P1(3,4)到直线y=﹣ x+ 的距离为;(2)、已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ x+b相切,求实数b的值;(3)、如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.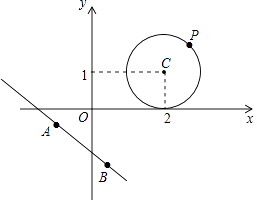 20. 如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ x﹣ 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
20. 如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ x﹣ 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.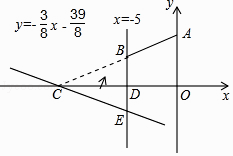 (1)、求点C,E的坐标及直线AB的解析式;(2)、设面积的和S=S△CDE+S四边形ABDO , 求S的值;(3)、在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.21. 某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
(1)、求点C,E的坐标及直线AB的解析式;(2)、设面积的和S=S△CDE+S四边形ABDO , 求S的值;(3)、在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.21. 某商店能过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:第1个
第2个
第3个
第4个
…
第n个
调整前单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后单价x(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)、求y与x的函数关系式,并确定x的取值范围;(2)、某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?(3)、这n个玩具调整前、后的平均单价分别为 , ,猜想 与 的关系式,并写出推导出过.22. 用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)、根据题意,填写下表:一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
0.5
2
…
乙复印店收费(元)
0.6
2.4
…
(2)、设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1 , y2关于x的函数关系式;(3)、当x>70时,顾客在哪家复印店复印花费少?请说明理由.23. 如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同) (1)、填空:BC的长是;(2)、求S关于x的函数关系式,并写出x的取值范围.24. 如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
(1)、填空:BC的长是;(2)、求S关于x的函数关系式,并写出x的取值范围.24. 如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).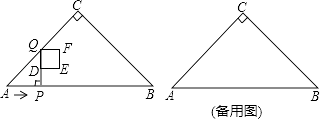 (1)、当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);(2)、当点P不与点B重合时,求点F落在边BC上时x的值;(3)、当0<x<2时,求y关于x的函数解析式;
(1)、当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);(2)、当点P不与点B重合时,求点F落在边BC上时x的值;(3)、当0<x<2时,求y关于x的函数解析式;
(4)、直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.25. 如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.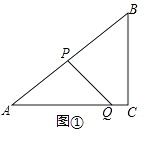 (1)、求线段AQ的长;(用含t的代数式表示)(2)、连结PQ,当PQ与△ABC的一边平行时,求t的值;(3)、如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
(1)、求线段AQ的长;(用含t的代数式表示)(2)、连结PQ,当PQ与△ABC的一边平行时,求t的值;(3)、如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.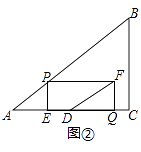 26. 深圳某科技公司在甲地、乙地分别生产了17台、15台同一种型号的检测设备,全部运往大运赛场A、B两馆,其中运往A馆18台、运往B馆14台;运往A、B两馆的运费如表1:
26. 深圳某科技公司在甲地、乙地分别生产了17台、15台同一种型号的检测设备,全部运往大运赛场A、B两馆,其中运往A馆18台、运往B馆14台;运往A、B两馆的运费如表1:表 1
出发地
目的地
甲地
乙地
A馆
800元/台
700元/台
B馆
500元/台
600元/台
表 2
出发地
目的地
甲地
乙地
A馆
x台
(台)
B馆
(台)
(台)
(1)、设甲地运往A馆的设备有x台,请填写表2,并求出总运费元y(元)与x (台) 的函数关系式;(2)、要使总运费不高于20200元,请你帮助该公司设计调配方案,并写出有哪几种方案;(3)、当x为多少时,总运费最小,最小值是多少?