全国历年中考数学真题精选汇编:方程与不等式2
试卷更新日期:2021-07-07 类型:二轮复习
一、单选题
-
1. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为 株,则正确的方程是( )A、 B、 C、 D、2. 已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )A、1一定不是关于x的方程x2+bx+a=0的根 B、0一定不是关于x的方程x2+bx+a=0的根 C、1和﹣1都是关于x的方程x2+bx+a=0的根 D、1和﹣1不都是关于x的方程x2+bx+a=0的根3. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )A、 B、 C、 D、4. 不等式组: 的解集是( )A、﹣3<x≤2 B、﹣3≤x<2 C、x≥2 D、x<﹣35. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 = B、 = C、 = D、 =6. 不等式1+x<0的解集在数轴上表示正确的是( )A、
 B、
B、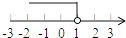 C、
C、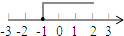 D、
D、 7. 对于两个不相等的实数a、b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,﹣x}=的解为( )A、1- B、2- C、1+或1- D、1+或﹣18. 抛物线 的对称轴为直线 .若关于 的一元二次方程 ( 为实数)在 的范围内有实数根,则 的取值范围是( )A、 B、 C、 D、
7. 对于两个不相等的实数a、b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,﹣x}=的解为( )A、1- B、2- C、1+或1- D、1+或﹣18. 抛物线 的对称轴为直线 .若关于 的一元二次方程 ( 为实数)在 的范围内有实数根,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 不等式组 的解集为 .
三、计算题
-
10. (1)计算:|﹣4|+23+3×(﹣5)
(2)解方程组:
11. 先化简,再求值: ,其中 为整数且满足不等式组四、解答题
-
12. 《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
13. 解不等式组: 并写出它的整数解.14. 自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
a
b
1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数
0
1
2
3
4
5
人数
5
15
10
30
25
15
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
15. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:“有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?”试用列方程(组)解应用题的方法求出问题的解.16. 有甲、乙两种车辆参加来宾市“桂中水城”建设工程挖渠运土,已知5辆甲种车和4辆乙种车一次可运土共140立方米,3辆甲种车和2辆乙种车一次可运土共76立方米.求甲、乙两种车每辆一次可分别运土多少立方米?17. 已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为N.
(ⅰ)若﹣1≤a≤﹣ ,求线段MN长度的取值范围;
(ⅱ)求△QMN面积的最小值.
18. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批淡水鱼放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知: 与 的函数关系为 ; 与 的函数关系如图所示.
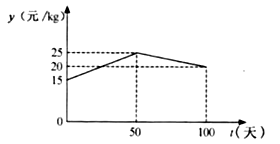
①分别求出当 和 时, 与 的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为 元,求当 为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
19.如图,某日的钱塘江观潮信息如表:

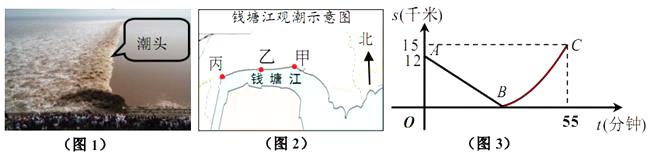
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 (千米)与时间 (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ,点 坐标为 ,曲线 可用二次函数 ( , 是常数)刻画.
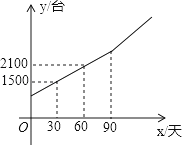
(1)、求 的值,并求出潮头从甲地到乙地的速度;(2)、11:59时,小红骑单车从乙地出发,沿江边公路以 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?(3)、相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 , 是加速前的速度).20.随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
 21.
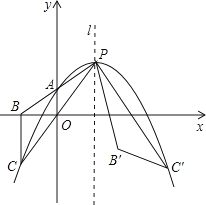
21.如图,抛物线y=a(x﹣m)2+2m﹣2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m﹣1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
(1)该抛物线的解析式为 (用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
 22. 楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
22. 楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
五、综合题
-
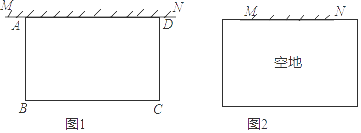
23. 某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.(1)、求该车间的日废水处理量m;(2)、为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.24. 空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
 (1)、已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.
(1)、已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)、已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
25. 如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏. (1)、若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;(2)、求矩形菜园ABCD面积的最大值.26. 现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)、求A,B两种商品每件各是多少元?(2)、如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?27.
(1)、若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;(2)、求矩形菜园ABCD面积的最大值.26. 现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.(1)、求A,B两种商品每件各是多少元?(2)、如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?27. (1)、如图,AB平分∠CAD,AC=AD,求证:BC=BD;(2)、列方程解应用题
(1)、如图,AB平分∠CAD,AC=AD,求证:BC=BD;(2)、列方程解应用题把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本,这个班有多少学生?
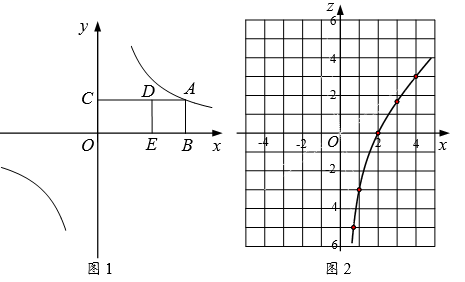
28. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?29. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?30. 背景:点A在反比例函数 的图象上, 轴于点B, 轴于点C,分别在射线 上取点 ,使得四边形 为正方形.如图1,点A在第一象限内,当 时,小李测得 .探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
 (1)、求k的值.(2)、设点 的横坐标分别为 ,将z关于x的函数称为“Z函数”.如图2,小李画出了 时“Z函数”的图象.
(1)、求k的值.(2)、设点 的横坐标分别为 ,将z关于x的函数称为“Z函数”.如图2,小李画出了 时“Z函数”的图象.①求这个“Z函数”的表达式.
②补画 时“Z函数”的图象,并写出这个函数的性质(两条即可).
③过点 作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
31.小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
 (1)、若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;(2)、若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
(1)、若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;(2)、若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
32. 某镇水库的可用水量为12000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.(1)、问:年降水量为多少万立方米?每人年平均用水量多少立方米?(2)、政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标?33. 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:y= .
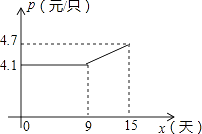 (1)、李明第几天生产的粽子数量为420只?(2)、如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)(3)、设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?34. 八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
(1)、李明第几天生产的粽子数量为420只?(2)、如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)(3)、设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?34. 八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表参赛同学
答对题数
答错题数
未答题数
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
(1)、根据以上信息,求A,B,C,D四位同学成绩的平均分;(2)、最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
35. 小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索.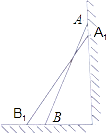
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)、请你将小明对“思考题”的解答补充完整:解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1= ﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由 得方程 ,
解方程得x1= , x2= ,
∴点B将向外移动米.
(2)、解完“思考题”后,小聪提出了如下两个问题:【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
36. 学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.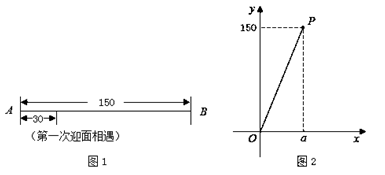 (1)、【观察】
(1)、【观察】①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)、【发现】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① =;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)、【拓展】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是.(直接写出结果)
37. 如图①,直线l表示一条东西走向的笔直公路,四边形ABCD是一块边长为100米的正方形草地,点A,D在直线l上,小明从点A出发,沿公路l向西走了若干米后到达点E处,然后转身沿射线EB方向走到点F处,接着又改变方向沿射线FC方向走到公路l上的点G处,最后沿公路l回到点A处.设AE=x米(其中x>0),GA=y米,已知y与x之间的函数关系如图②所示,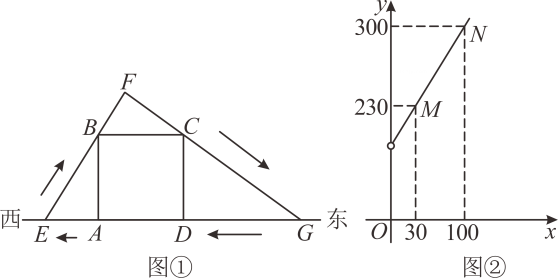 (1)、求图②中线设线段MN所在直线的函数表达式(2)、试问小明从起点A出发直至最后回到点A处,所走过的路径(即△EFG)是否可以是一个等腰三角形?如果可以,求出相应x的值;如果不可以,说明理由.38. 网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中 ).
(1)、求图②中线设线段MN所在直线的函数表达式(2)、试问小明从起点A出发直至最后回到点A处,所走过的路径(即△EFG)是否可以是一个等腰三角形?如果可以,求出相应x的值;如果不可以,说明理由.38. 网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中 ).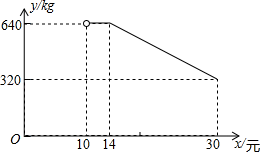 (1)、直接写出y与x之间的函数关系式及自变量的取值范围.(2)、若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?(3)、设每天销售该特产的利润为W元,若 ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?39. 为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次;若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费x元(为便于结算,停车费x只取整数),此停车场的日净收入为y元(日净收入=每天共收停车费﹣每天固定的支出)回答下列问题:(1)、①当x≤10时,y与x的关系式为:;
(1)、直接写出y与x之间的函数关系式及自变量的取值范围.(2)、若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?(3)、设每天销售该特产的利润为W元,若 ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?39. 为解决消费者停车难的问题,某商场新建一小型轿车停车场,经测算,此停车场每天需固定支出的费用(包括设施维修费、管理人员工资等)为600元,为制定合理的收费标准,该商场对每天轿车停放辆次(每辆轿车每停放一次简称为“辆次”)与每辆轿车的收费情况进行调查,发现每辆次轿车的停车费定价不超过10元时,每天来此停放的轿车都为300辆次;若每辆次轿车的停车费定价超过10元,则每超过1元,每天来此停放的轿车就减少12辆次,设每辆次轿车的停车费x元(为便于结算,停车费x只取整数),此停车场的日净收入为y元(日净收入=每天共收停车费﹣每天固定的支出)回答下列问题:(1)、①当x≤10时,y与x的关系式为:;②当x>10时,y与x的关系式为:;
(2)、停车场能否实现3000元的日净收入?如能实现,求出每辆次轿车的停车费定价,如不能实现,请说明理由;(3)、该商场要求此停车场既要吸引顾客,使每天轿车停放的辆次较多,又要有最大的日净收入,按此要求,每辆次轿车的停车费定价应定为多少元?此时最大日净收入是多少元?40. 2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程约为1026千米,高铁平均时速为普快平均时速的2.5倍.(1)、求高铁列车的平均时速;
(2)、某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到当日8:40从烟台至城市的高铁票,而且从该市火车站到会议地点最多需要1.5小时,试问在高铁列车准点到达的情况下他能在开会之前到达吗?
-