山东省淄博市临淄区2021年中考数学二模试卷

试卷更新日期：2021-07-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 近似数5.0×10²精确到（）

A、十分位 B、个位 C、十位 D、百位

查看试题解析
2. 2020年6月23日，中国第55颗北斗导航卫星成功发射，顺利完成全球组网．其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片，已实现规模化应用.22纳米=0.000000022米，将0.000000022用科学记数法表示为（）

A、 $2.2 \times 10^{8}$ B、 $2.2 \times 10^{- 8}$ C、 $0.22 \times 10^{- 7}$ D、 $22 \times 10^{- 9}$

查看试题解析
3. 如图，C，D是数轴上的两点，它们分别表示﹣2.4，1.6，O为原点，则线段CD的中点表示的有理数是（）

A、﹣0.4 B、﹣0.8 C、2 D、1

查看试题解析
4. 与下面科学计算器的按键顺序：

对应的计算结果是（）

A、1 B、－0.5 C、1.5 D、0.5

查看试题解析
5. 如图所示的几何体，其俯视图是（）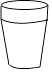

A、 B、 C、 D、

查看试题解析
6. 超市店庆促销，某种书包原价每个x元，第一次降价打“八折”，第二次降价每个又减10元，经两次降价后售价为90元，则得到方程（）

A、0.8x﹣10=90 B、0.08x﹣10=90 C、90﹣0.8x=10 D、x﹣0.8x﹣10=90

查看试题解析
7. 关于二次函数 $y = x^{2} + 2 x - 8$ ，下列说法正确的是（）

A、图象的对称轴在 $y$ 轴的右侧 B、图象与 $y$ 轴的交点坐标为 $(0, 8)$ C、图象与 $x$ 轴的交点坐标为 $(- 2, 0)$ 和 $(4, 0)$ D、 $y$ 的最小值为－9

查看试题解析
8. 如图，在 $△ A B C$ 中， $B C = 120$ ，高 $A D = 60$ ，正方形 $E F G H$ 一边在 $B C$ 上，点 $E ， F$ 分别在 $A B ， A C$ 上， $A D$ 交 $E F$ 于点 $N$ ，则 $A N$ 的长为（）

A、 $15$ B、 $20$ C、 $25$ D、 $30$

查看试题解析
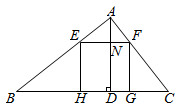9. 在如图所示的正方形网格中，点A，B，C，D，O均在格点上，则点O是（）

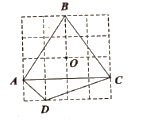A、 $△ A C D$ 的外心 B、 $△ A C D$ 的内心 C、 $△ A B C$ 的外心 D、 $△ A B C$ 的内心

查看试题解析
10. 某工程队承接了80万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了35%，结果提前40天完成了这一任务；设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（）

A、 $\frac{80 (1 + 35 %)}{x} - \frac{80}{x} = 40$ B、 $\frac{80}{(1 + 35 %) x} - \frac{80}{x} = 40$ C、 $\frac{80}{x} - \frac{80}{(1 + 35 %) x} = 40$ D、 $\frac{80}{x} - \frac{80 (1 + 35 %)}{x} = 40$

查看试题解析
11. 如图，在平行四边形ABCD中，AD＝2，AB＝ $\sqrt{6}$ ，∠B是锐角，AE⊥BC于点E ， F是AB的中点，连接DF ， EF ．若∠EFD＝90°，则线段AE的长为（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\sqrt{5}$

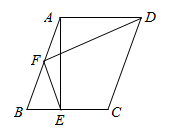查看试题解析
12. 等边三角形ABC内接于⊙O ， P是劣弧 $\overset{⌢}{A B}$ 上一点（不与A ， B重合），将△PBC绕C点顺时针旋转60° ，得△DAC ， AB交PC于点E ．则下列结论错误的是（）

A、PA＋PB＝PC B、 $B C^{2} = P C \cdot E C$ C、四边形ABCD有可能成为平行四边形 D、△PCD的面积有最大值

查看试题解析

二、填空题

13. |－6|＝．

查看试题解析
14. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：
时间（小时）
5
6
7
8
人数
10
15
20
5
则这50名学生这一周在校的平均体育锻炼时间是小时．

查看试题解析
15. 点P（a ， b）在函数y＝3x+2的图象上，则代数式6a﹣2b+1的值等于．

查看试题解析
16. 如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，以点A为圆心，1为半径作弧，分别交 AB ， AC于点D ， E ，以点C为圆心，4为半径作弧，分别交AC ， BC于点A ， F ．若图中阴影部分的面积分别为S₁ ， S₂ ，则S₁－S₂的值为．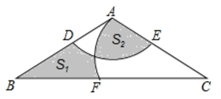

查看试题解析
17. 如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去.已知第一个矩形的面积为1，则第n个矩形的面积为.

查看试题解析

三、解答题

18. 先化简，再求值： $(x + 2 + \frac{3}{x - 2}) \div \frac{1 + 2 x + x^{2}}{x - 2}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
19. 如图

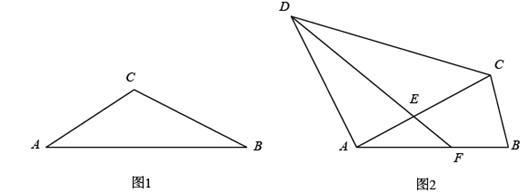(1)、已知如图1：△ABC ．求作：⊙O ，使它经过点B和点C ，并且圆心O在∠A的平分线上（保留作图痕迹）．

(2)、如图2，点F在线段AB上，AD∥BC ， AC交DF于点E ， ∠BAC＝∠ADF ， AE＝BC ．求证：△ACD是等腰三角形．

查看试题解析
20. 某校为调查学生对海洋科普知识的了解情况，从全校学生中随机抽取 $n$ 名学生进行测试，测试成绩进行整理后分成五组，并绘制成如下的频数直方图和扇形统计图．

请根据图中信息解答下列问题：

(1)、补全频数直方图；

(2)、在扇形统计图中，“70~80”这组的百分比 $m =$ ；

(3)、已知“80~90”这组的数据如下：81，83，84，85，85，86，86，86，87，88，88，89．抽取的 $n$ 名学生测试成绩的中位数是分；

(4)、若成绩达到80分以上（含80分）为优秀，请你估计全校1200名学生对海洋科普知识了解情况为优秀的学生人数．

查看试题解析
21. 随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多的进人普通家庭，成为居民消费新的增长点.据某市交通部门统计，2016年底全市汽车拥有量为15万辆，而截止到2018年底，全市的汽车拥有量已达21.6万辆.

(1)、求2016年底至2018年底该市汽车拥有量的年平均增长率；

(2)、为了保护环境，缓解汽车拥堵状况，从2019年起，该市交通部门拟控制汽车总量，要求到2020年底全市汽车拥有量不超过23.196万辆；另据估计，该市从2019年起每年报废的汽车数量是上年底汽车拥有量的10%.假定在这种情况下每年新增汽车数量相同，请你计算出该市每年新增汽车数量最多不能超过多少万辆.

查看试题解析
22. 如图， $A B$ 与 $⊙ O$ 相切于点B， $A O$ 交 $⊙ O$ 于点C， $A O$ 的延长线交 $⊙ O$ 于点D， $E$ 是 $\overset{⌢}{B C D}$ 上不与 $B ， D$ 重合的点， $\sin A = \frac{1}{2}$ ．

(1)、求 $∠ B E D$ 的大小；

(2)、若 $⊙ O$ 的半径为3，点F在 $A B$ 的延长线上，且 $B F = 3 \sqrt{3}$ ，求证： $D F$ 与 $⊙ O$ 相切．

查看试题解析
23. 如图

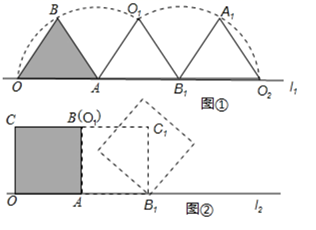
如图①，小慧同学把一个等边三角形纸片（即△OAB）放在直线l₁上，OA边与直线l₁重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O₁处，点B运动到了点B₁处；小慧又将三角形纸片AO₁B₁绕B₁点按顺时针方向旋转120°，点A运动到了点A₁处，点O₁运动到了点O₂处（即顶点O经过上述两次旋转到达O₂处）．

小慧还发现：三角形纸片在上述两次旋转过程中，顶点O运动所形成的图形是两段圆弧，即弧OO₁和弧O₁O₂ ，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧与直线l₁围成的图形面积等于扇形AOO₁的面积、△AO₁B₁的面积和扇形B₁O₁O₂的面积之和．

小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l₂上，OA边与直线l₂重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处；小慧又将正方形纸片AO₁C₁B₁绕B₁点按顺时针方向旋转90°，……，按上述方法经过若干次旋转后，她提出了如下问题：

(1)、若正方形纸片OABC按上述方法经过3次旋转，求顶点O经过的路程，并求顶点O在此运动过程中所形成的图形与直线l₂围成图形的面积；若正方形OABC按上述方法经过5次旋转，求顶点O经过的路程；

(2)、正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是 $\frac{21 + 10 \sqrt{2}}{2} π$ ？

查看试题解析
24. 如图，在平面直角坐标系中，点A（1，0），点B（0，3），点C在x轴的负半轴上，∠BCA＝45°，CD⊥AB ，垂足为点D ， CD与y轴交于点E ．点A ， B ， C分别在二次函数图象上．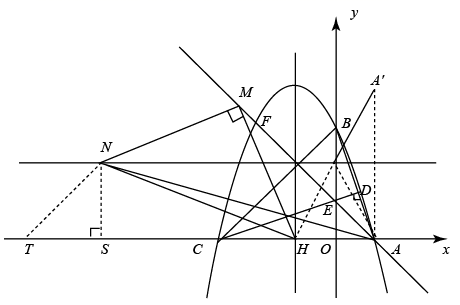

(1)、求二次函数表达式；

(2)、连接AE并延长交二次函数的图象于点F ，请你求出点F的坐标；

(3)、设二次函数的对称轴与x轴的交点为H ，在直线AF上有一动点M ，连接MH ，将线段MH 绕点M顺时针旋转90°得到线段MN ，连接HN ， AN ，求NH＋AN的最小值．

查看试题解析

时间（小时）	5	6	7	8
人数	10	15	20	5