陕西省初中数学历年真题与模拟汇编:图形的变化2
试卷更新日期:2021-07-07 类型:二轮复习
一、单选题
-
1. 如图所示的几何体,它的左视图是( )
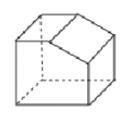 A、
A、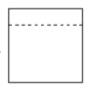 B、
B、 C、
C、 D、
D、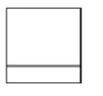 2. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
2. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )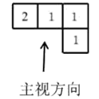 A、
A、 B、
B、 C、
C、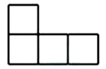 D、
D、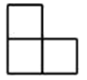 3. 如图,从左面看该几何体得到的形状是( )
3. 如图,从左面看该几何体得到的形状是( ) A、
A、 B、
B、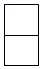 C、
C、 D、
D、 4. 下图是由四个小正方体叠成的一个立体图形,那么它的俯视图是( )
4. 下图是由四个小正方体叠成的一个立体图形,那么它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示的几何体的主视图是( )
5. 如图所示的几何体的主视图是( )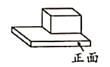 A、
A、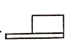 B、
B、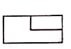 C、
C、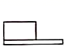 D、
D、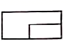 6. 物体如图,则这两个物体的俯视图应是( )
6. 物体如图,则这两个物体的俯视图应是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 一个由半球和圆柱组成的几何体如图水平放置,其俯视图为( )
7. 一个由半球和圆柱组成的几何体如图水平放置,其俯视图为( )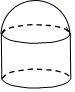 A、
A、 B、
B、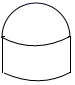 C、
C、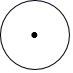 D、
D、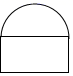 8. 如图,下面关于正六棱柱的视图(主视图、左视图、俯视图)中,画法错误的是 ( )
8. 如图,下面关于正六棱柱的视图(主视图、左视图、俯视图)中,画法错误的是 ( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( )
9. 如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( ) A、
A、 B、
B、 C、
C、 D、
D、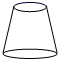 10. 发展工业是强国之梦的重要举措,如图所示零件的左视图是( )
10. 发展工业是强国之梦的重要举措,如图所示零件的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 把如图所示的几何体组合中的A正方体放到B正方体的上面,则下列说法正确的是( )
11. 把如图所示的几何体组合中的A正方体放到B正方体的上面,则下列说法正确的是( ) A、主视图不变 B、俯视图不变 C、左视图不变 D、三种视图都不变12. 如图所示的几何体的左视图是( )
A、主视图不变 B、俯视图不变 C、左视图不变 D、三种视图都不变12. 如图所示的几何体的左视图是( ) A、
A、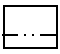 B、
B、 C、
C、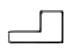 D、
D、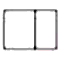 13. 如图,下面几何体由五个大小相同的小立方块组成,则它的左视图是( )
13. 如图,下面几何体由五个大小相同的小立方块组成,则它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 14. 如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE= CD,过点B作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为( )
14. 如图,∠ACB=90°,D为AB中点,连接DC并延长到点E,使CE= CD,过点B作BF∥DE交AE的延长线于点F.若BF=10,则AB的长为( ) A、12 B、10 C、8 D、515. 如图,点O为△ABC边 AC的中点,连接BO并延长到点D,连接AD、CD,若BD=12,AC=8,∠AOD=120°,则四边形ABCD的面积为( )
A、12 B、10 C、8 D、515. 如图,点O为△ABC边 AC的中点,连接BO并延长到点D,连接AD、CD,若BD=12,AC=8,∠AOD=120°,则四边形ABCD的面积为( ) A、2 B、2 C、 D、16. 如图,在△ABC中,BC=6,∠A=60°.若 O是△ABC的外接圆,则 O的半径长为( )
A、2 B、2 C、 D、16. 如图,在△ABC中,BC=6,∠A=60°.若 O是△ABC的外接圆,则 O的半径长为( )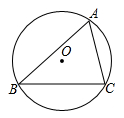 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 如图,已知 ,点 为边 中点,点 在线段 上运动,点 在线段 上运动,连接 ,则 周长的最小值为.
 18. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
18. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是. 19. 如图,在平行四边形 中, 为AD的中点,F是边AB上不与点 重合的一个动点,将 沿 折叠,得到 连接 则 周长的最小值为.
19. 如图,在平行四边形 中, 为AD的中点,F是边AB上不与点 重合的一个动点,将 沿 折叠,得到 连接 则 周长的最小值为.
三、解答题
-
20. 长安塔,又名天人长安塔,位于西安世园会园区制高点小终南山上,是西安世园会的标志,也是园区的观景塔,游人可登塔俯瞰,全园美景尽收眼底。小军利用刚学过的测量知识来测量长安塔的高度,如图所示,他和学习小组的同学带着测量工具来到长安塔前,恰好发现有一个临时搭建的台子 ,小军在台子底部 处测得塔顶 的仰角为 ,然后又到台子的顶端 处测得塔顶 的仰角为 ,已知 均垂直于 ,求长安塔的高度 .(参考数据 , )
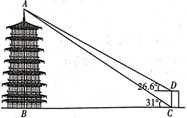 21. 在数学实践活动课上,老师带领同学们到附近的公园测量园内一古楼的高度.测量方法如下:首先,用测角仪 在C处测得楼顶端 点的仰角为 ,然后,往古楼方向前进 米至E处,测得楼顶端 点的仰角为 , .已知点B、E、C在一条直线上, , , ,测量示意图如图所示,请你求出该古楼的高度 .(参考数据: , , , , , )
21. 在数学实践活动课上,老师带领同学们到附近的公园测量园内一古楼的高度.测量方法如下:首先,用测角仪 在C处测得楼顶端 点的仰角为 ,然后,往古楼方向前进 米至E处,测得楼顶端 点的仰角为 , .已知点B、E、C在一条直线上, , , ,测量示意图如图所示,请你求出该古楼的高度 .(参考数据: , , , , , ) 22. 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709, ≈1.414.)
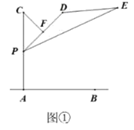
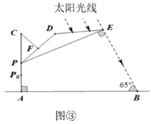
22. 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709, ≈1.414.) 23. 在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱AC直于地面AB,点P为立柱上的滑动调节点,伞体的截面示意图为 ,F为PD中点, , , .当点 位于初始位置 时,点D与C重合(如图②).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为 (如图③),为使遮阳效果最佳,点P需从 上调多少米?(结果精确到 )(参考数据: , , )
23. 在炎热的夏季,遮阳伞在我们的生活中随处可见.如图①,滑动调节式遮阳伞的立柱AC直于地面AB,点P为立柱上的滑动调节点,伞体的截面示意图为 ,F为PD中点, , , .当点 位于初始位置 时,点D与C重合(如图②).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.已知太阳光线与地面的夹角为 (如图③),为使遮阳效果最佳,点P需从 上调多少米?(结果精确到 )(参考数据: , , )

 24. 如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端 处竖直立一根长1.72米的木棒 ,并测得此时木棒的影长 米;然后小夏在 的延长线上找出一点 ,使得 、 、 三点在同一直线上,并测得 米已知图中所有点均在同一平面内, , ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度 .
24. 如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端 处竖直立一根长1.72米的木棒 ,并测得此时木棒的影长 米;然后小夏在 的延长线上找出一点 ,使得 、 、 三点在同一直线上,并测得 米已知图中所有点均在同一平面内, , ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度 . 25. 随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长。(结果保留根号)
25. 随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长。(结果保留根号) 26. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
26. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.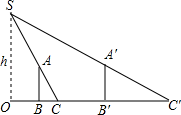 27. 西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为 ,测得教学楼楼顶点C处的俯角为 .又经过人工测量得到操控者和教学楼 的距离为57米,求教学楼BC的高度.(注:点 都在同一平面上,无人机大小忽略不计.参考数据: )
27. 西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为 ,测得教学楼楼顶点C处的俯角为 .又经过人工测量得到操控者和教学楼 的距离为57米,求教学楼BC的高度.(注:点 都在同一平面上,无人机大小忽略不计.参考数据: ) 28. 如图,某路灯在铅垂面内的示意图,灯柱AB的高为13米,灯杆BC与灯柱AB的夹角∠B=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为20米,已知tan∠CDE=
28. 如图,某路灯在铅垂面内的示意图,灯柱AB的高为13米,灯杆BC与灯柱AB的夹角∠B=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为20米,已知tan∠CDE= ,tan∠CED= ,求灯杆BC的长度.
,tan∠CED= ,求灯杆BC的长度.  29. 如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
29. 如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1; ≈1.4)
 30. 如图,在建筑物顶部有一长方形广告牌架 ,已知 ,在地面上A处测得广告牌 上端 的仰角为 ,且 ,前进 到达B处,在B处测得广告牌架下端D的仰角为 ,求广告牌 架下端D到地面的距离.
30. 如图,在建筑物顶部有一长方形广告牌架 ,已知 ,在地面上A处测得广告牌 上端 的仰角为 ,且 ,前进 到达B处,在B处测得广告牌架下端D的仰角为 ,求广告牌 架下端D到地面的距离. 31. 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据: ≈1.4, ≈1.7)
31. 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据: ≈1.4, ≈1.7) 32. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹标顶端离地面2.4m,小明到竹杆的距离DF=2m,竹杆到塔底的距离DB=32m,求这座古塔的高度.
32. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹标顶端离地面2.4m,小明到竹杆的距离DF=2m,竹杆到塔底的距离DB=32m,求这座古塔的高度.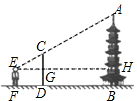 33. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 平行于水平地面 的一个平台.小华想利用所学知识测量古塔的高度 她在平台的点 处水平放置--平面镜,并沿着 方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知 请你根据题中提供的相关信息,求出古塔的高度 .(参考数据: )
33. 某公园有一座古塔,古塔前有一个斜坡 坡角 ,斜坡高 米, 平行于水平地面 的一个平台.小华想利用所学知识测量古塔的高度 她在平台的点 处水平放置--平面镜,并沿着 方向移动,当移动到点N时,刚好在镜面中看到古塔顶端点 的像,这时,测得小华眼睛与地面的距离 米, 米, 米, 米,已知 请你根据题中提供的相关信息,求出古塔的高度 .(参考数据: ) 34. 西安市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为30°,然后向教学楼正方向走了5米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°。已知教学楼高BM=16米,且点A,B,M在同一直线上,求宣传牌AB的高度。(结果保留根号)
34. 西安市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为30°,然后向教学楼正方向走了5米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°。已知教学楼高BM=16米,且点A,B,M在同一直线上,求宣传牌AB的高度。(结果保留根号) 35. 大雁塔南广场玄奘铜像是为纪念唐代高僧玄奘而设计.在一次课外活动中,甲、乙两位同学测量玄奘铜像的高度他们分别在A,B两处用高度为1.8m的测角仪测得铜像顶部C的仰角分别为30°,60°,两人间的水平距离AB为10m,求玄奘铜像的高度CF.(结果保留根号)
35. 大雁塔南广场玄奘铜像是为纪念唐代高僧玄奘而设计.在一次课外活动中,甲、乙两位同学测量玄奘铜像的高度他们分别在A,B两处用高度为1.8m的测角仪测得铜像顶部C的仰角分别为30°,60°,两人间的水平距离AB为10m,求玄奘铜像的高度CF.(结果保留根号) 36. 如图,在△ABC中,AB=8,BC=4,CA=6,CD//AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
36. 如图,在△ABC中,AB=8,BC=4,CA=6,CD//AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.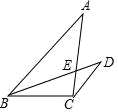 37. 如图1所示的是宝鸡市文化景观标志“天下第一灯”,它由国际2.0不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分4层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部O,他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点A,并在点A处安装了测量器AB,在点B处测得该灯的顶点P的仰角为 ;再在OA的延长线上确定一点C,使 米,在D点处测得该灯的顶点P的仰角为 .若测量过程中测量器的高度始终为1.6米,求“天下第一灯”的高度. ,最后结果取整数)
37. 如图1所示的是宝鸡市文化景观标志“天下第一灯”,它由国际2.0不锈钢板整体锻造,表面涂有仿古金色漆,以仿青铜纹饰雕刻的柱体四盏灯分4层布置.一天上午,数学兴趣小组的同学们带着测量工具来测量“天下第一灯”的高度,由于有围栏保护,他们无法到达灯的底部O,他们制定了一种测量方案,图2所示的是他们测量方案的示意图,先在周围的广场上选择一点A,并在点A处安装了测量器AB,在点B处测得该灯的顶点P的仰角为 ;再在OA的延长线上确定一点C,使 米,在D点处测得该灯的顶点P的仰角为 .若测量过程中测量器的高度始终为1.6米,求“天下第一灯”的高度. ,最后结果取整数) 38. 某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
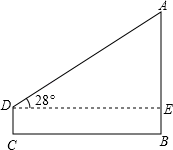
38. 某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
四、作图题

